高次Haar函数的推广*

陈 伟，蔡占川

(1. 江南大学数字媒体学院, 江苏 无锡 214122；2. 澳门科技大学资讯科技学院, 澳门)

高次Haar函数的推广*

陈 伟1，蔡占川2

(1. 江南大学数字媒体学院, 江苏 无锡 214122；2. 澳门科技大学资讯科技学院, 澳门)

k次V-系统是一类正交分段多项式函数系,Haar函数是当k=0时的情形, 因而又称为高次Haar函数。V-系统定义在区间[0,1]上的均匀剖分上, 经过对所谓“生成元函数”进行2n倍压缩及平移得到。提出了一种正交非均匀分段多项式函数系的构造方法, 称之为高次非均匀Haar函数系。对于任意给定的区间[0,1]上的非均匀层次嵌套剖分, 首先定义一组截断单项式，并证明了对这组截断单项式系进行Gram-Schmidt过程, 结果便是相应的高次非均匀Haar函数, 原来的V-系统只是高次非均匀Haar函数系的特殊情形。证明了该函数系的正交性, 再生性及收敛性, 并给出了一个具体构造实例。

V-系统；Haar函数；非均匀；Gram-Schmidt

正交变换在信号逼近、 压缩、 特征提取等领域具有广泛的应用, 它的数学基础便是正交函数系[1-3]。在众所周知的Fourier三角函数系以及诸多正交多项式系中, 每一个基函数不仅是连续的, 而且具有任意阶的连续导数。 历史上, 为了回答“是否存在非连续的完备正交函数系”这样的反问, 匈牙利数学家Haar构造了后人称呼的“Haar函数”。如果不考虑规范系数, Haar函数仅取值+1,-1或0, 因此可以看作是一类正交零次分段多项式函数系。当小波分析兴起后,Haar函数成为小波变换中典型的波函数代表[1]。

2007年, 国内学者宋瑞霞等[4]构造了一类L2[0,1]上的完备正交分段多项式函数系, 称为k(k=0,1,2,…)次V-系统,V-系统是一类有限区间上的正交多小波[5],Haar函数是k=0时的特殊情形, 因此V-系统又称为高次Haar函数[6]。与传统的连续正交函数不同,V-系统既包含光滑函数, 又有各个层次的间断函数, 从而能够表达更加复杂的信号。文献[7-9]将V-系统应用到几何图形表达, 数据聚类, 三维模型重构与检索等实际问题中, 取得了良好的结果。

V-系统是通过对所谓“生成元函数”作2n(n=1,2,…)倍压缩得到, 这种构造方式建立在区间[0,1]的均匀剖分基础上, 因而基函数的分段点位置只出现在q/2p处。本文的目的, 是构造非均匀剖分节点下的V-系统, 称之为非均匀高次Haar函数。

当分段节点位置为非均匀分布时, 原来的V-系统构造方法不再有效。 也就是说, 不再能够通过压缩与平移操作得到。本文提出了一种高次非均匀Haar函数系的构造方法, 根据给定的区间[0,1]上的非均匀层次嵌套分割, 首先定义一类线性无关函数系。本文证明, 对这类线性无关函数系作Gram-Schmidt正交化手续, 结果便是对应非均匀节点分割上的高次Haar函数系, 原来的均匀V-系统只是它的一种特殊情形。进一步地, 本文从理论上证明了高次非均匀Haar函数系的正交性, 再生性及收敛性。

1 V-系统

V-系统是一类正交分段多项式函数系, 其中既包含连续的基函数, 又包含具有各种层次间断性的基函数。因此V-系统能够兼顾Fourier三角基与Haar函数的优点, 可以更好地表达信号。

其中

[f,g]

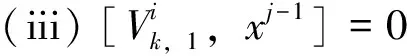
从第2组(n=2)开始，V-系统中的基函数均由生成元经压缩及平移直接得到，如下：

那么, 函数集合

即为k次V-系统。

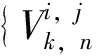
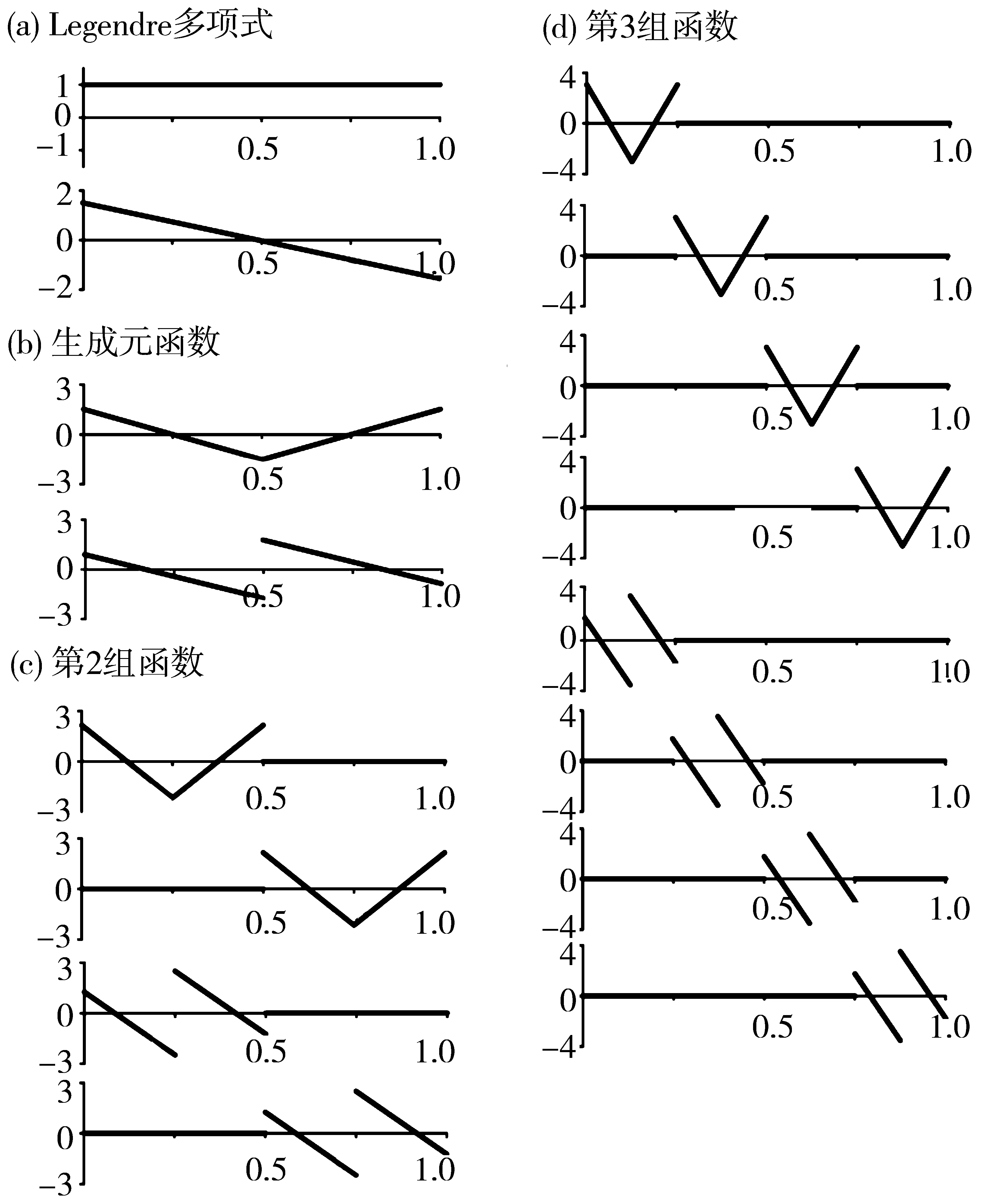
图1 均匀V-系统前10项基函数(k=1)Fig.1 The first 10 base functions of uniform V-system (k=1)

2 高次非均匀Haar函数

2.1 非均匀层次嵌套分割

Haar函数及V-系统定义在区间[0,1]的自相似均匀分割上。本文构造的高次Haar函数系, 同样定义在一个具有层次嵌套关系的分割上。不同的是，各层的分割位置不再固定为q/2p处。

定义2 (非均匀层次嵌套分割)

为区间[0,1]上的第n层非均匀剖分, 满足如下条件：

(iv)Jn=2n;

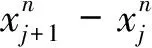
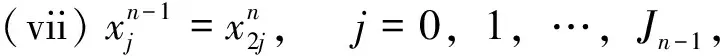
图2所示为当n=0,1,2,3,4时的某一组非均匀层次嵌套分割。

图2 区间[0,1]上的非均匀层次嵌套分割Fig. 2 Non-uniform hierarchical nested partition in the interval [0,1]

2.2 截断单项式

本文构造的高次非均匀Haar函数系, 由于失去了原有自相似均匀剖分的特点, 不再能够直接通过生成元函数得到整个函数系。因此，首先定义一类截断单项式函数系。

称为Xn上的截断单项式函数系。

2.3 高次非均匀Haar函数

证明 按截断单项式函数系中的函数按序排列并记为W1,W2,…,Wj,…, 相应的正交化结果记为G1,G2,…,Gj,…, 而将k次非均匀Haar函数系记为V1,V2,…,Vj,…。

当j=1时, 可具体验证G1=W1=V1。

当j=2时, 可具体验证G2=W2=V2。

假定Gj=Vj对j=1,2,…,m-1(m≥4)成立, 根据Gram-Schmidt正交化手续,

下面将证明上述事实对j=m也成立。

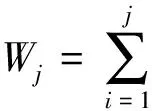
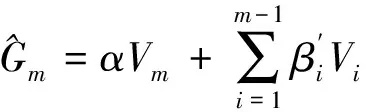
证毕。

2.4 性质

定理2(标准正交性)k次非均匀Haar函数系是L2[0,1]上的标准正交函数系, 即

证明 根据定理1,k次非均匀Haar函数系由线性无关函数组经Gram-Schmidt正交化手续得到, 从而得证。

定理3(再生性) 设f(x)是区间[0,1]上的分段k次多项式, 且分段点位于Xn{0,1}, 则f(x)可以用Xn上的k次非均匀Haar函数系的有限项基函数线性组合精确表示，即

其中Λ为有限的指标集。

证明 根据定义2, 记Xn分割之下的分段k次多项式集合为Pk,Δn, 则

因而

此即说明,Xn分割之下任一分段k次多项式都可以由k次非均匀Haar函数系的前2n(k+1)个基函数精确表达。证毕。

假设f(x)是给定的函数, 定义

为函数f(x)的非均匀Haar级数, 其中

记

为函数f(x)的非均匀Haar级数的部分和。那么, 有下面的定理。

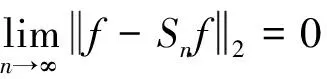
另一方面,l(x)∈Pk,Δn, 即表明对于f(x)∈L2[0,1]来说, 存在h(x)∈Mk,n, 使得

定理3表明本文构造的高次非均匀Haar函数系是L2[0,1]中的完备正交函数系[11]。

3 例 子

定理1从理论上给出了高次非均匀Haar函数系的构造方法，这里以一个具体例子进行验证。

给定如下非均匀层次嵌套分割X3, 通过本文方法, 构造出相应的高次非均匀Haar函数系。

运用本文方法, 可以得到任意k次的非均匀Haar函数系。 限于篇幅, 这里只列出该非均匀分割上的1次与2次Haar函数系的基函数图像, 见图3与图4, 并列出1次非均匀Haar函数的前8项基函数表达式。

n=0:

n=1:

n=2:

图3 非均匀高次Haar函数(k=1)Fig.3 The high order non-uniform Haar functions (k=1)

图4 非均匀高次Haar函数(k=2)Fig.4 The high order non-uniform Haar functions (k=2)

4 结 论

现有的正交分段多项式函数系定义在有限区间的均匀分割上, 本文构造了一类非均匀正交分段多项式函数系, 称之为高次非均匀Haar函数系。传统的V-系统是它的一种特殊情形。根据给定的非均匀层次嵌套分割, 根据本文方法, 可以自动高效地得到相应的任意k次非均匀Haar函数系, 并且该函数系具有正交性, 再生性及收敛性。

[1] 齐东旭, 宋瑞霞, 李坚. 非连续正交函数—U-系统、V-系统、多小波及其应用[M]. 北京：科学出版社, 2011.

[2] 杨发权, 李赞, 罗中良，等. 一种N维数据块正交调制及其调解识别方法的研究[J]. 中山大学学报(自然科学版), 2012, 52(5): 18-22.

[3] 蔡占川, 陈伟. 基于正交GF系统的散乱数据拟合及分析[J]. 中山大学学报(自然科学版), 2013, 51(3): 73-77.

[4]SONGRX,MAH,WANGTJ,etal.CompleteorthogonalV-systemanditsapplications[J].CommunicationsonPureandAppliedAnalysis, 2007, 6(3): 853-871.

[5]HUANGC,YANGLH,QIDX.Anewclassofmulti-waveletbases:V-system[J].ActaMathematicaSinica, 2012, 28(1): 105-120.

[6] 熊刚强, 齐东旭. 高次Walsh系与高次Haar系[J]. 宁夏大学学报(自然科学版), 2011,32(2): 109-115.

[7] 宋瑞霞, 王也娜, 李成华，等.V-系统在形状相似检索中的应用[J]. 计算机辅助设计与图形学学报, 2014, 26(11): 1930-1937.

[8]SONGRX,ZHAOZX,WANGXC,etal.AnapplicationoftheV-systemtotheclusteringofChernofffaces[J].ComputersandGraphics, 2010, 34: 529-536.

[9]SONGRX,YAODX,WANGXC,etal.Retrievalmethodfor3DobjectgroupbasedonV-system[J].JournalofAdvancedMechanicalDesign,Systems,andManufacturing, 2012, 6(3): 340-353.

[10] 徐森林. 实变函数论[M]. 合肥：中国科学技术大学出版社,2013.

[11]BOORCD.Apracticalguidetothesplines(revrisededition)[M].NewYork:Springer-Verlag, 2001.

The generalization of high order Haar functions

CHENWei1,CAIZhanchuan2

(1. School of Digital Media, Jiangnan University, Wuxi 214122, China;2. Faculty of Information Technology, Macau University of Science and Technology, Macau, China)

ThekdegreeV-systemisaclassoforthogonalpiecewisepolynomialfunctionswhichisalsonamedashighorderHaarfunctions.V-systemisdefinedontheuniformpartitionofinterval[0,1]andobtainedbymulti-scalesqueezingandshiftingoperationsontheso-calledgenerators.TheV-systemtothecaseofnon-uniformpartitionisgeneralized,andthecorrespondingresultisnamedashighordernon-uniformHaarfunctions.Foranygivenpartitionontheinterval[0,1],asetoftruncatedmonomialswasfirstlydefined.Itisprovedthatthenon-uniformHaarfunctionscanbeobtainedthroughtheGram-Schmidtorthogonalizationprocess.Theorthogonality,reproducibilityandconvergenceoftheproposedfunctionsareproved,andaspecificconstructiveexampleisalsogiven.

V-system; Haar functions; non-uniform; Gram-Schmidt

10.13471/j.cnki.acta.snus.2016.03.010

2015-07-07

国家自然科学基金资助项目(61402201)；澳门科技发展基金资助项目(110/2014/A3)；浙江大学CAD&CG国家重点实验室开放课题资助项目(A1513，A1609)；中央高校基本科研业务费资助项目(JUSRP11416)

陈伟(1986年生)，男；研究方向：信号处理;E-mail:chenwei.must@gmail.com

TP

A

0529-6579(2016)03-0059-05