立体视觉双目图像MAP的优化复原方法

洪汉玉，范　艳，时　愈，华　夏，张天序

(1.武汉工程大学电气信息学院，湖北 武汉，430205；2.华中科技大学多谱信息处理技术国家级重点实验室，湖北 武汉，430074)

立体视觉双目图像MAP的优化复原方法

洪汉玉1，范艳1，时愈1，华夏1，张天序2

(1.武汉工程大学电气信息学院，湖北 武汉，430205；2.华中科技大学多谱信息处理技术国家级重点实验室，湖北 武汉，430074)

摘要：为了有效地对立体视觉双目模糊图像进行复原，提出一种动目标双目图像MAP的优化复原方法，将双目运动模糊图像的复原问题转化为在模糊核路径关系约束下的双重循环MAP优化估计问题，在保证模糊核路径对应关系前提下，对双目图像进行去模糊。建立了双目图像模糊核路径的对应关系模型，将关系模型作为约束条件式，嵌入到基于模糊核和双目原图像的MAP优化估计过程中，通过双重循环迭代获取双目图像的模糊核和清晰图像。实验结果表明，该方法能够有效地去除立体视觉双目图像的模糊。

关键词：立体视觉；动目标；双目图像； MAP；模糊核；图像复原

在计算机视觉系统中，由于单观测点图像不能为目标识别和监控提供有效的三维信息，所以目前计算机视觉系统通常需要同步采集两个观测点图像。而在短曝光时间内，观测目标与成像系统之间存在相对运动，导致采集到的观测图像是模糊的，图像质量一般较差。因此，为了获得完整的三维信息，实际工作中往往需要解决短曝光双目视觉系统中动目标图像复原的问题。

目前动目标图像复原方法主要有单帧图像复原法[1-2]和多帧图像复原法[3], 其中单帧图像复原法基于单个相机采集的单帧图像进行复原，复原效果仅对同一视角的模糊图像有效；而多帧图像复原法去模糊效果较好，但有如下的限制条件：同一视角、同一场景，且需要较多的先验知识，适用范围较窄。因此，基于混合图像系统的图像复原方法应运而生[4-5]。在混合图像系统中，虽然相机采集到的图像是两个不同视角的观测图像，但该方法仅利用其中一个视角的观测图像信息对另一个视角的图像进行复原。以上方法并未考虑观测图像之间的像素位置关系，因而均不适用于解决双目视觉系统中图像的复原问题。为此，本研究提出一种双目观测图像最大后验估计(MaximumAPosteriori,MAP)优化复原方法，在立体视觉系统中，建立双目模糊核路径的对应关系数学模型，并对两个模糊核路径对应关系进行优化处理，通过双重循环迭代地估计双目模糊核和清晰图像。

1立体视觉双目图像的运动模糊形成机理

立体视觉系统中，三维(3D)空间中目标的运动路径投影如图1所示。短曝光时间内，在3D空间中，当物体从P运动到Q，映射到观测面上，对应运动Mi(t)从pi运动到qi(i=1,2)，不同观测面上成像视点的位置和角度是不同的，使得每个观测面上piqi的长度和方向也不同。观测图像gi(x,y)可以表示如下：

(1)

式中：hi(x,y)、fi(x,y)及ni(x,y)分别表示模糊核、清晰图像和噪声；⊗表示2D离散卷积；下标i为观测点标号。

图像模糊是由目标在空间中的运动引起的。在短曝光时间内，由于动目标在不同时刻的空间位置是不同的，所以，动目标在双目左右两个成像面上的投影是不一样的。从光学理论上讲，图像模糊可看成动目标在成像积分时间内的运动影像积累。因为在左右两个像平面动目标影像的投影是不一样的，动目标影像积累及运动轨迹也不一样，因此两个像平面内双目图像的模糊核及模糊路径是不同的。

图1　立体视觉双目运动路径对应关系示意图

Fig.1 The correspondence between motion paths in the binocular stereo vision system

2双目模糊核路径的关系模型

双目立体视觉两个观测面的模糊核路径对应3D空间中同一运动路径。因此，两个投影模糊核路径之间存在对应关系。模糊核可以由线段或平滑的曲线段近似表示[3]。对于双目立体视觉系统中的运动模糊图像复原，要迭代地估计两个投影模糊核路径，确保估计的投影模糊核路径保持对应关系。

2.1模糊核路径的关系

考虑目标的线性运动，令相机参数映射矩阵为P ；(xyz1)为3D齐次坐标系中的一点，映射到2D观测面上，则(u v 1)为 2D坐标系中的一点，那么(x y z 1)和(u v 1)的对应关系如下：

(2)

式中：d为相机的景深。

相机参数映射矩阵P可定义为K*[Rt]，其中相机参数矩阵K和[Rt]可在相机标定的过程中计算得到。

从式(1)和图1可知，每个观测面的模糊核路径是不同的。为简化计算，假设运动模糊核路径是空间不变的。当物体在空间中从P点运动到Q点, 映射到两个观测面上分别为p1q1和p2q2,如图2所示。相机参数映射矩阵P是可逆的，通过式(2)，可以从(u,v)和d推导得到(x,y,z)，如下式所示：

(3)

其中：

(4)

(a) 观测面1(b) 观测面2

图2三维立体空间中运动piqi在两个观测面上的投影

Fig.2 Movement projection of piqion two observed imaging planes of 3D space

(5)

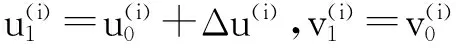
(6)

双目立体视觉系统中，两个观测面上的点对(Δu(1),Δv(1))和(Δu(2),Δv(2))是相关的，那么一定满足式(6)的关系，因此可以利用式(6)来检查点对是否相关。

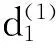
2.2离散化后的模糊核路径的对应关系

物体沿着空间路径运动，在每个观测面投影，对应沿着投影路径运动。不同观测面的投影路径不同。必须注意的是，对空间路径上的任意一点，投影到观测面，对应两个模糊核路径上的点对(u(1)，v(1))和(u(2),v(2))。通过对模糊核支撑域沿着轨迹(模糊路径)离散化，可建立模糊核路径之间的关系：uk=u0+Δuk,vk=v0+Δvk(k=0,1,…,N-1)，其中k为沿着运动轨迹的离散点序号。

两个观测面上离散化的模糊核路径上的点对是对应的，对应的点对是3D空间上同一个点的投影。类似于式(6)中模糊核路径之间的关系，这里扩展两个观测面上离散化的模糊核路径上离散点对的关系，离散化后的模糊核路径如图3所示。由图3中可知：

(a) 观测面1

(b) 观测面2

图3两个观测面上离散化的模糊核路径

Fig.3 Discretization of blur kernel paths on two observed imaging planes

3图像复原优化框架

3.1MAP优化

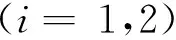
(7)

式中：P(gi|fi,hi)表示在已知原始图像fi(x)和模糊核hi(x)的前提下，模糊图像gi(x)产生的概率；P(fi)和P(hi)分别表示原始图像和模糊核的先验概率。

由于观测到的模糊图像、原始图像和模糊核可以视为是独立分布的，故可建立如下的MAP估计框架：

(8)

最大后验概率对原图像和模糊核的估计，可以通过极小化条件概率密度函数P(fi,hi|gi)的非负对数函数获得：

(9)

其中，

L(fi,hi|gi)=-log(P(fi,hi|gi))

(10)

由式(7)、式(8)可得：

(11)

将P(fi)和P(hi)的非负对数记为L(fi)和L(hi)。在实际情况下，观测到的模糊图像往往受到噪声的干扰，一般可假定每像元噪声服从泊松分布，那么观测图像的概率密度函数可以表示为

(12)

对式(12)取对数，并去掉常数项，可以得到：

(13)

图像复原是一个不适定问题，为了提高图像复原的稳定性并抑制噪声干扰，可以采用一些正则化技术。由于相邻点相关，最小化它们的差异可以视为对空间相关性的约束，构造如下正则化项[6]：

(14)

将式(14)合并到式(13)可得：

(15)

(16)

同理，对L(fi,hi|gi)取关于hi的导数并令其为零，模糊核可以通过如下公式迭代更新：

(17)

3.2目标图像估计过程

(18)

3.3模糊核估计过程

(19)

式中：下标m表示内循环次数。

在原图像和模糊核估计过程中，分别进行M1和M2次迭代。当两个内循环迭代结束以后，再进行下面的模糊核的优化处理。

3.4双目模糊路径坐标对应关系的优化处理

(20)

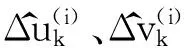
对双目观测点图像的模糊核路径对应关系进行优化处理，然后将优化以后的模糊核用于目标图像恢复的迭代过程中，直到满足迭代终止条件为止。经过几次迭代以后，即可得到满足双目模糊核路径对应关系的模糊核和双目复原图像。

3.5双目图像复原算法流程图

本文提出的算法主要包括以下流程：设置目标图像和模糊核的初始值，在两个内循环中估计目标图像和模糊核，对估计出来的双目模糊核路径进行优化处理，将优化后双目模糊核进行外部循环，直到满足终止条件为止。算法流程图如图4所示。

Fig.4 Flow chart of image restoration calculation in the binocular system

4仿真及实验验证

为验证本研究的算法，采用VC++6.0编程，在Dell计算机(2.67 GHz CPU,4 GB内存)上运行，对双目图像进行去模糊效果测试。

以双目相机采集固定不动目标的双目图像作为基准图像(原图像，图像大小为1024×1024像素)进行仿真，对本研究算法与目前图像复原效果较好的Shan方法进行比较，结果如图5所示。由图5中可知，本研究方法比Shan方法估计的模糊核路径要精细一些。

以图5中原图像为基准，分别计算模糊图像、Shan方法恢复图像及本研究方法恢复图像的归一化均方差值(Normalized Mean Squared Error，NMSE)，计算结果如表1所示。从表1可知，本研究方法得到的NMSE值最小，表明采用本研究方法恢复后的图像与原图最接近，图像恢复效果好。

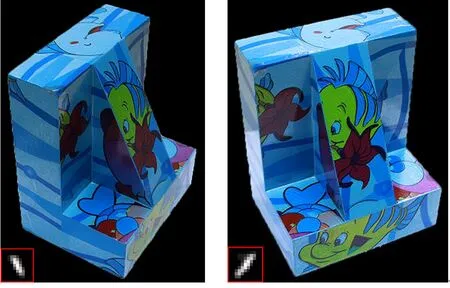
图6所示为一组实际双目图像复原及视觉对比实验的结果，下方小图为大图中对应方框内局部图的2.5倍放大图)。由图6中可以看出，采用Shan方法对左、右视点图像分别进行恢复，恢复结果有显著振铃效应；而采用本研究方法恢复的结果振铃效应明显减少，恢复的图像清晰度高、视觉效果较好。局部放大图的细节对比也表明本研究方法能够获得更好的恢复效果。

图4　双目图像复原算法流程图

(a) 原图像

(b) 运动模糊图像

(c) Shan方法恢复的图像

(d) 本研究方法恢复的图像

Fig.5 Restoration for simulated motion blurred binocular images

表1　NMSE值对比

(a) 实际运动模糊的双目图像

(c) 本研究方法恢复的双目图像

Fig.6 Restoration of real motion blur binocular images

5结语

在双目相机同步采集情况下，本研究提出了双目图像MAP的优化复原方法，将双目图像的复原问题转化为在模糊核路径关系约束下的双重循环MAP优化估计问题。建立了两个观测图像模糊路径之间的对应关系模型，将关系模型作为约束条件式，嵌入到基于模糊核和双目原图像的MAP优化估计过程中，有效地恢复双目模糊图像。实验结果表明本研究的方法对双目模糊图像的复原能够获得较好结果。

参考文献

[1]Xiao L, Gregson J, Heide F, et al. Stochastic blind motion deblurring[J]. IEEE Transactions on Image Processing, 2015, 24(10):3071-3085.

[2]Shan Q, Jia J Y, Agarwala A. High-quality motion deblurring from a single image[J].ACM Transactions on Graphics, 2008, 27(3):Article 73.

[3]Hintermüller M, Wu T. Bilevel optimization for calibrating point spread functions in blind deconvolution[J].Inverse Problems and Imaging,2015,9(4):1139-1169.

[4]Ben-Ezra M, Nayar S. Motion-based motion deblurring[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(6):689-698.

[5]Tai Y W, Du H, Brown M S, et al. Correction of spatially varying image and video motion blur using a hybrid camera[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(6):1012-1028.

[6]Hong H Y, Park I K. Single-image motion deblurring using adaptive anisotropic regularization[J]. Optical Engineering, 2010, 49(9):097008.

[责任编辑郑淑芳]

Method for MAP optimization image restoration in binocular stereo system

HongHanyu1,FanYan1,ShiYu1,HuaXia1,ZhangTianxu2

(1.School of Electrical and Information Engineering, Wuhan Institute of Technology, Wuhan 430205,China；2.National Key Laboratory of Science and Technology on Multi-spectral Information Processing,Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:In order to remove the motion image blurring in binocular stereo vision system effectivery, this paper presents a novel motion image restoration method based on MAP optimization. The problem of motion blurry binocular image restoration can be transformed into MAP optimization and estimation double loop problem within the constraint of the relationship of blur kernel paths. The binocular image deblurring is performed under the condition that the corresponding relationship of blur kernel paths is guaranteed.The corresponding relationship model of motion blur kernel paths for the binocular image is built, and embedded into MAP optimization estimation as the constraints. The clear image and blur kernel of the binocular image is obtained by double circulation iteration.Experimental results show that the proposed approach is effective to deblur the binocular image in the stereo vision system.

Key words：stereo vision; moving object; binocular images; MAP; blur kernel; image restoration

收稿日期：2015-12-20

基金项目：国家自然科学基金面上项目(61175013)；湖北省自然科学基金创新群体项目(2012FFA046).

作者简介：洪汉玉(1964-)，男，武汉工程大学教授，博士生导师.E-mail:hhyhong@163.com

中图分类号：TP391.41

文献标志码：A

文章编号：1674-3644(2016)01-0062-07