超声椭圆振动切削装置的运动学建模与实验验证
史桂林,张 臣
(南京航空航天大学机电学院,江苏 南京,210016)
超声椭圆振动切削装置的运动学建模与实验验证
史桂林,张臣
(南京航空航天大学机电学院,江苏 南京,210016)
摘要:对一种二维椭圆振动辅助切削(EVC)装置的运动学特性进行分析,建立该装置刀尖轨迹的运动学模型,从理论上探讨该装置刀尖运动在一定激励下产生椭圆轨迹的可能性。同时实际加工出EVC装置,在相应的检测系统下测试该EVC装置的刀尖运动轨迹数据,利用测得的数据对运动学模型进行修正,并将修正后的模型输出值与实测值进行比较,验证了修正后模型的有效性。
关键词:椭圆振动切削;切削加工;运动轨迹;运动学建模;模型修正
近年来,随着航空航天产业的迅速发展,脆性晶体材料、黑色金属材料由于其在极限环境下的优良性能而受到越来越多的关注[1]。然而,这些材料大多属于硬脆材料,存在断裂强度接近于屈服强度及各向异性等特点,使得采用常规加工方法易出现裂纹和凹坑等缺陷,同时高的硬度还会使刀具磨损加剧、寿命缩短,因此,如何实现这类材料的高效加工,是一个亟待解决的难题[2]。椭圆振动切削(Elliptical Vibration Cutting,EVC)因其具有可有效降低切削力和减少切削热及刀具磨损等特点,被广泛认为是一种极具发展前景的切削方法[3-4]。国内外学者已设计出多种EVC装置并用于实验,获得了优良的切削效果[1,5-6]。但是,EVC过程中刀具的运动机理目前尚未能得到有效揭示,这制约了最优切削过程的提出。为此,本文通过对一种EVC装置进行运动学分析,建立其刀尖轨迹的运动学模型,采用实验数据对模型进行修正,并验证该模型在预测刀尖运动轨迹方面的有效性。
1EVC原理
EVC加工一般是通过在刀具的切削方向和切深方向输入一定周期的激励信号,经合成后刀具运动轨迹即变成椭圆形状,在切削过程中刀具的椭圆运动使其与工件和切屑周期性地接触、分离,最终达到材料去除的目的。以图1为例说明EVC的加工原理。图1中,加粗椭圆轨迹部分为一个切削周期,其中粗虚线表示的轨迹为刀具与工件分离(即不发生材料切除)的运动过程,粗实线表示的轨迹为刀具与工件接触(即工件材料被刀具切除)的运动过程。在刀具与工件分离的运动过程中,切削热得以散发,切屑与工件和刀具分离,有利于提高工件的表面质量,延长刀具的使用寿命。
2二维EVC装置的运动学建模
2.1运动学分析
图2所示为EVC装置简图[7],图3所示为其刀尖位置的局部放大图。该EVC装置由两个螺栓紧固的超声换能器(分别简称为“杆1”、“杆2”)通过刀架处的柔性铰链连接构成。螺栓用于紧固EVC装置的超声换能器,刀架起到对刀具的夹持和对两个换能器的运动进行合成的作用。当施加在两个换能器上的激励同相时,由于结构的对称性,两个换能器在切削方向的位移相互抵消,刀尖沿切深方向运动;当两个激励反相时,两个换能器沿切深方向的运动将相互抵消,刀尖沿切削方向运动。
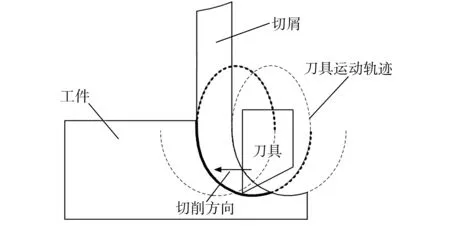
图1 EVC加工原理示意图
Fig.1 Schematic diagram of EVC
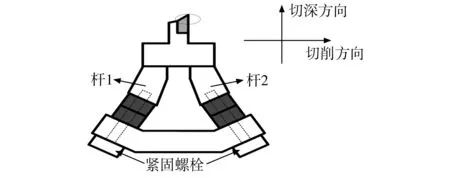
图2 EVC装置简图
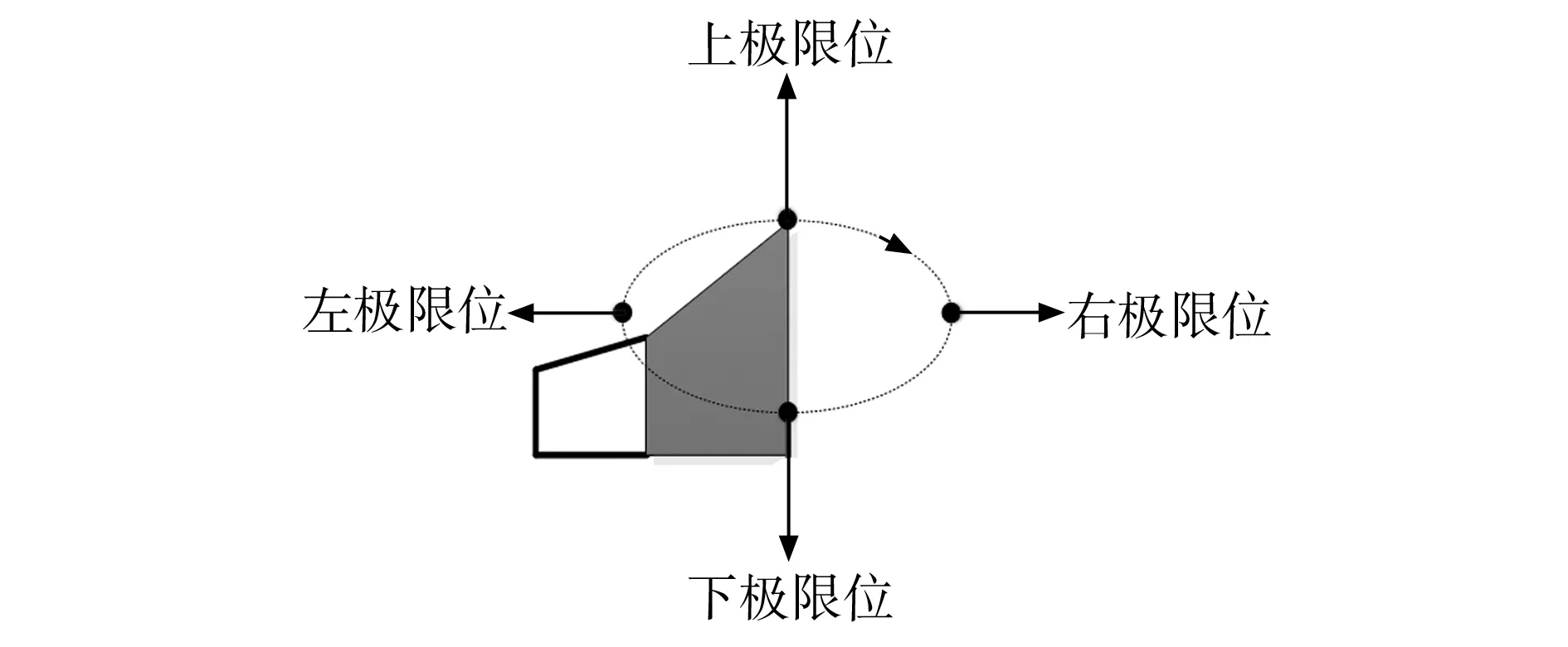
图3 刀尖椭圆轨迹的形成
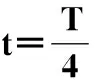
2.2运动学模型的建立
如图4所示,以初始条件t=0(换能器没有任何轴向变形)时两铰链中心连线与刀架中心线的交点o为原点,过o点沿切削方向为ox轴正方向,沿切深方向的反方向为oy轴正方向,建立刀尖椭圆运动轨迹的运动学分析坐标系xoy。PD0为t=0时刀尖顶点的位置;PA0和PB0分别为杆1和杆2靠近铰链处的端点位置;D为PB0( 或PA0) 到ox轴的距离;θ为杆1与杆2之间的夹角;θt为t时刻刀架中心线与ox轴之间的夹角;θD为o点与PD0的连线与刀架中心线之间的夹角,其计算公式如下:
(1)
式中:Ly为刀具厚度;Lx为PD0到oy轴的距离。
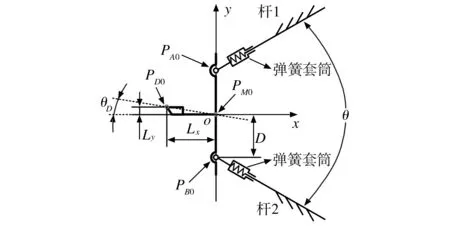
(a)初始时刻
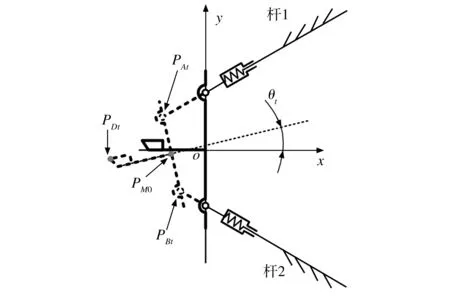
(b)t时刻
以上建立的运动学模型中,t时刻对应的刀尖位置为PDt(pDxt,pDyt),其坐标值可由下式计算:
(2)
式(2)中,(pAxt,pAyt)和( pBxt,pByt)分别为杆1、杆2端点PA和PB在时刻t的坐标值,其中PAt(pAxt,pAyt)点坐标值的计算公式如下:
教育教学改革长期的历史经验告诉我们: 教育目标的达成并非一朝一夕的努力。深度学习的热点研究指向了学生的未来发展、指向了社会的变革动态,具有强大的研究生命力。就本文的主线教学研究而言,一线学科教学中想要促进深度学习的有效达成,应当增加其内涵变式、巧妙结合教学内容,才能够有效指向深度学习发生与否的五大特征。
(3)
PBt(pBxt,pByt)点坐标值的计算方法与此类同。
对于指定结构,L、T、θD均为常量,当杆1和杆2的激励振幅相同、激励相位差为90°时,替换中间变量,刀尖点位置坐标PDt(pDxt,pDyt)可由下式计算:
(4)
式(4)中,因θt远小于θD,故可取-θD≈θt-θD,代入式(4)后将式(4)的上下两式正余弦移至一侧并作平方和计算,可得:
(5)
式(5)即为刀尖运动轨迹的运动学模型。由式(5)中可知,刀尖的理论轨迹是一个标准的椭圆方程。
3实验验证
3.1实验
为验证模型的有效性,以45号钢为材料加工出一套EVC装置进行实验,并采用实验数据对模型进行修正。实验系统简图如图5所示,其中数据采集卡采用NI公司的USB-6361X型采集卡;微位移测量采用MS公司的5300型测量系统,该系统测量的最高频率能达到100 kHz,特别适合高频振动下的检测。
实验时,通过计算机上的LabVIEW程序控制数据采集卡的模拟输出通道生成激励信号,经电压放大器放大后施加在压电陶瓷电极片上。EVC装置受到激励驱动后产生振动,微位移传感器检测刀尖位置并将获得的信号传输到数据采集卡的模拟输入通道,计算机中的LabVIEW程序将采集到的位移数据实时显示并同时以LVM格压电陶瓷在激励电压作用下产生的变形一般主要由两个因素决定:逆压电效应和电致伸缩效应。对于本实验所使用的PZT型压电陶瓷片,电致伸缩效应在激励电压为3000 V以上时才会出现与逆压电效应相当的效果,而本实验中激励电压的幅值仅为350 V,故可忽略电致伸缩效应。压电陶瓷在逆压电效应下产生的位移幅值可由下式计算[8]:
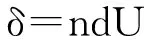
(6)
式中:n为压电陶瓷片的数量;d为压电陶瓷的轴向激励-轴向变形的压电系数,m/V;U为轴向激励电压的幅值,V。
本实验中,换能器上压电陶瓷片在机械上串联,在电路上并联,故n=2;压电陶瓷的压电系数d取为500×10-12m/V,激励电压幅值为350 V,由式(6)计算可得压电陶瓷的位移幅值为:δ=2×350×500×10-12m=0.35×10-6m。
3.2模型计算值与实验实测值的对比
激励电压振幅为350V,激励相位差为90°时的刀尖运动轨迹的运动学模型计算值与实验实测数据的对比如图6所示。图6中,粗实线为对实验数据采用最小二乘法拟合出的运动轨迹,细实线为模型输出数据。由图6中可知,模型计算和实测数据拟合得到的刀尖运动轨迹均为椭圆形,两者在轴长方面的一致性较好,但在椭圆倾斜度方面存在一定差别。这是由于EVC装置在刀架位置处结构的不对称及EVC装置的加工误差导致了振动耦合作用的不均等,引起实际输出与模型输出的椭圆轨迹倾斜方位的不一致。
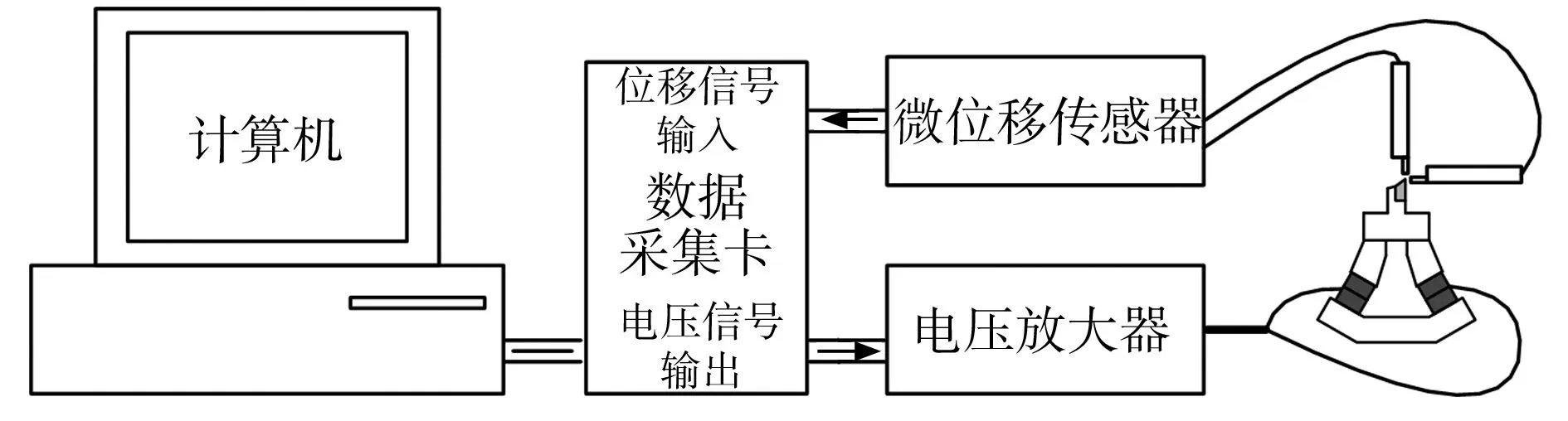
图5 实验系统示意图
Fig.5 Schematic diagram of the experiment system
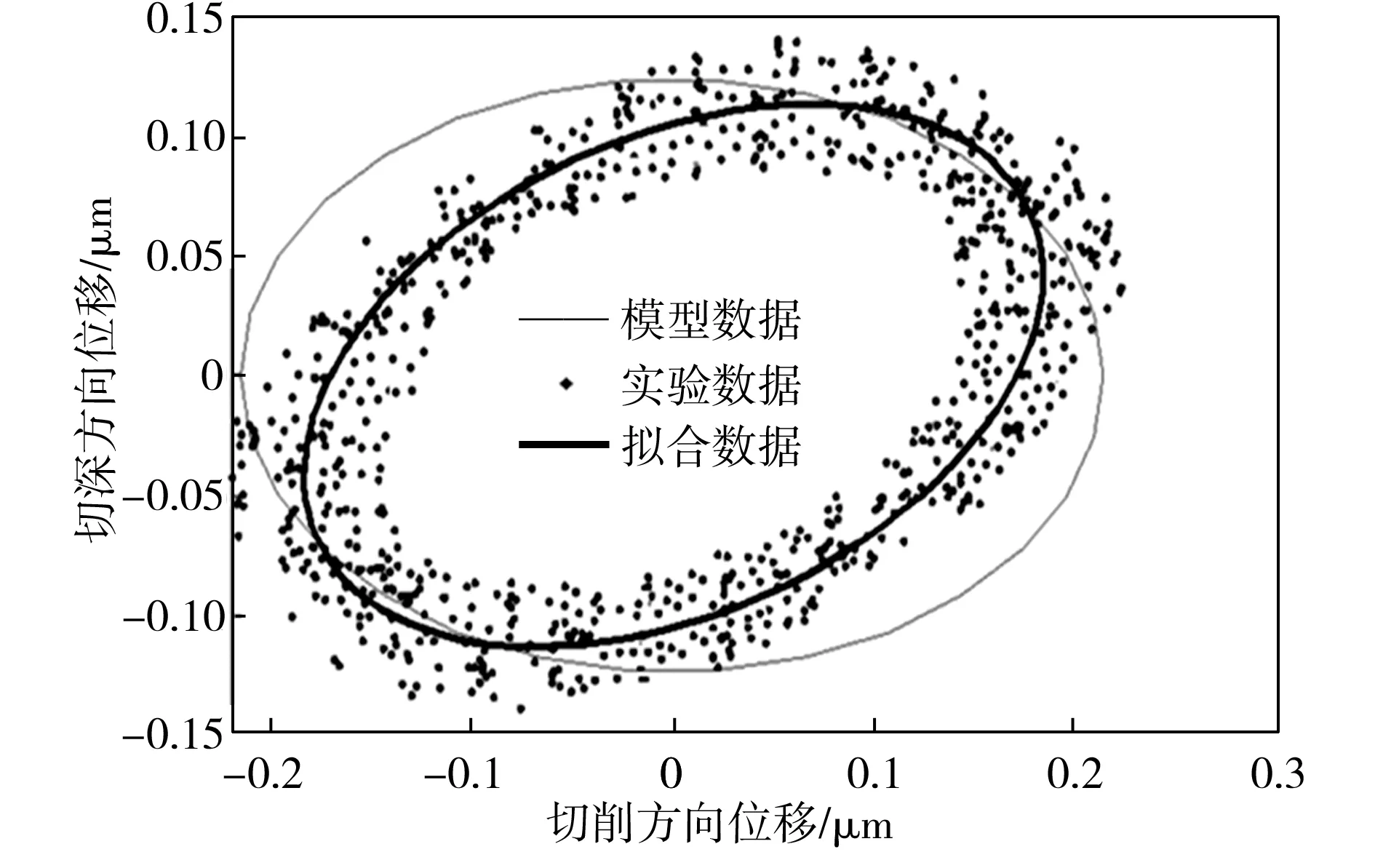
图6 刀尖运动轨迹的模型计算值与实验数据的对比
Fig.6 Comparison between the calculated values and the experimental data for the motion track of the tool tip
3.3模型修正
为提高模型计算的正确性,本文采用实验数据对模型进行修正。
刀尖运动轨迹的模型计算值与实验拟合数据对比如表1所示。模型修正时椭圆轨迹半轴长的补偿将根据补偿系数按比率添加,而倾角(长轴与切削方向的夹角)的补偿则是直接将模型数据按补偿系数旋转至拟合出的角度。表格中拟合数据采用5组重复实验数据,计算误差后取平均值作为最终的补偿系数。
表1模型计算值与实验拟合数据的误差分析
Table 1 Error analysis between the calculated values and the experimental fitting data
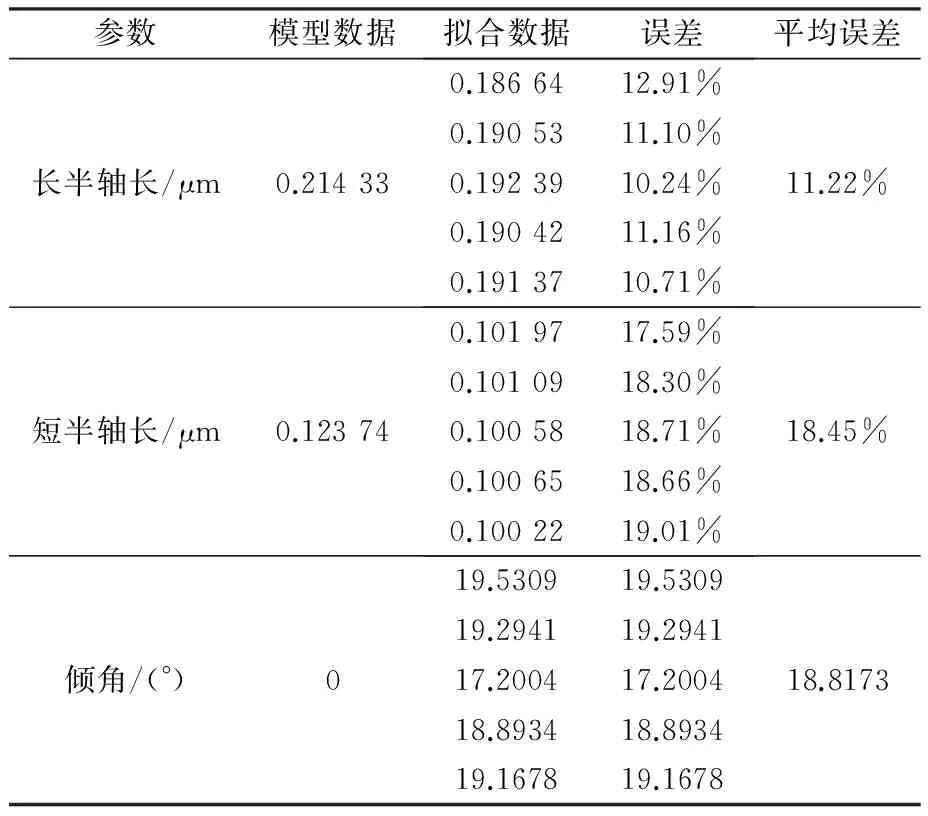
参数模型数据拟合数据误差平均误差长半轴长/μm0.214330.1866412.91%0.1905311.10%0.1923910.24%0.1904211.16%0.1913710.71%11.22%短半轴长/μm0.123740.1019717.59%0.1010918.30%0.1005818.71%0.1006518.66%0.1002219.01%18.45%倾角/(°)019.530919.530919.294119.294117.200417.200418.893418.893419.167819.167818.8173
椭圆轨迹轴长的修正公式如下:
(7)
式中:AXp为模型修正后椭圆半轴长的计算值;AX为模型修正前椭圆半轴长的计算值;RAX为轴长补偿系数,即半轴长的平均误差。
椭圆倾角θp的修正公式为
(8)
式中:θp为模型修正后椭圆倾角的计算值;θE为模型修正前椭圆倾角的计算值;Rθ为倾角补偿系数,即倾角的平均误差。
对修正后的模型进行实验验证,激励电压的振幅为200 V,相位差为90°。修正后模型的计算值与实测数据的对比如图7所示。由图7中可见,修正后的模型计算所得刀尖运动椭圆轨迹的轴长和倾角都与实测数据有较好的一致性,表明修正后的模型能够对EVC装置的刀尖运动轨迹起到准确的预测作用。
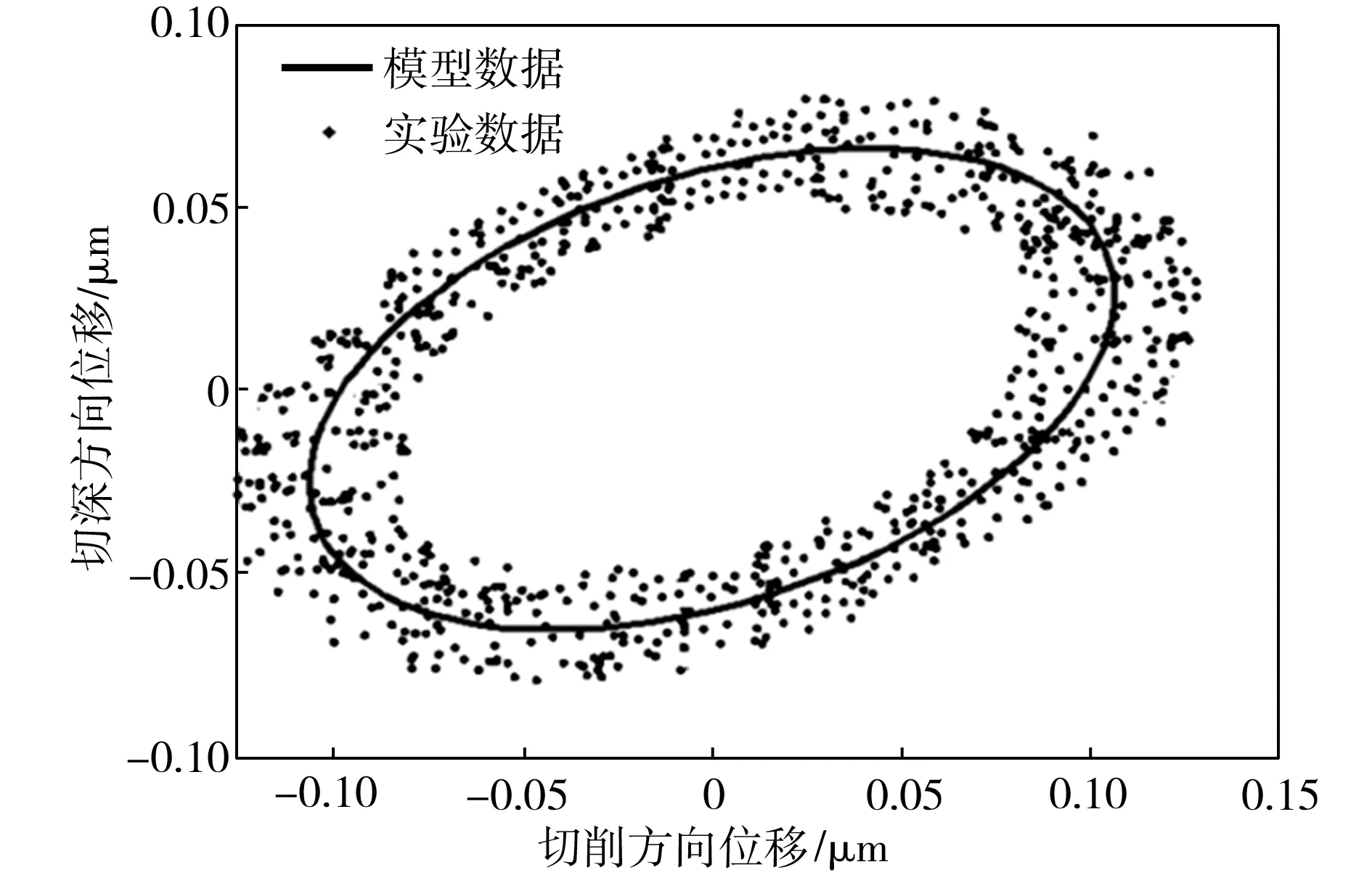
图7 修正后的模型计算值与实验数据的对比
Fig.7 Comparison between the calculated values by modified model and the experimental data
4结语
本文通过对一种EVC装置进行运动学分析,建立了其刀尖运动轨迹的运动学模型,从理论上分析了EVC装置刀尖运动轨迹呈现椭圆形状的可能性。通过实验获得EVC装置刀尖运动轨迹的实测值,并根据实测值对运动学模型进行修正。实验验证结果表明,修正后的模型能有效地预测EVC装置的刀尖运动轨迹。
参考文献
[1]Zhang J,Suzuki N,Wang Y,et al. Fundamental investigation of ultra-precision ductile machining of tungsten carbide by applying elliptical vibration cutting with single crystal diamond[J]. Journal of Materials Processing Technology, 2014, 214(11): 2644-2659.
[2]Hong M S, Ehmann K F. Generation of engineered surfaces by the surface-shaping system[J]. International Journal of Machine Tools and Manufacture, 1995, 35(9): 1269-1290.
[3]Zhang J G, Suzuki N, Kato T, et al. Influence of material composition on ductile machining of tungsten carbide in elliptical vibration cutting[J].Key Engineering Materials,2012, 523: 113-118.
[4]Arif M, Rahman M, San W Y. Analytical model to determine the critical feed per edge for ductile-brittle transition in milling process of brittle materials[J]. International Journal of Machine Tools and Manufacture, 2011, 51(3): 170-181.
[5]Ziki J D A,Didar T F,Wüthrich R. Micro-texturing channel surfaces on glass with spark assisted chemical engraving[J]. International Journal of Machine Tools and Manufacture, 2012, 57: 66-72.
[6]Kim G D,Loh B G. An ultrasonic elliptical vibration cutting device for micro V-groove machining: Kinematical analysis and micro V-groove machining characteristics[J].Journal of Materials Processing Technology, 2007, 190(1): 181-188.
[7]Guo P, Ehmann K F. Development of a tertiary motion generator for elliptical vibration texturing[J]. Precision Engineering, 2013, 37(2): 364-371.
[8]肖彦民.压电驱动型小型精密车床微进给工作台设计[D].焦作:河南理工大学,2012.
[责任编辑郑淑芳]
Establishment and experimental verification of kinematic model of an ultrasonic elliptical vibration-assisted cutting device
ShiGuilin,ZhangChen
(College of Mechanical and Electrical Engineering,Nanjing University ofAeronautics and Astronautics,Nanjing 210016,China)
Abstract:Based on the kinematic analysis, the kinematic model of a 2D elliptical vibration-assisted cutting (EVC) device was established. The elliptical motion locus of the tool tip under certain excitation was theoretically illustrated.The actual EVC device was manufactured and tested by the detecting system, and the kinematic model was modified by the experimental data. The validity of the modified model was verified by the comparison between the calculated values by modified model and the experimertal data.
Key words:elliptical vibration cutting; cutting; motion track; kinematics modeling; model updating
收稿日期:2015-10-13
基金项目:国家自然科学基金资助项目(51575266).
作者简介:史桂林(1991-),男,南京航空航天大学硕士生.E-mail:sglbjb@163.com 通讯作者:张臣(1976-),男,南京航空航天大学副教授,博士.E-mail:meeczhang@nuaa.edu.cn
中图分类号:TH128
文献标志码:A
文章编号:1674-3644(2016)01-0053-05

