关于滤波反投影图像重建算法的研究

李　静

(周口师范学院 数学与统计学院，河南 周口 466001)



关于滤波反投影图像重建算法的研究

李静

(周口师范学院 数学与统计学院，河南 周口 466001)

摘要：CT是投影重建图像的应用技术之一，已广泛应用于自然科学的各领域中.目前CT图像重建算法多采用滤波反投影算法.本文在图像重建的理论基础上，利用滤波反投影算法的基本原理，对R-L, S-L, Hamming滤波函数和新滤波函数分别进行了计算机仿真对比实验. 实验结果表明利用滤波反投影较好地重建图像，关键是滤波函数的选择.

关键词：图像重建；滤波反投影；滤波函数；傅里叶变换；Radon变换

计算机层析成像(Computed Tomography,简称CT)技术是反问题应用的一个典型，在医学诊断、工业产品和无损检测等多个领域有着广泛的应用[1].关于CT图像重建的方法主要有两大类：一类是级数展开法，包括经典的代数重建法(ART)及联合迭代重建法(SIRT)等；一类是变换法，包括滤波反投影算法(FBP,CBP)和直接傅里叶方法等.其中滤波反投影算法是变换法中最常用的，它要求投影数据是完全的，需要用到每一投影方向下的全部数据，因而此算法具有一定的局限性. 但由于滤波反投影算法计算速度快，尽管数据庞大，仍可较快地重建图像，因此，它应用很广泛.

1图像重建的理论基础

1.1物理基础

当X射线束穿过被检测物体时，由于吸收和衍射，X射线会发生衰变.由于物体内部组织的不同，衰减系数μ(x,y)也不同，进而密度函数也不同.若要知道了μ(x,y)的分布，便知道了密度分布.

设强度为I0的单能X射线束穿过某个不均匀物体时，有探测器接收到的X射线强度I服从比尔定律[2]

I=I0·e-∫Lμ(x,y)ds，

其中L是X射线经过的某一路径，上式经过变形可得

称∫Lμ(x,y)ds为射线投影.CT图像重建就是由射线投影来确定物体内部结构.

1.2数学基础

直线L是oxy平面的任意一条直线，t是原点到直线L的距离，则二维Radon变换为[3]

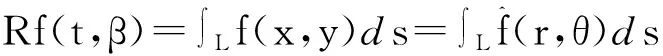
其中(x,y)表示像素点在直角系中的坐标，(r,θ)是像素点(x,y)的极坐标，t,β为直线L的位置参数，f(x,y)表示某一图像密度的二维空间分布.

1.3中心切片定理

由投影重建图像的重要依据是中心切片定理，该定理指出[4]：某图像函数f(x,y)在某一方向上的投影函数Rf(t,β)=Rfβ(t)的关于t的一维傅里叶变换，给出f(x,y)的二维傅里叶变换F(u,v)的一个切片，该切片与u轴相交成β角，且通过坐标原点，即F(u,v)=F1(Rfβ(t)).

2滤波反投影算法原理

令u=ρcosβ，v=ρsinβ，则

令x=rcosθ，y=rsinθ，则(1)式可化简为

(2)

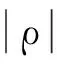
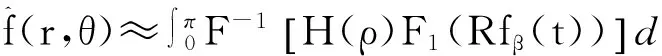
滤波反投影(filterback projection，简称FBP)算法可以通过以下步骤实现[4]：对数据作一维傅里叶变换→用滤波函数H(ρ)进行滤波→对滤波后的数据作傅里叶逆变换→反投影求图像函数.

3常见的滤波函数

第一种：R-L(矩形)滤波函数

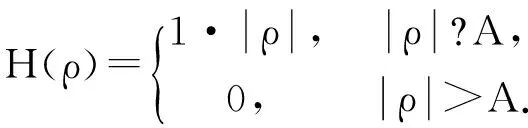
第二种：S-L(shepp-logan)滤波函数

第三种：Hamming 滤波函数

H(ρ)=

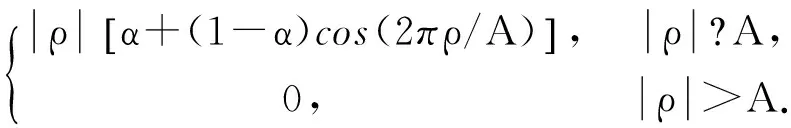
其中α=0.54.

第四种：新滤波函数[5]

其中λ0为归一化常数，ρ为理想滤波函数的频率，A是一个与窗宽有关的正常数.

4重建在计算机上的实现

在仿真试验中，采用经典shepp-logan头部模型进行仿真.重建图像的尺寸512×512.利用等距的扇形束投影重建方法[6]，采用新滤波函数对其进行全局重建. 重建结果如下图所示.

图1　原始图像

图2　新滤波函数重建图像

用其他三种滤波函数进行图像重建的图像，这里不再一一列举. 实验表明采用这四种滤波函数均获得很好的重建图像，用肉眼无法区分.为了客观的对比重建图像效果，笔者计算了重建图像和原始图像的评价值：归一化均方距离(d)、归一化平均绝对距离(r)和最坏情况距离(e)的数值结果.数值结果见表1.

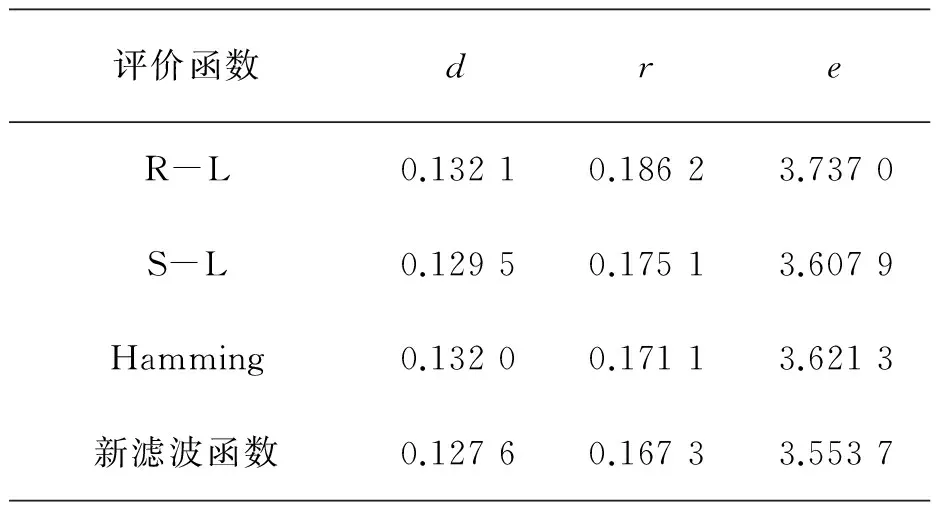
表1　重建结果的图像距离测量值

这三种距离测量值各反映了图像的不同方面：d强调的是少量大误差，r强调的是大量小误差，e强调的是原始图像与重建结果之间的最大密度偏差. 从表1可直观得出：在三个误差计算之中，新滤波函数的值最小，说明新滤波函数整体重建效果较好.

5结论

仿真实验表明，当投影数据较完备时，滤波反投影算法能较好重建出图像，且采用新滤波函数整体评价最好. 而通常情况下，投影数据常常不完备，有时候甚至严重不足，这时候需要采用迭代重建算法. 但无论采用哪种算法，提高重建速度和精度，改善重建图像的质量，仍是今后努力的方向.

参考文献：

[1] 张顺利，李卫斌，唐高峰.滤波反投影重建算法研究[J].咸阳师范学院学报,2008，23(4):47-49.

[2] F. Natterer. The mathematics of computerized tomography[M].Wiley, New York： 1986：9-12.

[3] 庄天戈. CT原理与算法[M].上海：上海交通大学出版社，1992：30-36.

[4] 范惠荣. 关于若干CT图像重建算法的研究[D].内蒙古：内蒙古大学，2003.

[5] 范惠荣，徐茂林，邱钧,等.关于CBP算法的一种新型滤波函数和它的性质[J].电子学报：2004，32(2)：232-235.

[6] 杨艳芳. 基于一种新的扫描方式的滤波反投影算法[D].北京：北京交通大学，2009.

Research on image reconstruction algorithm of filtered back projection

LI Jing

(School of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001，China )

Abstract:CT is one of the application techniques of the image reconstruction, which has been widely used in various fields of natural science. The filtered back projection algorithm is mostly used in image reconstruction at present. On the basis of the theory of image reconstruction, the computer simulation and comparison experiments are carried out on the R-L, S-L, Hamming filter function and the new filter function by the filtered back projection algorithm. The experimental results show that the image quality is better, and the selection of filter function is the key.

Key words:image reconstruction; filtered back projection; filter function; Fourier transform; Radon transform

收稿日期：2015-09-28;修回日期：2015-10-29

基金项目：周口师范学院青年科研基金项目(No.zknuB315209)

作者简介：李静(1986- )，女，河南周口人，助教，硕士，主要研究方向:积分变换与图像处理.

中图分类号：TP391

文献标志码：A

文章编号：1671-9476(2016)02-0074-03

DOI：10.13450/j.cnki.jzknu.2016.02.017