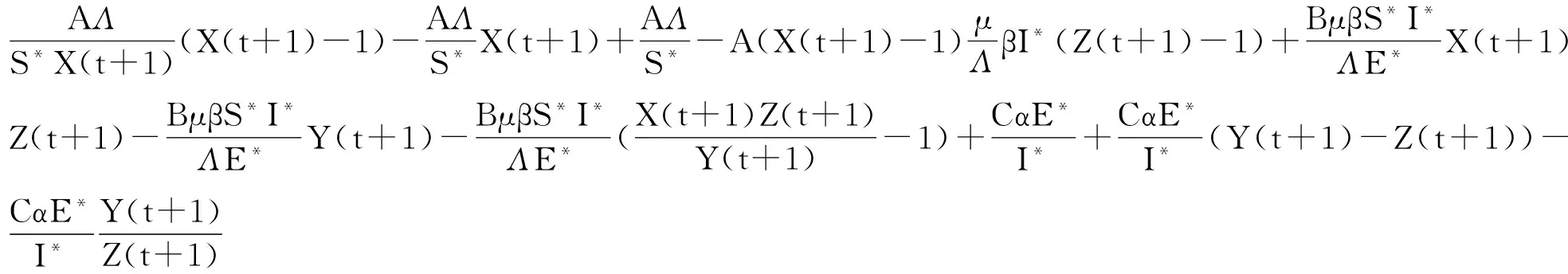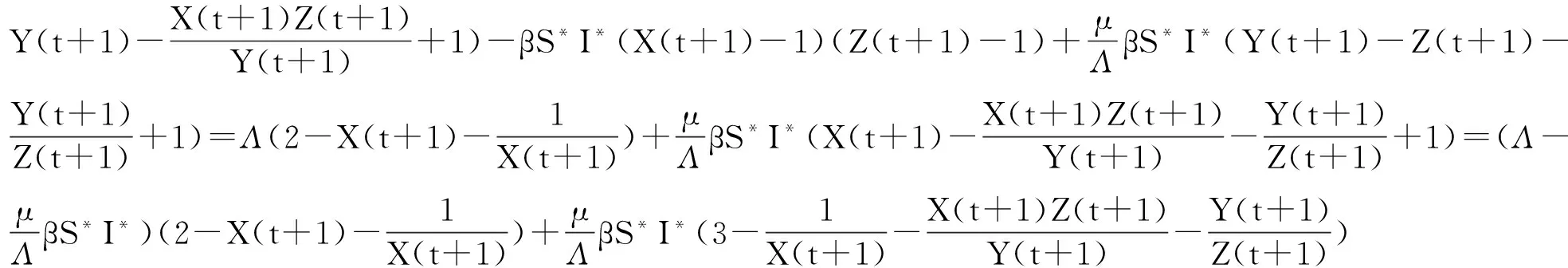具有标准发生率的离散SEIR腮腺炎模型的全局稳定性分析

马　霞 , 陈　娜

(1.太原工业学院 理学系，山西 太原 030008;2.周口师范学院 数学与统计学院，河南 周口 466001)



具有标准发生率的离散SEIR腮腺炎模型的全局稳定性分析

马霞1, 陈娜2

(1.太原工业学院 理学系，山西 太原 030008;2.周口师范学院 数学与统计学院，河南 周口 466001)

摘要：主要研究了一类具有标准发生率的离散SEIR腮腺炎模型的动力学性态.利用再生矩阵的方法定义了模型的基本再生数，通过归纳法得到了模型解的非负性和有界性.当R0<1时，模型存在唯一的无病平衡点并且是全局渐近稳定的.当R0>1时，模型存在无病平衡点和唯一的地方病平衡点，通过构造合理的Lyapunov 函数证明了地方病平衡点是全局渐近稳定的.最后通过数值模拟验证了理论结果.

关键词：离散SEIR传染病模型；向后欧拉法；基本再生数；稳定性；动力学行为

利用数学模型来研究传染病的传播机理和预测传染病的流行趋势已成为共识，应用也越来越广泛.传染病模型与公共卫生、医学、统计学以及计算机仿真等方法的结合使用，能更有效、准确、全面、迅速地给出某地区疾病的流行规律.

由于许多传染病疫情的数据都是按年、月、周、天为单位的离散数据，使得离散模型在参数估计和初值选取以及描述传染病的流行进程等方面更为方便.Allen等[1]研究了离散的SI, SIR, SIS模型.Castillo-Chavez[2]和Yakubu[3]研究了离散SIS模型的复杂动力学性态.Y. Zhou等[4-6]研究了具有年龄结构的离散SIS模型的动力学行为.现在越来越多的人对离散传染病模型的研究感兴趣，离散传染病模型的应用和研究也越来越多.

流行性腮腺炎是由腮腺炎病毒引起的儿童和青少年中常见的呼吸道传染病.主要通过呼吸道分泌液飞沫经空气传播.腮腺炎病毒在腮腺炎肿胀之前数天就潜伏于唾液中，感染者在感染初期不会患病，感染者在康复后即获得永久免疫力.因此，可以利用SEIR模型来研究腮腺炎的传播流行特征.Guo,Moghadas等[7-8]人建立了腮腺炎传染病模型，得出模型的基本再生数，通过构造恰当的Lyapunov函数,研究了模型的全局动力学性态.关于连续SEIR模型的研究有很多，然而，由于理论方法的限制，对于离散SEIR模型的地方病平衡点的全局渐近稳定性的结果很少.本文通过构造合适的Lynapunov函数得到了具有标准发生率的离散SEIR腮腺炎模型的地方病平衡点的全局渐近稳定性.

本文在一定合理的假设下，利用隐式欧拉法建立离散SEIR腮腺炎模型，对该模型解的渐近性态进行比较全面的分析.最后，通过数值模拟验证理论结果.

1 离散SEIR腮腺炎模型

(1)

把模型(1)中的方程相加可得

利用极限系统理论可得模型(1)的极限系统如下：

(2)

下面主要研究系统 (2), 极限系统理论可以保证系统 (2) 与系统 (1) 有相同的动力学性态.

引理1模型(1)关于初始条件(S(0),E(0),I(0),R(0))∈Ω的解(S(t),E(t),I(t),R(t))都是正的.

证由模型(1)可解得

因此

通过计算可得

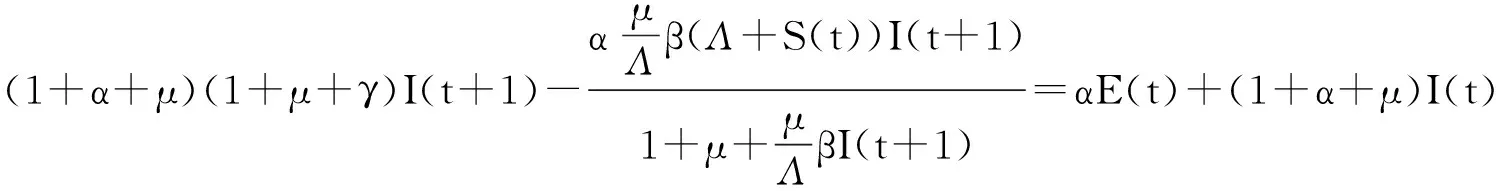
整理后可得如下二次方程

a0I2(t+1)+a1I(t+1)+a2=0.

其中，a0=β(1+α+μ)(1+μ+γ),a2=-(1+μ)[αE(t)+(1+α+μ)I(t)],

当t=0时，由初始条件(S(0),E(0),I(0),R(0))∈Ω可知，常数项a2<0，又知a0>0，因此，上述二次方程

a0I2(t+1)+a1I(t+1)+a2=0.

有唯一的正根I(1)>0，由模型的第一、三、四个方程可得S(1)>0,E(1)>0和R(1)>0.采用类似于上述的方法，可以得到S(2)>0,E(2)>0,I(2)>0和R(2)>0, 最后用数学归纳法可得，对一切t∈Ζ+,都有S(t)>0,E(t)>0,I(t)>0和R(t)>0.

2无病平衡点的存在性和全局稳定性

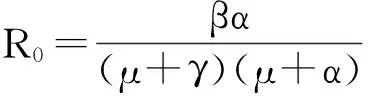
定理1如果R0<1,模型(2)的无病平衡点P0在Ω内是全局渐近稳定的；如果R0>1，则P0是不稳定的，且除了S轴以外，从Ω内充分靠近点P0出发的解都远离P0.

证假设Lyapunov函数V(t)=αE(t)+(α+μ)I(t)，则

ΔV=V(t+1)-V(t)=αE(t+1)+(α+μ)I(t+1)-αE(t)-(α+μ)I(t)

[αβ-(α+μ)(μ+γ)]I(t+1)=(α+μ)(μ+γ)I(t+1)(R0-1)0.

3 地方病平衡点的存在性和全局稳定性

令P*(S*,E*,I*,R*)是模型的地方病平衡点，则S*,E*,I*,R*满足下面的方程

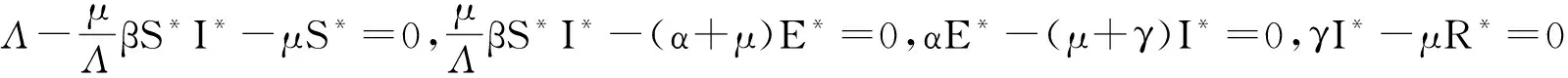
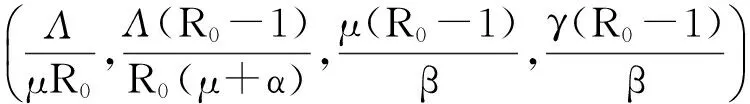
定理2当R0>1时，模型 (2) 的地方病平衡点P*(S*,E*,I*,R*)是全局渐近稳定的.

构造Lyapunov函数V1(t)=Ag(X(t))+Bg(Y(t))+Cg(Z(t))，其中,g(x)=x-1-lnx.由于当x>0时，lnx

同理可得

由方程(3)可得

令

可得

图1　R0=0.654<1，P0的全局渐近性态

4 数值模拟

通过数值模拟来验证分析理论结果，选取参数值Λ=30,μ=0.006,α=0.01,γ=0.08, 当β=0.09时，基本再生数R0=0.654<1. 选取不同的初始值来做数值模拟，数值模拟的结果显示模型的解最终趋于无病平衡点P0(5 000,0,0,0)(如图1)，即R0<1时，无病平衡点是全局渐近稳定的，疾病将会消除.固定其他参数值，变动β的值，当β=0.29时，R0=2.108>1，数值模拟的结果显示模型的解最终趋于地方病平衡点P*(2 372,985,115,1 527) (如图2)，即R0>1时，地方病平衡点P*是全局渐近稳定的.

图2　R0=2.107>1，P*的全局渐近性态

5 结论

本文主要研究了一类具有标准发生率的离散SEIR腮腺炎模型的的动力学性态，得到了模型的基本再生数，模型解的有界性和非负性，分析了模型的动力学性态，结果表明当R0<1时，模型存在唯一的无病平衡点并且是全局渐近稳定的，当R0>1时，模型还存在唯一的地方病平衡点并且是全局渐近稳定的.数值模拟的结果验证了理论结果的正确性.

参考文献：

[1]Allen L. Some discrete-time SI, SIR, and SIS epidemic models[J]. Math. Biosci.,1994, 124: 83-105.

[2]Castillo-Chavez C, Yakubu A. Discrete-time SIS models with complex dynamics[J]. Nonliear Analysis: Theory, Methods and Applications, 2001, 47: 4753-4762.

[3]Franke J, Yakubu A. Discrete-time SIS epidemic model in a seasonal environment[J]. SIAM J. Appl. Math., 2006, 66: 1563-1587.

[4]Zhou Y C, Paolo F. Dynamics of a discrete age-structured SIS models[J]. Discrete and Continuous dynamical systems, series B. 2004, 4: 843-852.

[5]Cao H, Zhou Y C. The discrete age-structured SEIT model with application to tuberculosis transmission in China[J]. Math.Comput. Model., 2012, 55(3):385-395.

[6]Zhou Y C, Ma Z E. Global stability of a class of discrete age-structured SIS models with immigration[J]. Math. Biosci. Eng., 2009, 6:409-425.

[7]Hongbin Guo, Michael Y Li, Zhisheng Shuai. A graph-theoretic approach to the method of global lyapunov functions[J]. Proceedings of the American Mathematical Society, 2008,136: 2793-2802.

[8]S M Moghadas, A B Gumel. A mathematical study of a model for childhood diseases with non-permanent immunity[J]. Comput Appl Math, 2003,157:347-363.

[9]Diekmann O, Heesterbeek J, Metz J. On the definition and the computation of the basic reproduction ratio R0in models for infectious diseases[J]. J. Math. Biol., 1990, 35: 503-522.

[10]Allen L, van den Driessche P. The basic reproduction number in some discrete-time epidemic models[J]. J. Difference Equations and Applications., 2008,14: 1127-1147.

[11]Elaydy S. An introduction to difference equations[M]. New York: Sprink, 2004.

The global stability of a discrete SEIR epidemic model of mumps with standard incidence

MA Xia1,CHEN Na2

(1.Science Department,Taiyuan Institute of Technology,Taiyuan 030008;2.Dept. of Math., Zhoukou Normal University, Zhoukou 466001,China)

Abstract:The dynamical behavior of discrete SEIR epidemic model with standard incidence is studied. The basic reproductive number of the model is defined by using the regeneration matrix. The nonnegativity and boundless of solutions are analyzed by inductive method. It is proved that the disease-free equilibrium is globally asymptotically stable if R0<1, and the endemic equilibrium is globally asymptotically stable if R0>1by constructing reasonable Lyapunov function. Numerical simulations are done to show our theoretical results.

Key words:discrete SEIR model; backward euler method; basic reproductive number; globally asymptotically stability; Lyapunov function

收稿日期：2015-12-12;修回日期：2016-01-07

基金项目：周口师范学院青年科研基金项目(No. zknuB315202);太原工业学院青年科研基金项目(No. 2015LQ19)

作者简介：马霞(1990- )，女，硕士，助教，研究方向：生物数学、动力系统.

中图分类号：O175

文献标志码：A

文章编号：1671-9476(2016)02-0039-05

DOI：10.13450/j.cnki.jzknu.2016.02.008