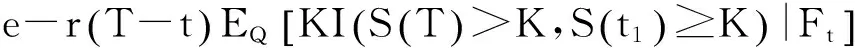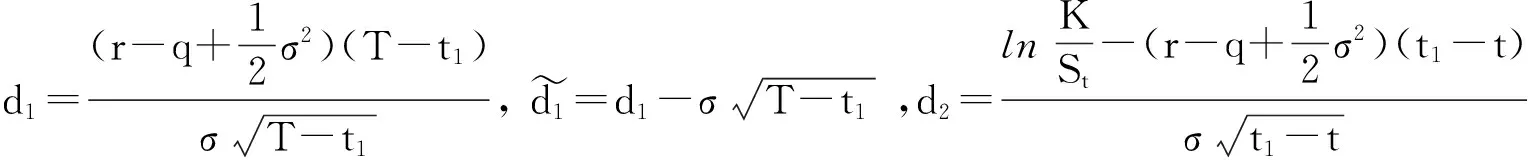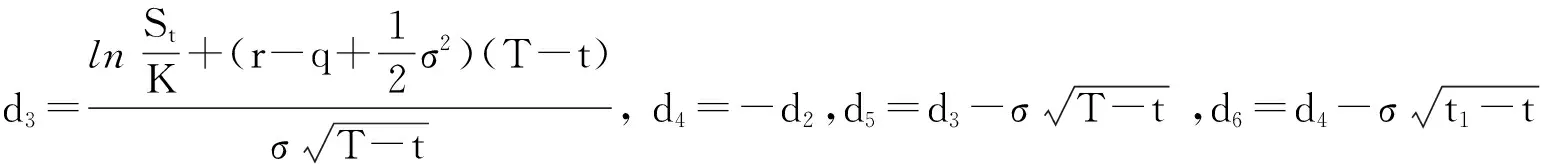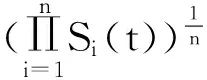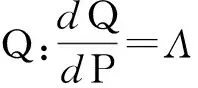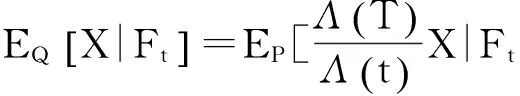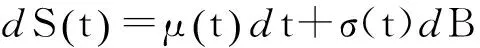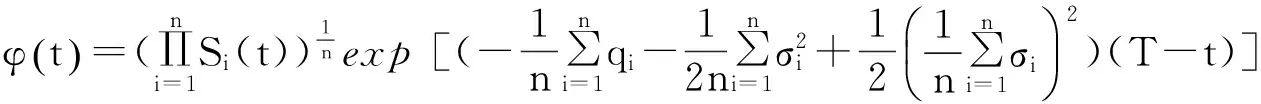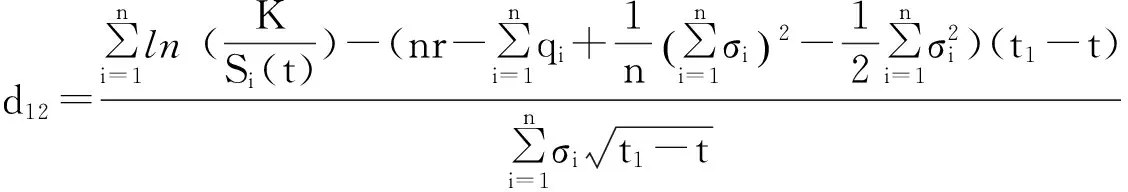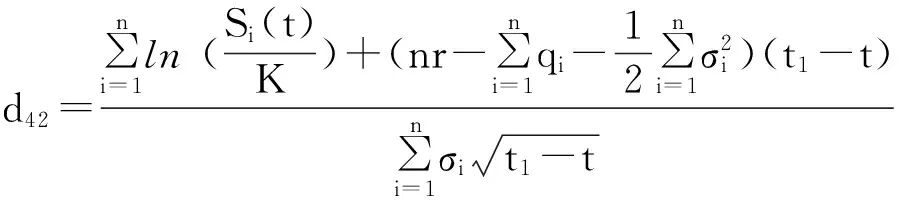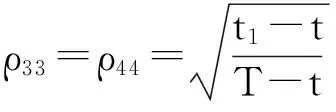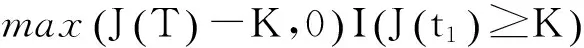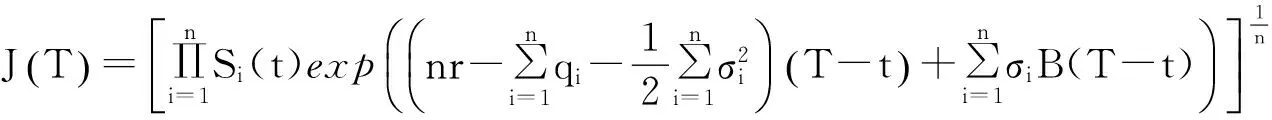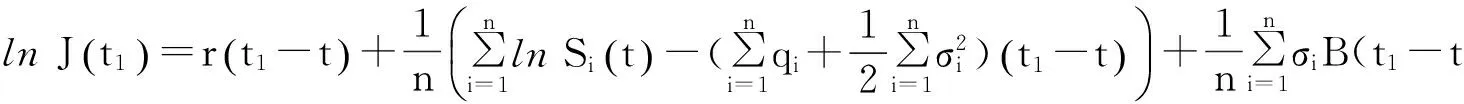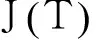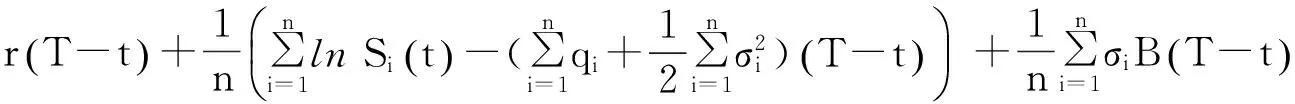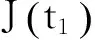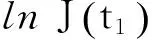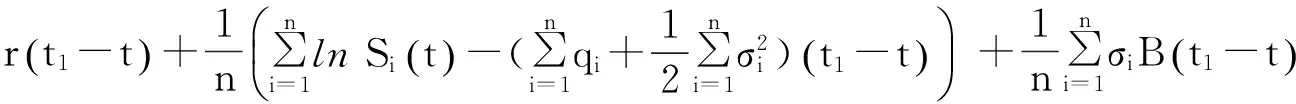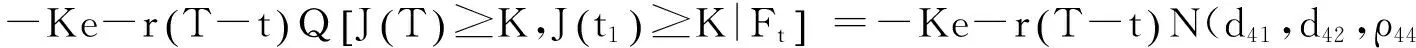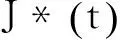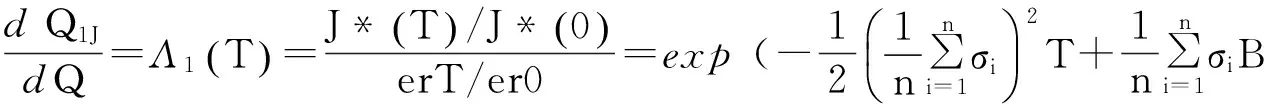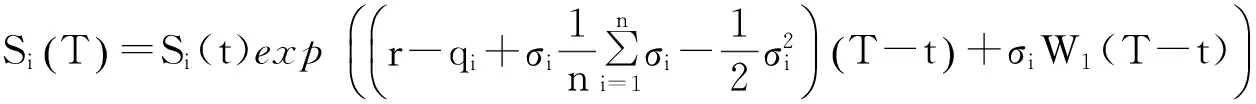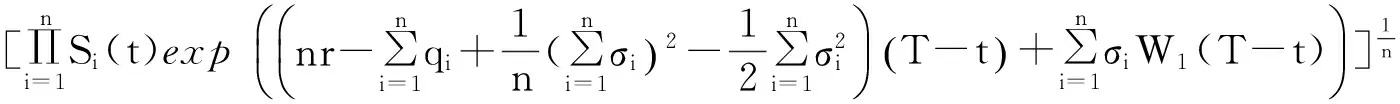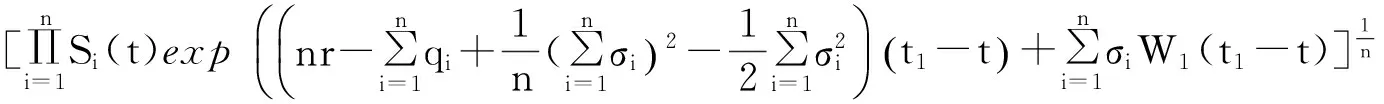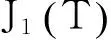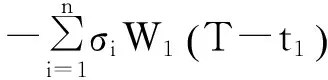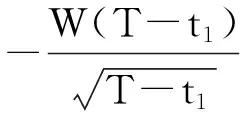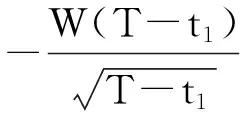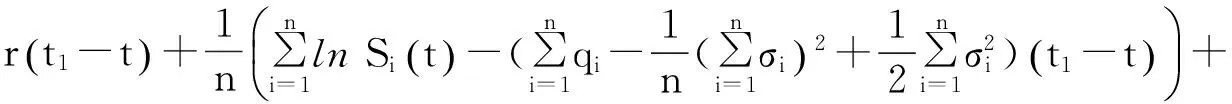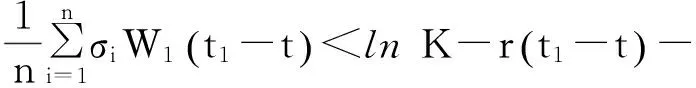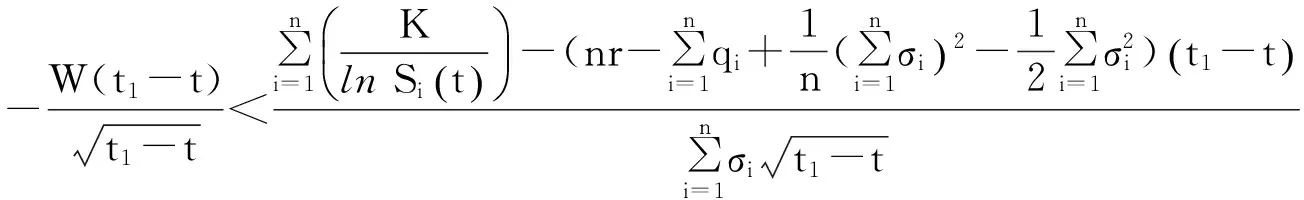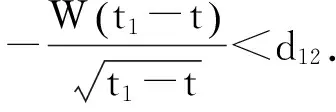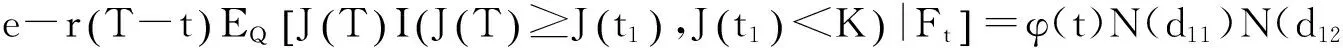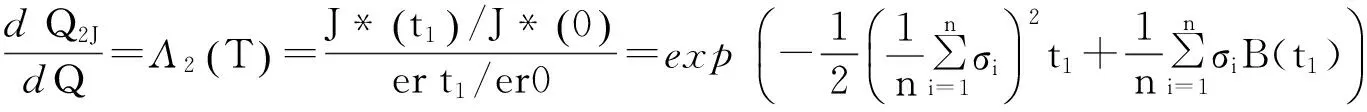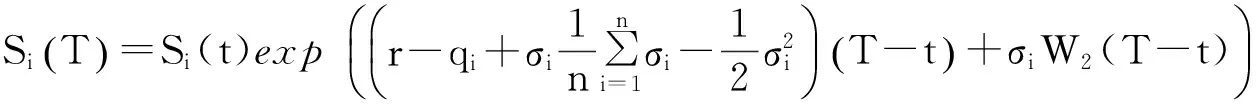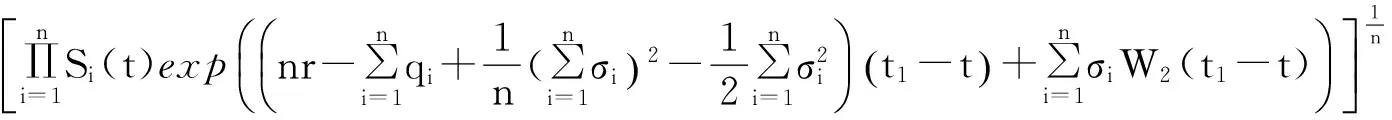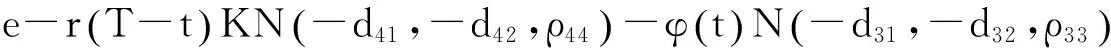基于多个资产几何平均值的重置期权的定价

石　伟,刘丽霞

(河北师范大学 数学与信息科学学院, 河北 石家庄 050024)



基于多个资产几何平均值的重置期权的定价

石伟,刘丽霞

(河北师范大学 数学与信息科学学院, 河北 石家庄 050024)

摘要：标准的重置期权都是针对单一资产而设定的, 这样的重置期权容易被操控. 为了避免这种情况, 对标准重置期权进行改良, 定义了一种基于多个资产几何平均值的新型重置期权. 在风险中性测度下, 利用等价鞅测度变换和Girsanov定理得到了带常数股息的股票上的此种新型重置期权精确的定价公式, 推广了以前已有的结果.

关键词：重置期权;测度变换;Girsanov定理

自金融衍生工具出现以来, 衍生业务发展日益蓬勃, 越来越多的人希望借助它们来帮助自己规避风险, 获得收益. 期权[1], 作为一种十分流行的金融衍生工具, 近几十年来, 国内外诸多学者对其定价问题开展了大量的研究工作, 并获得了许多具有实际意义的研究成果. 众所周知, 最基本的期权为欧式看涨/看跌期权, 美式看涨/看跌期权. 以欧式看涨期权为例, 它给予持有者在将来的某一时刻以某一固定价格买入一资产的权利. 使得投资者在T时刻获得的收益为

max(S(T)-K).

随着投资者的需要, 市场上逐渐出现了多种多样的奇异期权, 如障碍期权[2]、回望期权[3]、重置期权[4-8]等等. 重置期权是一种应用十分广泛的奇异期权, 它给予投资者在某个或某几个预设日期将期权合约中的执行价格重新设置成预设日期时标的资产价格的权利. 以标准重置看涨期权为例, 它使得投资者在T时刻的收益为

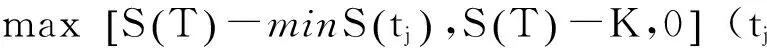
根据定义可知, 与一般的欧式看涨期权相比, 它给投资者带来更多的收益机会. 到目前为止, 针对重置期权已经有了大量的研究成果: 刘邵容研究了O-U过程模型下一种回望型重置期权, 并得到了这种回望型重置期权的精确定价公式[4]; 李淑锦研究得到了随机利率模型下重置期权的定价公式[5]; Stephen及Robert研究了重置看跌期权的定价问题, 并得到了精确的定价公式[6]. 还有许多研究结果[7-8], 这里不一一列举.

以上这些已有的结果都是针对单一资产的重置期权进行研究所得到的, 通过对重置期权的进一步分析可知, 这种单一资产的重置期权有它自身的缺陷. 由于期权中的标的资产是单一的, 所以它的价格易被投资者所控制, 使其趋于对自身有利的方面, 从而导致了市场上不公平交易的结果, 造成不良的市场氛围. 所以现将重置期权进行一定的改良创新, 构造一种新型的重置期权, 它将标准重置期权中的标的资产替换为市场上多个资产的几何平均值, 这样可以防止投资者对预设日期资产价格和到期日资产价格两方面的操控. 设其在有效期内只有一个预设日期, 这样就避免了因投机者对资产价格控制而造成的不公平交易.

本文在介绍奇异期权研究现状的基础上,给出了标准重置期权的定义及定价公式, 建立了新型重置期权的定义及精确的定价公式.

1 标准重置期权的定价公式

考虑不确定性由概率空间(Ω,Ft,Q)(其中Q是风险中性测度, Ft是t时刻的信息流)表示重置期权的价格.

标准重置期权的定义[7]:现有一个资产S(t), 设其为期权中的标的资产. 设期权的预设日期为t1, 在预设日期t1, 期权持有者有将执行价格K重置为这个资产当前价格S(t1)的权利.

假设标的资产价格S(t)在风险中性测度Q下服从几何布朗运动

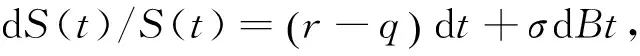
(1)

其中q,σ为常数, 利率r也为常数.

示性函数I(S(t1)

根据标准重置期权的定义, 可以得出标准重置看涨期权持有者在T时刻获得的收益:

当t≥t1时,I(S(t1)

其中BS(t,S,K,T)是执行价格为K, 到期日为T的欧式看涨期权用BS模型所求得的价格[9].

当t< t1时, 重置期权在t时刻的价格为

(2)

定理1[7]标准重置看涨期权t时刻的定价公式为

(3)

其中

2基于多个资产几何平均值的重置期权的定价

研究一种新型重置期权并得到其精确的定价公式.

这里只考虑t

假设资产价格Si(t)在风险中性测度Q下服从几何布朗运动

(4)

因为这些股票是在同一个市场环境下的股票, 所以假设它们所服从的过程中的布朗运动是一样的.

引理2[10]令S(t)满足以下随机微分方程：

如果f(x)是一个二次连续可微函数, 则过程Y(t)=f(S(t))的随机微分方程存在且为:

定理2由定义1所定义的新型重置期权的定价公式为:

(5)

其中

证期权在t时刻的价格为

整理得到

(6)

对式(4)应用伊藤公式, 求得

(7)

则这n个资产在t1和T时刻的几何平均值为

基于出行连续性识别公交刷卡乘客下车站点模型是建立在日刷卡次数在2次及以上的基础上，根据公交乘客出行具有连续性规律，即公交乘客往往会在上次出行的目的地乘车返回上次出行的出发地. 采用该模型对IC卡乘客的出行OD进行识别，仅有一次IC卡刷卡记录和所有IC卡1 d内的最后1次刷卡记录不在本算法考虑范围内. 具体步骤为：

(8)

(9)

应用式(8)～(9)的结果, 由布朗运动的独立增量性质可以直接计算公式(6)中的第四项

所以,得到式(6)中的第四项:

(10)

为了能够应用Girsanov定理, 设QJ是以

(11)

则可得到Q1J测度下股票价格和股票价格t1时刻几何平均值的表达式分别为:

(12)

(13)

(14)

应用式(13)～(14)及布朗运动的独立增量性质, 公式(6)中的第一项:

所以,得到式(6)中的第一项:

(15)

定义新测度如下:

(16)

则可得到Q2J测度下股票价格和股票价格t1时刻几何平均值的表达式分别为:

(17)

(18)

应用式(17)～(18)及布朗运动的独立增量性质, 公式(6)中的第二项:

(19)

其中ψ(t)为式(5)中的表达式.

类似于第一项的求法, 应用式(7)～(8)的结果, 公式(6)中的第三项:

综上所述, 证明了新型期权的定价公式即为式(6).

定理3设资产价格Si(t)满足以上假设的所有条件, 则新型重置看跌期权的价格为:

(20)

其中Φ(t),Ψ(t),d11,d12,d21,d22,d31,d32,ρ33,d41,d42,ρ44与前文式(6)中的结果一样.

注:当Si(t)与S1(t)的分布都相同时, 所得的结果即为第二部分中定理1中的结果(3).从而，本文的结果为文献[7]中定理的推广.

参考文献：

[1]Black F, Scholes M. The Pricing of Option and Corporate Liabilities[J]. Journal of Political Econ-omy, 1973, 81(3): 637-659.

[2]张斌. 障碍期权的定价及其应用[D]. 南京: 南京理工大学, 2004.

[3]王利伟. 回望期权定价模型的研究[D]. 北京: 北方工业大学, 2008.

[4]刘邵容, 杨向群. O-U过程模型下一种回望型重置期权的定价[J]. 湖南师范大学自然科学学报, 2007,30(4):23-26.

[5]李淑锦,李胜宏. 随机利率下奇异期权的定价公式[J].数学学报(中文版),2008,5(2):299-310.

[6]Stephen F Gray, Robert E Whaley. Reset Put Options: Valuation, Risk Characteristics, and an Application [J]. Australian Journal of Management, 1999, 24(1):1-20.

[7]李松芹. 重置期权定价问题的研究[D].上海: 上海师范大学, 2006.

[8]Massimo Costabile, Ivar Massabó. On pricing arithmetic average reset options with multiple reset dates in a lattice framework [J]. Journal of Computational and Applied Mathematics, 2011,235:5307-5325.

[9]Yue-Quen Kwok. Mathematical Models of Financial Derivatives Second Edition [M]. Springer, 2010 .

[10]Klebaner F C. Introduction To Stochastic Calculus With Applications[M]. 北京: 人们邮电出版社, 2008.

The pricing of the reset option based on the geometric average of multiple assets

SHI Wei, LIU Lixia

(College of Mathematics and Information Science, Hebei Normal University,Shijiazhuang 050024,China)

Abstract:The standard reset option is about one asset, it can be controlled easily. Now we define a new reset option, which is based on the geometric average of multiple assets. By Girsanov theorem and the theory of equivalent martingale, we give the exact pricing formulas of this new option on the assets with constant dividend yield under the risk neutral measure, thus we extend the result before.

Key words:reset option; change of measure; Girsanov theorem

收稿日期：2015-03-20;修回日期：2015-09-24

基金项目：国家自然科学基金(No.11501164)

作者简介：石伟(1990- ),女,河北秦皇岛人，硕士研究生，研究方向:金融工程与风险管理.

中图分类号：O211.6

文献标志码：A

文章编号：1671-9476(2016)02-0004-07

DOI：10.13450/j.cnki.jzknu.2016.02.002