薄板结构低噪声仿生拓扑优化方法

滕晓艳　江旭东　史冬岩

1.哈尔滨工程大学，哈尔滨，150001　　2.哈尔滨理工大学，哈尔滨，150084



薄板结构低噪声仿生拓扑优化方法

滕晓艳1江旭东2史冬岩1

1.哈尔滨工程大学，哈尔滨，1500012.哈尔滨理工大学，哈尔滨，150084

摘要：针对薄板结构的低噪声设计问题，以结构声辐射功率最小化为优化目标，借鉴植物脉序分枝结构的构型特征，提出了薄板结构加强筋布局的仿生拓扑优化方法。以结构应变能最小和释放局部最大剪应力作为加强筋主脉和次脉的生长准则，以广义Murray准则作为加强筋脉序的分歧准则，构造了具有脉序分级特征的加强筋自适应生长算法。以固支薄板结构的横向弯曲振动及声辐射问题为典型算例，对比分析了仿脉序分布加筋板结构的声辐射功率和振动功率流的分布特性。数值结果表明，与相同体积约束下的正交加筋布局方式相比，仿脉序分布加筋方法使薄板结构具有更优的声振特性，进而验证了薄板结构加强筋仿生布局降噪方法的有效性与可靠性。

关键词：仿生设计；加强筋布局；拓扑优化；薄板结构；低噪声

0引言

加筋板壳结构具有质量小、强度高、刚度大等优点而被广泛应用于船舶与海洋结构中。舰船薄壁结构中加强筋的布局方式与结构的声振耦合特性密切相关，相应的吸振抑波能力将直接影响舰船的声隐身性能。因此，通过结构优化方法，对振动声源结构设计区域的材料、阻尼和刚度进行合理布局，对减小舰船水下辐射噪声、增强舰船生命力无疑具有非常积极的作用。

在舰船实际结构中，加强筋分布形式多呈现平行、井字、米字或它们的简单组合，研究工作主要通过优化加强筋形状参数和分布间距来减小结构的机械振动噪声[1-4]。上述方法尽管改善了结构的声振耦合性能，但是传统的加强筋分布方式未沿结构的最优传力路径布局，加强筋的分布构型并不是最优的。为了克服上述缺点，杜建镔等[5-6]、史冬岩等[7]利用连续拓扑优化方法，通过优化材料在结构设计域内的拓扑分布来使谐振结构辐射声场中的声压或声功率最小化。由于连续拓扑优化方法将加强筋的设计问题转化为结构的厚度分布设计问题，故无法直接获得加强筋清晰的几何轮廓与分布形态。

近年来，基于植物分枝结构的最优性及其成长原理[8-9]提出的结构仿生设计方法在板壳结构件加强筋布局优化方面已经取得初步进展[10-16]。丁晓红等[10-11]通过研究植物根系形态形成机理，针对薄板结构的静刚度与频率优化问题，提出了薄板结构的加强筋自适应生长设计方法。Ji等[12]针对启发式寻优算法的缺陷，采用准则法结合数学规划法求解板壳结构加强筋布局优化问题，提出了基于卡罗需-库恩-塔克最优准则的板壳结构加筋自适应成长方法。文献[13-16]借鉴叶脉结构特征与分枝系统分布形态的最优性原理，针对薄板结构的静态强度和刚度优化问题，提出了基于叶脉分枝结构的薄板结构加强筋布局仿生设计方法。现有的结构仿生拓扑优化方法局限于板壳结构的静态强度、刚度和动力特性的优化问题，针对加强筋构型和分布形态的声学优化设计方面的研究相对较少。

本文通过分析植物脉序不同结构层次(主脉和次脉)的功能结构、几何构型和形态特征等规律及其原理，提取叶脉生长和分歧的力学准则。以结构声辐射功率最小化为优化目标，基于板梁理论建立加强筋主脉和次脉生长的灵敏度公式，利用脉序分歧准则修正局部脉序的截面尺寸，构造具有脉序分级特征的加强筋自适应生长算法。通过典型薄板结构加强筋分布的声学优化设计，对比分析原型薄板结构、正交加筋板结构和仿生优化结构的声辐射功率和振动功率流特性，验证加强筋仿生布局优化算法的可行性和有效性。

1板梁耦合结构的声振理论模型

基于经典薄板和梁振动理论，建立加筋板声辐射的板梁声振理论模型。根据结构声强理论，建立加筋板的振动功率流模型，从能量的角度分析板梁耦合结构振动能量的分布和传播途径。

1.1板梁耦合结构的简谐振动

假设加强筋和薄板之间是刚性连接，在每个加强筋和薄板的线接触处，加强筋和薄板具有在z方向上相同的位移和关于x、y轴的相同转角(图1)。单层加筋板的一侧充满流体介质(假设为空气)，另一侧受到简谐激振点力F0ejωt的作用。基于Kirchhoff薄板理论，薄板单元的运动方程为

bp4wp+ρh=[F0δ(x-l)δ(y)+

(1)

4=(∂2/∂x2+∂2/∂y2)2

式中，wp为薄板的横向位移；bp、ρ、h分别为薄板的弯曲刚度、密度和板厚；Fp(y)、Mpy分别为加强筋作用于板上单位长度的法向力和扭矩激励；δ(·)函数表示作用力的位置与分布；ω为激振频率。

图1　简谐力作用下的板梁耦合结构模型

基于Eluer-Bernouli梁理论，加强筋单元的运动方程为

(2)

(3)

式中，wb为加强筋的横向位移；Fb(y)、Mby(y)分别为薄板作用于加强筋的反力和反力矩，满足Fb(y)=-Fp(y)和Mby(y)=-Mpy(y)；ρ′、E、G分别为加强筋材料的密度、弹性模量和剪切模量； I、J分别为加强筋轴截面关于中性轴的惯性矩和关于截面中心的极惯性矩；A、I0分别为加强筋轴截面面积和转动惯量。

1.2板梁耦合结构的振动功率流

对应于空气噪声的声强法可以用来诊断结构缺陷、识别结构噪声源、确定结构噪声源的大小和判断结构噪声的主要传播途径，它是解决结构振动和噪声问题的一种有效手段。结构声强可以看作是功率流密度，对于薄板结构，结构声强可以分解为沿x、y两坐标轴方向上的分量，它们满足如下关系：

(4)

(5)

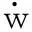
对于一维梁而言，wb与坐标x无关，将式(4)、式(5)简化，则加强筋的结构声强表示为

(6)

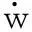
1.3板梁耦合结构的声辐射模型

在结构-声辐射计算中，假设薄板结构镶嵌于无限大障板上，加强筋只对结构振动有影响。忽略辐射声场在流体传播中的损失，不计结构对声能量的吸收，因而辐射声场中的声能量与结构表面的声辐射能量相等。

对于板梁耦合结构，单频激振时振动表面的声强Is和声辐射功率W分别为

(7)

(8)

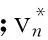
由板梁振动控制方程式(1)～式(3)，通过有限元法求解上述板的控制方程得到加筋板结构的振动响应。根据板梁结构声强方程式(4)～式(6)，分析加筋板结构的振动功率流特性；由板梁耦合结构-声辐射方程式(7)、式(8)，计算加筋板结构辐射声场的声强与声辐射功率。

2加强筋仿叶脉布局优化算法

暴露在空气中的叶片长期承受的机械载荷多为自然风激励和雨水冲击等动载荷，它在自然载荷的塑造作用下，经过长期的自然选择，具有抵抗静载荷作用的静力学性能和承受动载荷激励的动力学性能。若将叶片视为工程上的板壳结构，则叶脉可被视为其上分布的加强筋。叶脉是叶片刚度和强度的主要贡献者，因此本文通过分析植物脉序的几何构型、分布形态和谐振性能的力学关系，建立加强筋脉序生长的力学准则，以加筋板结构的声辐射功率为目标，优化加强筋的布局形式，开展薄板结构低噪声仿生拓扑优化方法研究。

2.1优化模型

由于声辐射功率为激振频率的函数，因此将声辐射功率在优化频带内的平均值作为目标函数，则加筋板结构的声辐射优化模型为

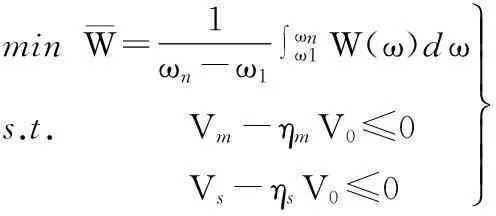
minW=1ωn-ω1∫ωnω1W(ω)dωs.t. Vm-ηmV0≤0 Vs-ηsV0≤0üþýïïïï

(9)

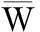
2.2加强筋脉序生长准则

植物分布形态的结构力说[17-18]认为，叶脉的承载能力由三级脉序决定，主脉尺寸最大，承受绝大部分载荷，各级次脉尺寸依次减小，承载能力逐级下降。如果将薄板结构中加强筋的分布构型作为准静态下结构渐进生长的结果，并且生长过程遵循生物进化的最优化准则，那么加强筋生长的“自然选择”过程和植物脉序形态的形成过程具有生物相似性。考虑到单层加筋板的结构特征，根据叶脉分布形态，从原型薄板结构出发，在材料体积约束下，提取叶脉主脉、一阶次脉结构进行加强筋的低噪声仿生布局设计。

2.2.1基于最小应变能的加强筋主脉生长准则

在叶片内部弹性应力场作用下，主脉的脉序细胞在形成层固定通道中遵循能量损耗最小原则生长，经过自然选择进化为最终的平衡构型[17]。如果将主脉生长过程的能量流理解为结构的弹性变形能，则主脉的几何构型与分布形态具有能量最优性。在简谐激励作用下，加筋板结构的弹性变形能不断转变为辐射声场的声能，因而可将加筋板结构应变能最小化作为加强筋主脉的生长准则。

在单频简谐激励作用下，板壳加强筋结构的速度与位移关系为V=jωu(ω)ej(ωt+φ)，谐振结构的弹性应变能幅值为U(ω)=uT(ω)Ku(ω)/2。因此，谐振结构的弹性应变能与辐射声功率具有正相关关系，则以弹性应变能最小化的主脉生长准则作为加强筋的主体布局准则是合理的。

云南地处中国西南边陲，地理位置十分重要，所以全国编练36镇（师）的计划中，云南占了2个（最后只创建了一个，即1909年建立的19镇）。而讲武堂的创立，就是为了云南编练新军的需要。在四川就得知云南情况的朱德，看准了这个机会，步行70天到了昆明。

在优化频带内，加筋板结构的平均应变能幅值为

(10)

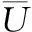
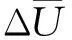
(11)

式中,αi为主脉脉序生长的灵敏度;ΔKi1、Δui1(ω)分别为主脉候选梁单元i生长前后总体刚度矩阵的变化量和结构节点位移列阵的改变量;Ki0为主脉候选梁单元i生长前的总体刚度矩阵。

根据式(11)，计算主脉候选梁单元i生长前后的加筋板结构的平均应变能灵敏度集{αi}，集合中的最小值对应的梁单元节点即为下一段主脉脉序的生长点。

2.2.2基于抑制最大剪应力的加强筋次脉生长准则

植物分布形态的结构力说认为，次脉的生长与剪应力密切相关，尤其是剪应力对脉序分歧处的矢量平衡起着决定性作用[8]。与植物根系的生长过程类似，次脉的生长和分布最大程度地抑制局部最大剪应力以达到剪应力的均匀性[9]。由此，以最大程度地削弱局部最大剪应力作为加强筋次脉的生长准则。

(12)

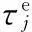
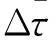
(13)

式中,“∶”为张量并积算子；βi为次脉生长的灵敏度;σ为加筋板结构的柯西应力张量;Δσ为次脉候选梁单元i生长前后柯西应力的改变量。

根据式(13)，计算次脉候选梁单元i生长前后的加筋板结构的最大剪应力均值灵敏度集{βi}，集合中最大剪应力在生长前后得到最大程度削减的次脉待生长点作为下一段次脉的生长点。

2.2.3主脉、次脉种子的选取原则

主脉种子的数量以及位置的选取要遵循“弹性应变能最小准则”。通过选择结构边界或边界附近位置作为主脉种子，在主脉相同体积用量约束下，对比主脉脉序形成后的板梁复合结构的弹性应变能，具有最小弹性应变能的板梁复合结构即为具有最优主脉脉序布局的加筋结构。次脉种子位于主脉上的最大剪应力点，依据抑制最大剪应力的次脉生长准则进行生长，如果遇到基板边界或主脉则终止生长。

2.2.4加强筋脉序分歧的矢量平衡

植物叶脉除宏观上具有等级和闭环结构的特征外，局部脉序分歧处满足基于广义Murray准则的矢量平衡方程[18]。在加强筋脉序重塑阶段，脉络在分歧处微调脉序方向和宽度尺寸，脉序分歧准则遵循如下矢量方程：

(14)

式中,di为分歧处各段脉序的宽度尺寸;ei为脉序横截面的单位外法向矢量;fi为分歧处各段脉序的宽度矢量。

2.2.5加强筋脉序的光滑处理

加强筋脉络生长结束后，得到的最原始的加强筋分布通常都是形状不太规整的粗糙的布局结果。因此，利用最小二乘法拟合脉序分布构型，最终获得加强筋光滑的布局形式。

2.3优化流程

薄板上加强筋的设计过程是一个类似于植物叶脉的“生长进化过程”，加强筋脉序在加筋板的张量场中产生。脉序分为主脉和次脉，主脉在能量场中产生，从初始种子处开始生长，沿着使结构总体应变能最小的方向生长；次脉在应力场中产生，从主脉上最大剪应力处开始生长，沿着局部剪应力削减最大的方向生长。主脉、次脉在分岔处满足矢量平衡方程，最后通过脉序光滑处理得到加强筋仿生构型,如图2所示。

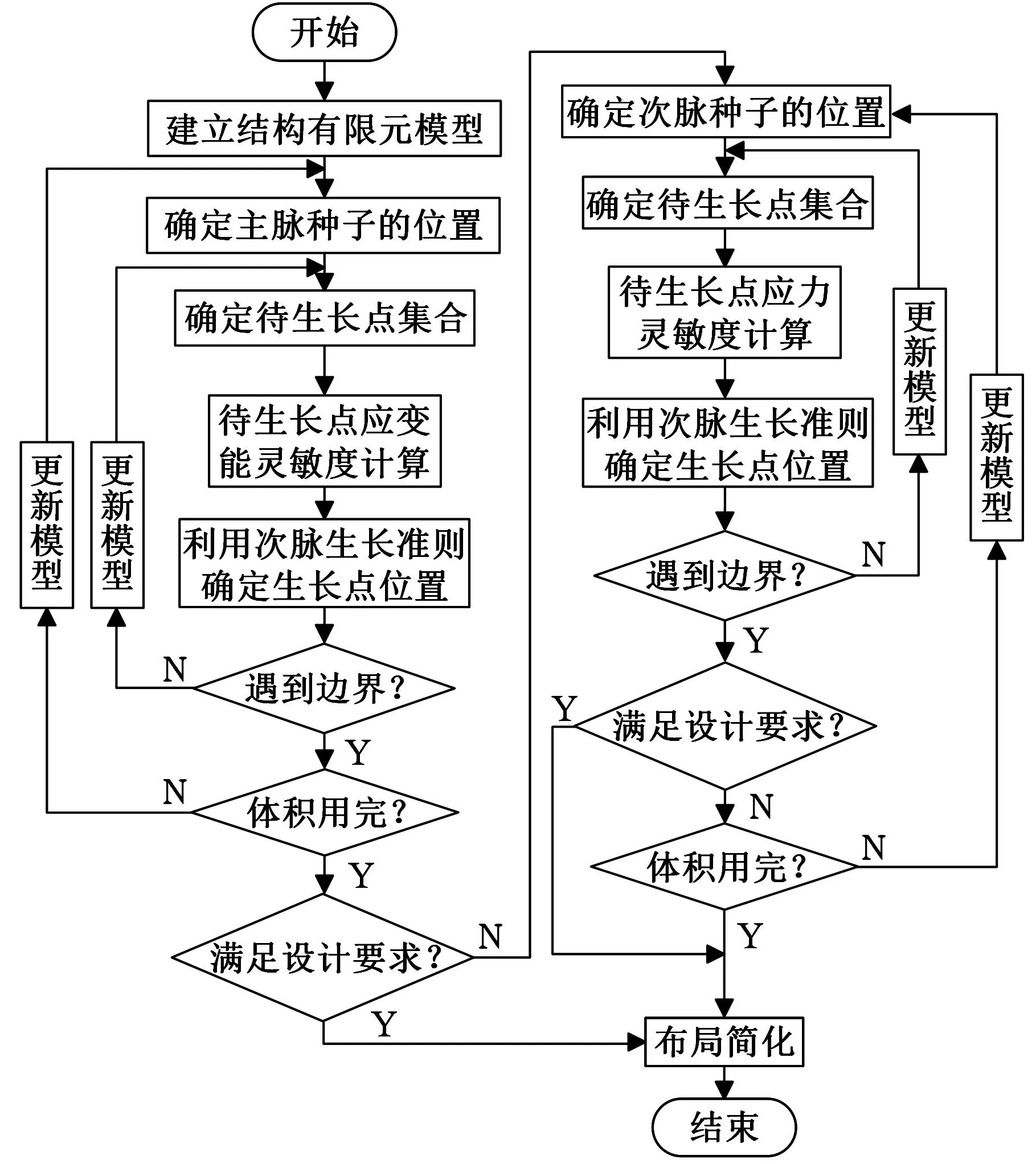
图2　脉序生长算法流程图

3典型算例

3.1对边固支方板

方形薄板对边固支，板的中心处受集中简谐载荷作用(图3a)。方板边长L=0.8 m，厚度为0.01 m，加强筋主脉初始宽度dm0=0.01 m，初始高度hm0=0.016 m，次脉初始宽度ds0=0.005 m，初始高度hs0=0.016 m，主脉体积约束量为0.2V0，次脉体积约束量为0.1V0，简谐激励的幅值Fa=1 N,材料的弹性模量E=210 GPa，泊松比μ=0.3，声速c=342 m/s,，空气密度ρa=1.21 kg/m3，声功率参考值W0=10-12W,优化频段ω为0～1200 Hz。

根据主脉种子选取的“弹性应变能最小准则”，在载荷作用处及两固支边的中点设置主脉种子，载荷处的种子向自由边蔓延生长，形成“十”字交叉形状，固支边上的种子则以“八”字形延伸，最终两股主脉交汇连接；次脉种子位于主脉上靠近薄板四角的位置，向固支与自由边界生长形成辅助支撑。光滑脉络的分布构型，通过矢量平衡准则修正脉序分歧处的截面尺寸，获得加强筋脉序的最终布局形态。与相同体积约束下正交加筋布局方式相比(图3b～图3d)，仿生结构声辐射功率的最大峰值为65.16 dB，低于正交加筋结构的最大峰值72.42 dB；在整个优化频带内，仿生结构声辐射功率的平均值为48.01 dB，也低于正交加筋结构的平均值52.24 dB，因此仿生加筋布局设计能够更有效地降低薄板结构的辐射噪声水平，如图4所示。

(a)对边固支带孔方板　 　 　(b)正交加筋板结构

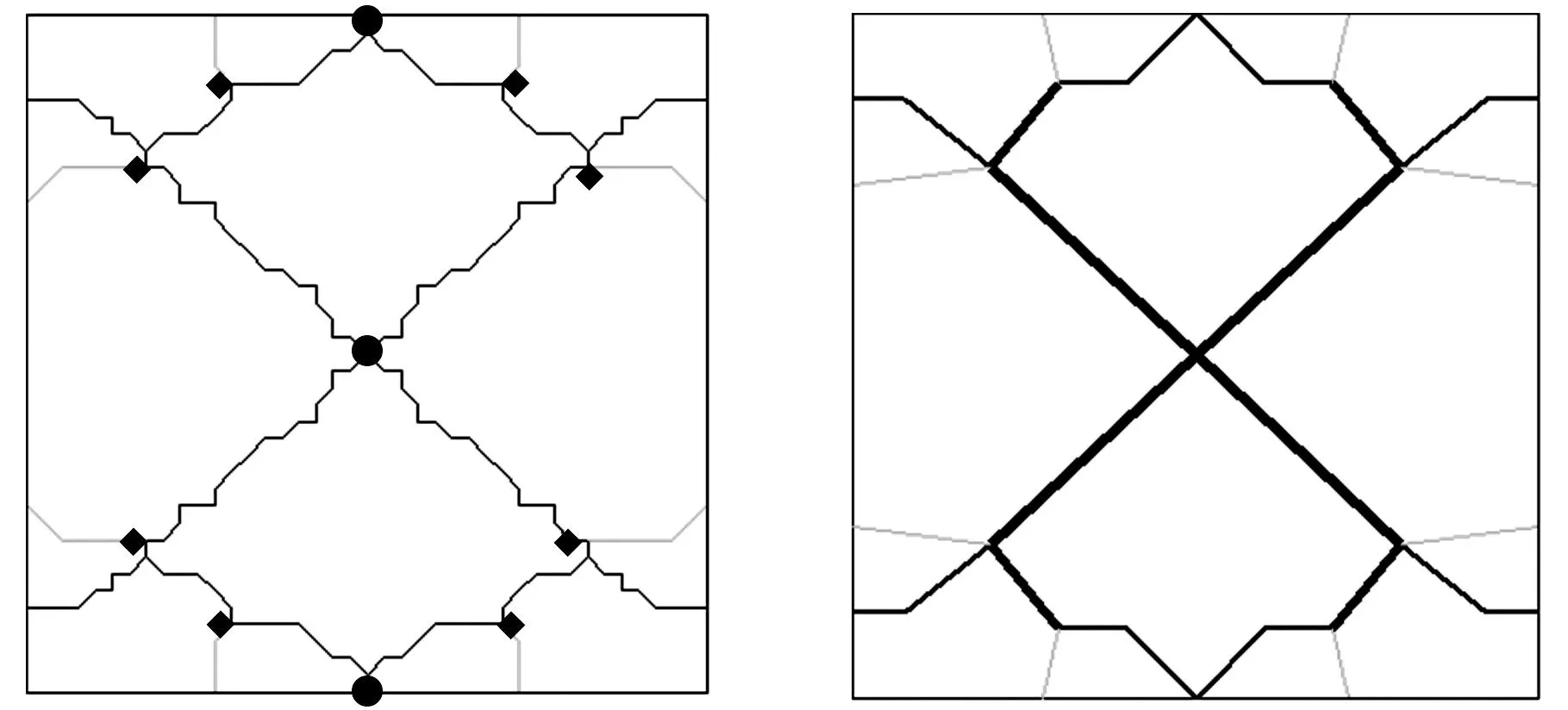
(c)仿脉序加筋计算构型 　 (d)仿脉序加筋光滑构型图3　薄板结构加筋布局方式对比

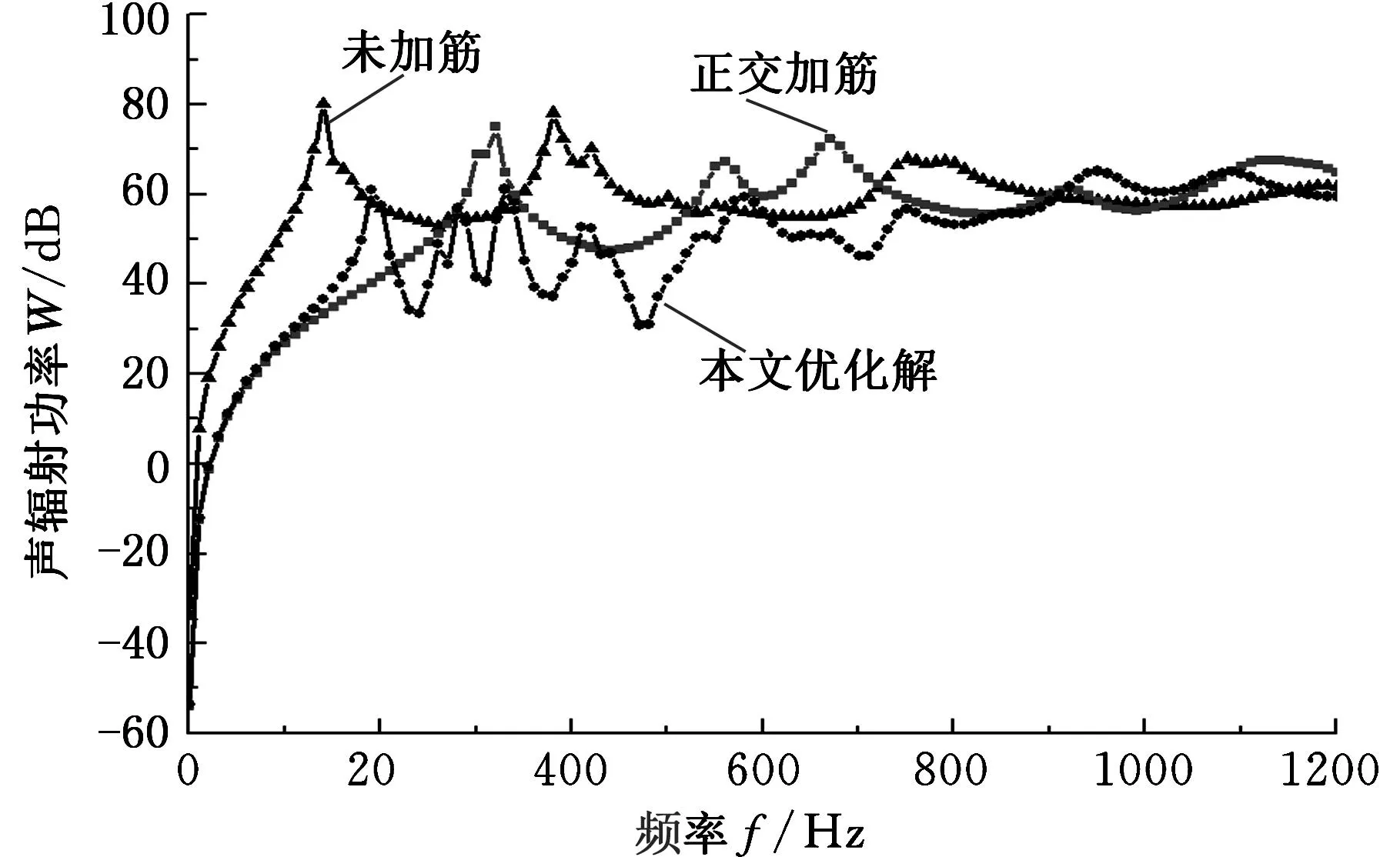
图4　声辐射功率对比

分析仿叶脉布局加筋薄板的振动能量流动特性，对比仿生结构与原型薄板结构的结构声强，揭示仿生结构振动能量的分布和传播机理，如图5所示。原型结构能量主要集中于载荷作用点，同时向四周扩散，由于边界条件为对边固支，能量主要流向自由边，所以在固支边的附近能量分布相对较少。仿生脉序分布加强筋的存在改变了能量的传递路径，促使能量沿着平行于加强筋的方向流动，而只有很小一部分能量能够穿过加强筋进行传递。由于主脉的刚度大，距离激励点近，所以由激励源提供的能量主要向加强筋主脉传递。此外，观察加强筋所形成的封闭区域可以发现，由于加强筋的阻碍，封闭区间内出现了涡流现象，这说明该区域内能量的流入与流出相等，振动能量是守恒的。

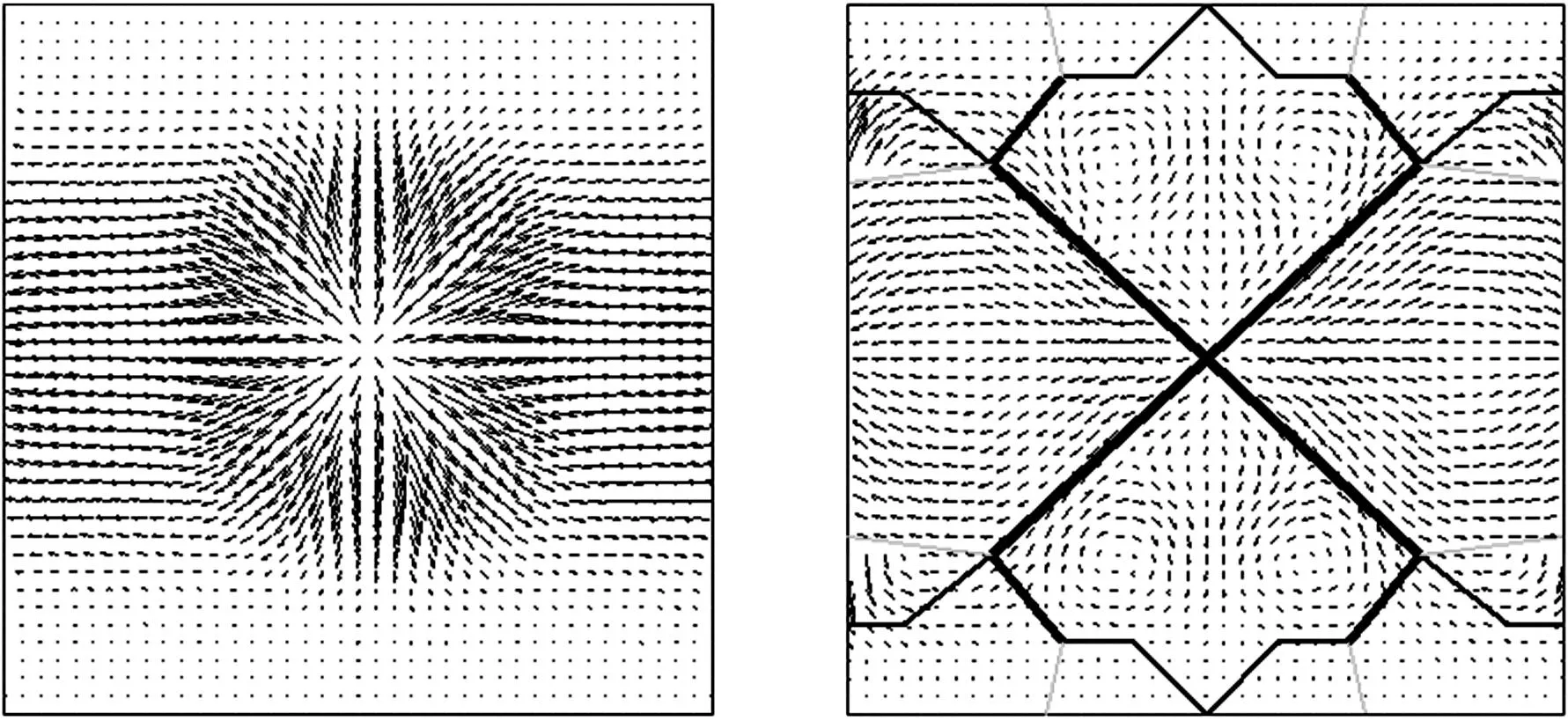
(a)原型薄板结构 　 　　(b) 仿脉序加筋板结构图5　结构声强矢量图

3.2对边固支带孔方板

正方形薄板边长L=0.4 m，厚度为0.04 m，板的中心开有直径d=0.1 m的圆孔，对边固支，如图6a所示。加强筋主脉初始宽度dm0=0.006 m，初始高度hm0=0.01 m，次脉初始宽度为主脉的一半，初始高度与主脉相同，主脉体积约束量为0.2V0，次脉体积约束量为0.1V0。简谐激励力分别反向作用于左右边界的中点，幅值Fa=1 N，材料的弹性模量E=210 GPa，泊松比μ=0.3，声速c=342 m/s，空气密度ρa=1.21 kg/m3，声功率参考值W0=10-12W，优化频段范围ω为0～1200 Hz。

根据主脉种子选取的“弹性应变能最小准则”，主脉种子设置在四个角点以及载荷作用处，主脉从边界种子出发向圆孔自由边界生长，次脉由主脉分歧生长，最后连接至固支边界。化简加强筋的原始布局，拟合原始脉络和修正脉序分歧处的截面尺寸，获得加强筋仿生脉序的最终分布构型。主脉在中部区域相对较粗，在分歧出其他脉络后，脉络截面处尺寸逐渐变小，主脉与次脉分布规整，适于机械加工。与相同体积约束下正交加筋布局方式相比(图6b～6d所示)，仿生结构的声辐射功率最大值为69.81 dB，低于正交加筋结构的最大值76.23 dB；从整个优化频率范围来看，仿生结构的声辐射功率平均值为49.85 dB，也低于正交加筋解的声辐射功率平均值54.56 dB，因此仿生结构能够更有效地降低声辐射功率，提高薄板的声辐射性能，如图7所示。

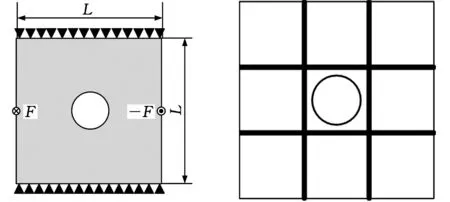
(a)对边固支带孔方板　 　 　(b)正交加筋板结构

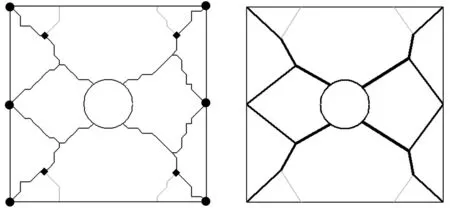
(c)仿脉序加筋计算构型 　 (d)仿脉序加筋光滑构型图6　薄板结构加筋布局方式对比

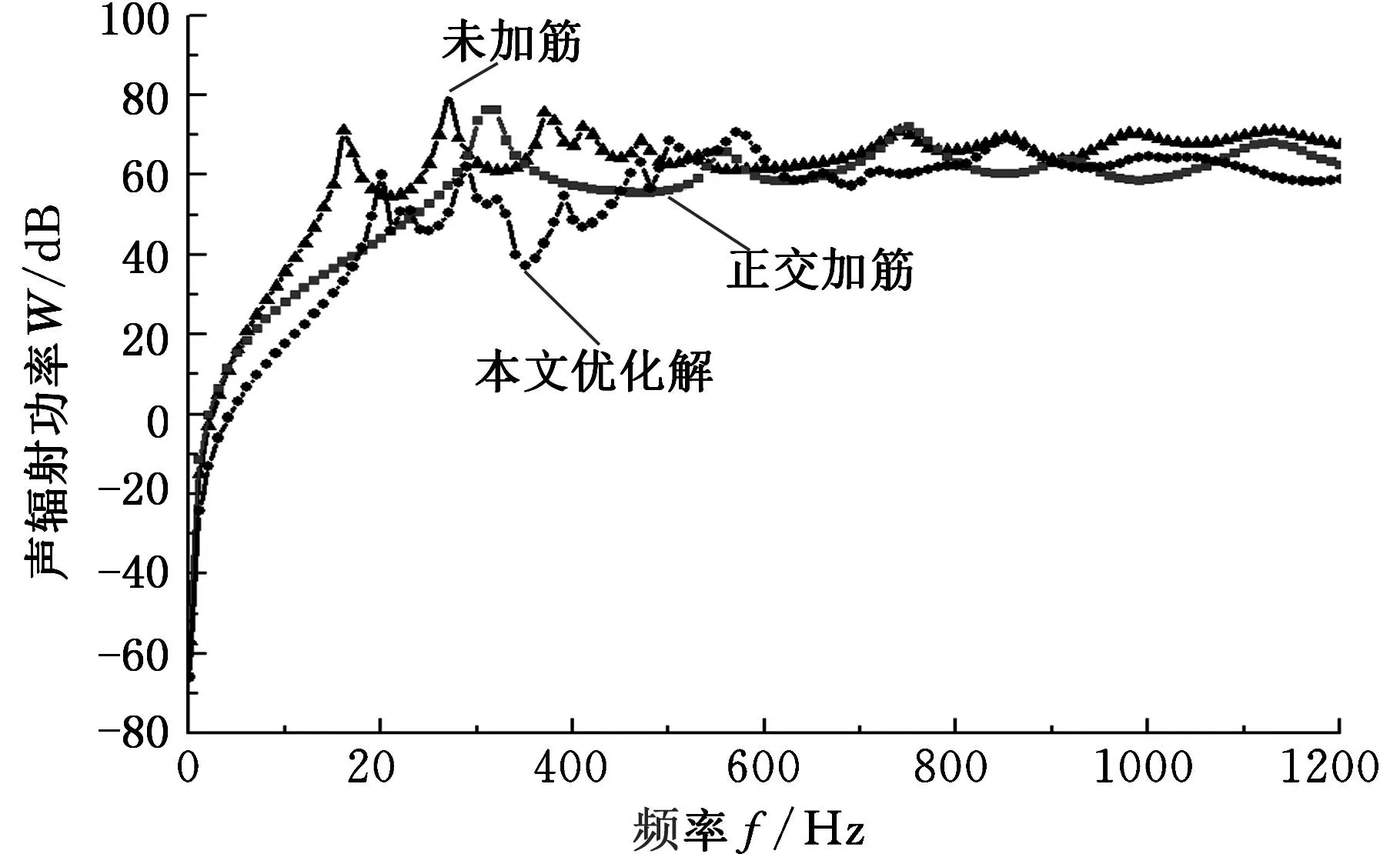
图7　声辐射功率对比

原型薄板结构由于是对边固支的边界条件，振动能量从自由边上的激励源流向圆孔方向，在靠近固支边的区域，振动能量分布较为稀疏，如图8a所示。仿生结构从激励源流出的能量一部分像原型结构那样朝着圆孔方向流动，同时受到加强筋形成的“围墙”的限制，振动能量必须沿着加强筋的方向流至圆孔的周围，孔的两侧聚集了更多的振动能量，而穿过加强筋的振动能量十分稀少；另一部分从激励源流出的能量在遇到加强筋的障碍之后，只得沿上下两个方向流回至自由边界而无法越过加强筋进行传递，如图8b所示。

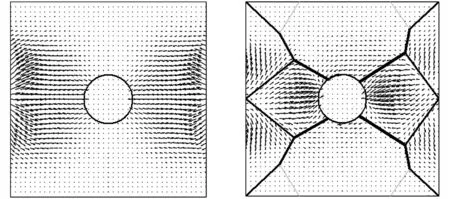
(a)原型薄板结构 　 　　(b) 仿脉序加筋板结构图8　结构声强矢量图

4结论

借鉴植物叶脉分枝结构分布形态的最优性原理，提取了植物脉序生长和分歧的力学准则，建立了仿脉序分布加强筋板梁耦合结构的仿生模型。以降低谐振结构声辐射功率为设计目标，提出了薄板减振降噪的仿生拓扑优化方法。通过结构声强理论分析了仿生结构的振动功率流特性，研究了结构的振动能量分布和传输特性。基于上述研究内容，获得如下结论：

(1)同体积约束下，仿脉序分布加筋板结构在优化频带内的声辐射功率显著低于正交加筋板结构的声辐射功率，仿生结构具有更优的减振降噪性能，验证了薄板结构低噪声仿生拓扑优化算法的有效性。

(2)除激励源处以外，主脉处功率流最大，次脉次之，随着离开激励点距离的增大而逐渐衰减。加强筋的存在，相当于在板上施加了一个沿筋连续分布的线激励，加强筋的存在改变了薄板中功率流的分布特性，主脉的刚度大，距离激励点近，由激励源提供的能量主要向加强筋主脉传递。

(3)加强筋分布主次分明，仿生布局具有更优的质量与刚度分布，结构降噪效能增强显著，而且适于机械加工。把仿生布局优化方法应用于复杂形状薄壁结构件的加筋布局设计问题，对典型板壳结构的工程应用将提供一定的理论与技术支撑。

综上，通过对谐振板壳结构振动声辐射的加强筋布局优化研究和对加筋板结构中振动能量传递、分布规律的研究，验证了本文所提出的仿生优化方法能够在实现结构轻量化的同时更为有效地降低结构振动的声辐射，并且布局结果适于加工，可以应用于工程实际中的一些板壳结构的声学优化问题。

参考文献：

[1]陈炉云, 张裕芳. 基于功率流分析的结构声优化研究[J]. 振动与冲击, 2010, 29(10): 191-194.

ChenLuyun,ZhangYufang.StructuralAcousticOptimizationBasedonPowerFlowAnalysis[J].JournalofVibrationandShock, 2010, 29(10): 191-194.

[2]陈炉云, 张裕芳, 李英辉. 肋骨分布对肋板声辐射影响及分布优化分析[J]. 武汉理工大学学报, 2011, 35(1): 24-28.

ChenLuyun,ZhangYufang,LiYinghui.AcousticRadiationInfluenceofStiffenersLayoutandLayoutOptimizationAnalysis[J].JournalofWuhanUniversityofTechnology, 2011, 35(1): 24-28.

[3]BojczukD,SzteleblakW.OptimizationofLayoutandShapeofStiffenersin2DStructures[J].ComputersandStructures, 2008, 86(13/14): 1436-1446.

[4]BojczukD,MrózZ.TopologicalSensitivityDerivativeandFiniteTopologyModifications:ApplicationtoOptimizationofPlatesinBending[J].StructuralandMultidisciplinaryOptimization, 2009, 39(1):1-15.

[5]杜建镔, 宋先凯, 董立立. 基于拓扑优化的声学结构材料分布设计[J]. 力学学报, 2011, 43(2): 306-315.

DuJianbin,SongXiankai,DongLili.DesignofMaterialDistributionofAcousticStructureUsingTopologyOptimization[J].ChineseJournalofTheoreticalandAppliedMechanics, 2011, 43(2): 306-315.

[6]DuJB,OlhoffN.TopologicalDesignofVibratingStructureswithRespecttoOptimumSoundPressureCharacteristicsinaSurroundingAcousticMedium[J].StructuralandMultidisciplinaryOptimization, 2010, 42(1): 43-54.

[7]史冬岩, 孔令成, 石先杰, 等. 弹性边界板结构拓扑优化声辐射[J]. 振动测试冲击与诊断, 2014, 34(1): 179-184.

ShiDongyan,KongLingcheng,ShiXianjie,et.al.SoundRadiationandTopologyOptimizationofPlateswithElasticBoundary[J].JournalofVibration,Measurement&Diagnosis, 2014, 34(1): 179-184.

[8]ArezkiB.AnIntroductiontotheMechanicsofMorphogenesisforPlantBiologists[J].TrendsinPlantScience, 2010, 15(6): 353-360.

[9]FrancisC,MokhtarAB,ArezkiB.InSilicoLeafVenationNetworks:GrowthandReorganizationDrivenbyMechanicalForces[J].JournalofTheoreticalBiology, 2009, 259(3): 440-448.

[10]丁晓红, 林建中, 山崎光悦. 利用植物根系形态形成机理的加筋薄壳结构拓扑优化设计[J]. 机械工程学报, 2008, 44(4): 201-205.

DingXiaohong,LinJianzhong,YamazakiKoestu.TopologyDesignOptimizationofStiffenedThin-wallShellStructuresBasedonGrowthMechanismofRootSystem[J].ChineseJournalofMechanicalEngineering, 2008, 44(4): 201-205.

[11]丁晓红, 陈建来, 程莉. 抗振板壳结构的仿生拓扑优化方法[J]. 船舶力学, 2008, 12(1): 125-130.

DingXiaohong,ChenJianlai,ChengLi.ABionicApproachofTopologyDesignOptimizationforVibration-proofPlateandShellStructures[J].JournalofShipMechanics, 2008, 12(1): 125-130.

[12]JiJ,DingXH,XiongM.OptimalStiffenerLayoutofPlate/ShellStructuresbyBionicGrowthMethod[J].ComputersandStructures, 2014, 35(4): 88-99.

[13]岑海堂, 陈五一. 小型翼结构仿生设计与试验分析[J]. 机械工程学报, 2009, 45(3): 286-290.

CenHaitang,ChenWuyi.StructuralBionicsDesignandExperimentalAnalysisforSmallWing[J].ChineseJournalofMechanicalEngineering, 2009, 45(3): 286-290.

[14]刘良宝, 陈五一. 基于叶脉分枝结构的飞机盖板结构仿生设计[J]. 北京航空航天大学学报, 2013, 39(12): 1596-1600.

LiuLiangbao,ChenWuyi.StructuralBionicDesignforAircraftCoverPlateBasedonLeafVeinBranchedStructure[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(12): 1596-1600.

[15]薛开, 李永欣. 板壳结构加筋布局的仿生脉序生长算法[J]. 哈尔滨工程大学学报, 2011, 32(9): 1262-1266.

XueKai,LiYongxin.ABionicVenationGrowthAlgorithmforaStiffenerLayoutinPlate/ShellStructure[J].JournalofHarbinEngineeringUniversity, 2011, 32(9): 1262-1266.

[16]LiBT,HongJ,WangZL,etal.AnInnovativeLayoutDesignMethodologyforStiffenedPlate/ShellStructuresbyMaterialIncreasingCriterion[J].JournalofEngineeringMaterialsandTechnology, 2013, 135(2): 021012-1-11.

[17]CorsonF,HenryH,Adda-BediaM.AModelforHierarchicalPatternsunderMechanicalStresses[J].PhilosophicalMagazine, 2010, 90(1/4): 1-18.

[18]BohnS,AndreottiB,DouadyS,et.al.ConstitutivePropertyofTheLocalOrganizationofLeafVenationNetworks[J].PhysicalReviewE, 2002, 65(6): 061914-1-1.

(编辑苏卫国)

A Bionic Approach of Topology Optimization to Low Noise for Thin Plates

Teng Xiaoyan1Jiang Xudong2Shi Dongyan1

1.Harbin Engineering University, Harbin, 1500012.Harbin University of Science and Technology, Harbin, 150034

Abstract：Aimed at minimizing the acoustic radiation power of thin plates for noise reduction, a bionic approach of topology optimization was presented to address stiffeners layout of thin plates by co-opting the characteristic configuration of botanic venation branched structures. A primary vein growth of stiffeners was governed by minimal strain energy while a secondary vein growth of ones by releasing maximal shear stress. At each junctions, leaf veins were adjusted according to the general Murray criterion. Consequently an adaptive growth algorithm of stiffeners was established featured with hierarchical structure like leaf vein. Exemplifying the transverse bending vibration and resulting acoustic radiation for clamped thin plates, the acoustic radiation power and the distribution of vibrational power flow were analysed respectively for thin plates with stiffeners layout imitating botanic venation. The numerical results show that the stiffeners layout method to imitating botanic venation is superior to the orthogonal stiffeners layout method in vibro-acoustic characteristics subjected to the same volume constraints for stiffeners. Therefore the bionic layout method of stiffeners to noise reduction is valid or feasible for thin plates.

Key words：bionic design; stiffer layout; topology optimization; thin plate structure; low noise

收稿日期：2015-07-16

基金项目：国家自然科学基金资助项目(51505096);黑龙江省自然科学基金资助项目(E2015026);中央高校基本科研业务费专项资金资助项目(HEUCF150701);黑龙江省青年科学基金资助项目(QC2016056)

中图分类号：TB532

DOI：10.3969/j.issn.1004-132X.2016.10.013

作者简介：滕晓艳，女，1980年生。哈尔滨工程大学机电工程学院讲师。研究方向为结构振动与拓扑优化。江旭东，男，1977年生。哈尔滨理工大学机械动力工程学院讲师。史冬岩，女，1965年生。哈尔滨工程大学机电工程学院教授。