二次通用旋转组合设计及最优化法在转杯纺工艺优化上的应用

薛志俊

(盐城工业职业技术学院，江苏 盐城 224005)

二次通用旋转组合设计及最优化法在转杯纺工艺优化上的应用

薛志俊

(盐城工业职业技术学院，江苏 盐城 224005)

文章运用二次通用旋转组合设计试验方案，运用MATLAB计算转杯纺工艺各因子与质量指标的回归系数，得出影响因子与质量指标之间的有效回归方程。建立目标函数后，利用最优化法求得相对合理的最优工艺。以棉/羊绒/绢丝70/15/15 18.5tex转杯针织纱为例，介绍了二次通用旋转组合设计方法在转杯纺工艺优化中的应用。

MATLAB；通用旋转；最优化法；工艺优化。

1 前言

在转杯纺生产过程中，由于纤维的成纱过程作用机理复杂，纱线性能受多种因素影响，很难得出生产工艺与质量指标的函数关系方程。本文运用二次通用旋转组合设计和最优化法，对转杯纺的转杯转速、分梳辊转速和设计捻系数三个关键工艺参数进行优化。应用MATLAB建立工艺参数与质量指标之间的回归方程，并对回归方程和回归方程系数的显著性进行检验，得出有效回归方程，最后利用随机方向搜索法得出最优工艺。

2 试验设计

将纺杯转速、分梳辊转速以及设计捻系数作为三个因子，参考实际生产经验以及相关资料[1]，最终确定三个因子的上下限分别为：

纺杯转速X1：50000～70000rpm；分梳辊转速X2：5000～6500rpm；设计捻系数X3：340～410。

根据二次通用旋转试验组合设计安排试验，因子水平编码见表1。

表1 三因子水平编码表

根据试验计划进行N=mc+2p+m0次试验，其中mc是2p型全因子试验或部分实施法的试验次数，m0是中心点试验次数，p是因子数。对于三因子通用旋转组合设计，根据二次通用旋转组合设计的参数表，mc为8，m0为6，最终N=20。结构矩阵(X)如表2所示。

3 纺纱方案及结果

参考质量指标为条干CV%、单纱断裂强力、1克纱线结杂粒数和3mm毛羽数，具体纺纱方案及测试结果(矩阵y)如表3所示。

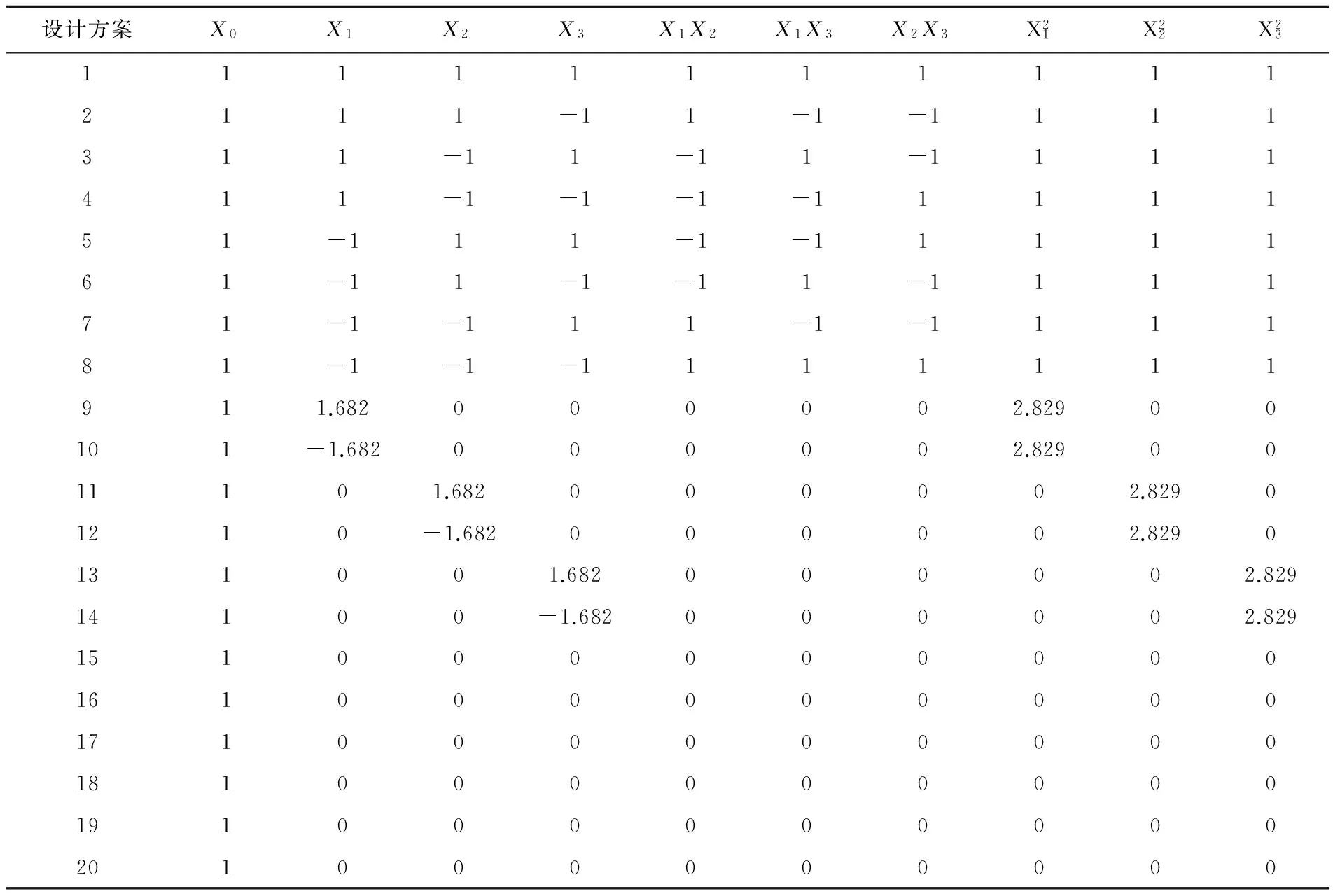
表2 三因子二次通用旋转组合设计结构矩阵表

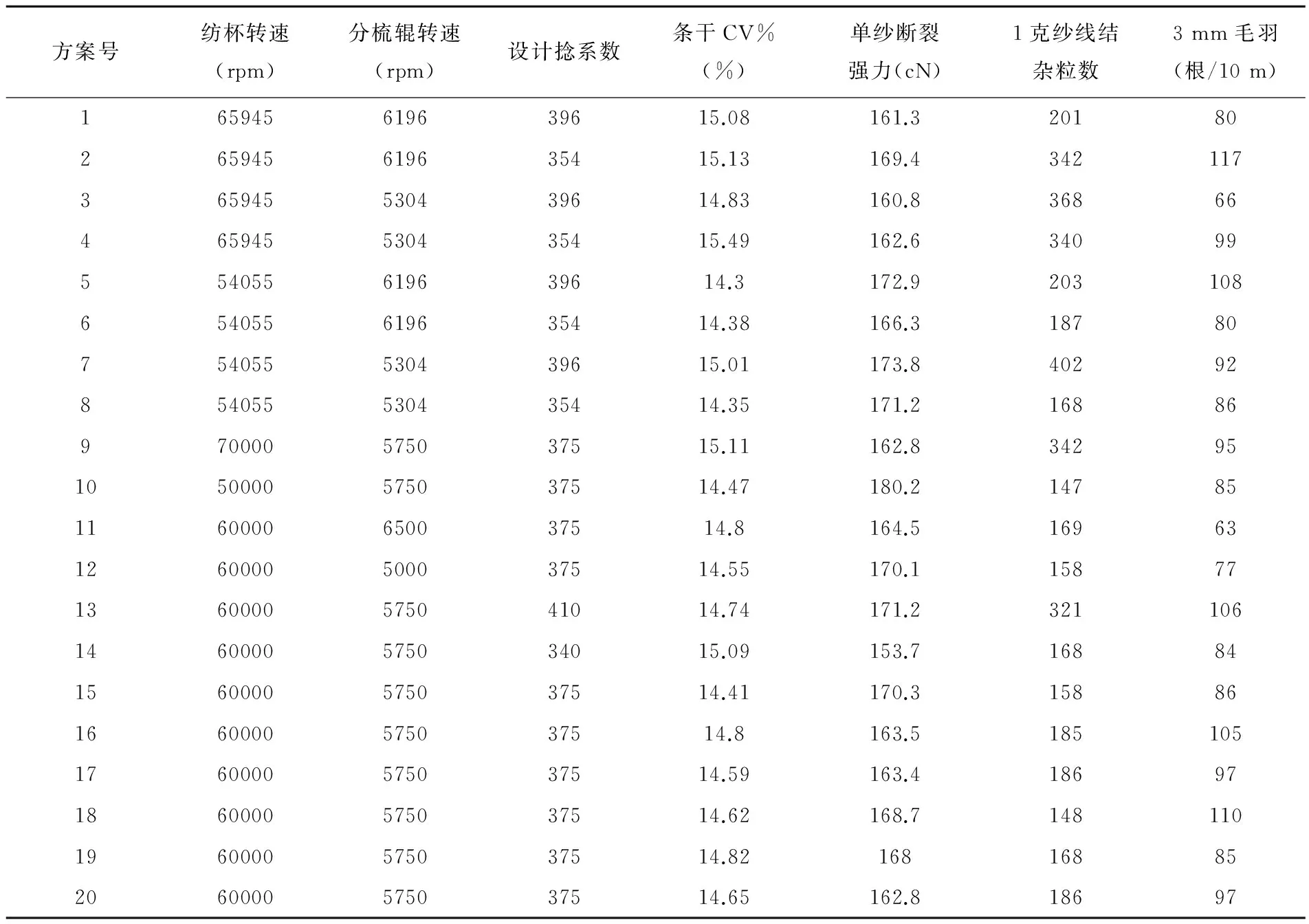
表3 纺纱方案及结果

4 回归方程的建立与最优化求解

4.1 各项质量指标的回归系数

采用最小二乘法公式b=(X′X)-1(X′y)，求得各考察指标的回归系数如表4所示。

4.2 回归方程及回归系数的显著性检验

对回归方程进行失拟性和显著性检验，应用MATLAB提供的逆累加分布函数finv的计算值与统计量F1进行比较，如果用统计量F1进行检验的结果是显著的[2]，就要进一步考察原因，改变二次回归模型; 如果检验结果是不显著的，就要进一步用统计量F2对二次回归方程进行检验,如果用统计量F2进行检验的结果是显著的，说明所得到的二次回归模型是比较合适的。回归方程的显著性检验结果如表5所示。

对于剩余回归方程的系数进行显著性检验如表6所示。

表4 各指标的回归系数

表5 各指标的回归方程显著性检验

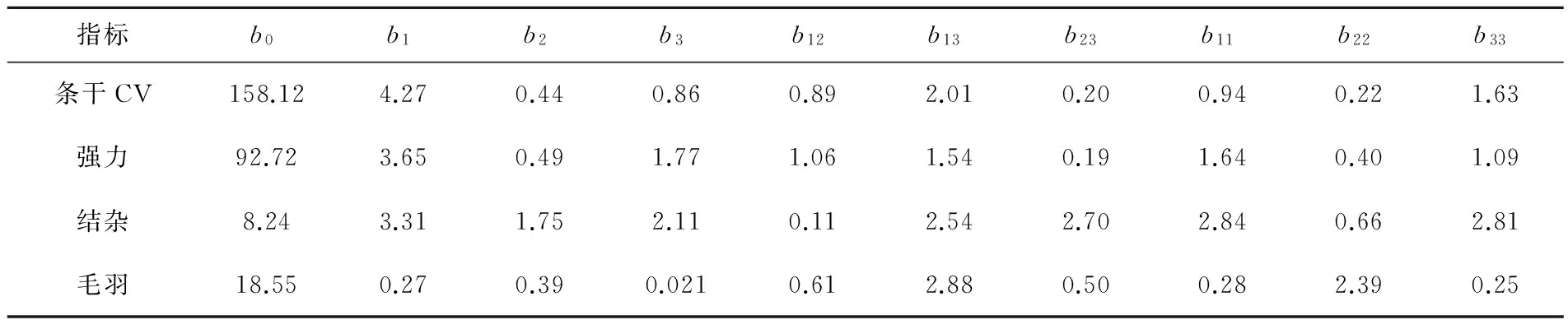
表6 剩余回归方程系数t值

5 有效回归方程及等高线分析

通过对剩余回归方程的系数进行显著性进行t检验，选用t0.15(10)=1.09为参考，剔除不显著的回归系数，最终的各指标的有效回归方程如表7所示。

表7 各指标的有效回归方程

利用MATLAB算法语言的图形处理功能，根据上述有效回归方程，可得到水平因子与质量指标之间的关系。

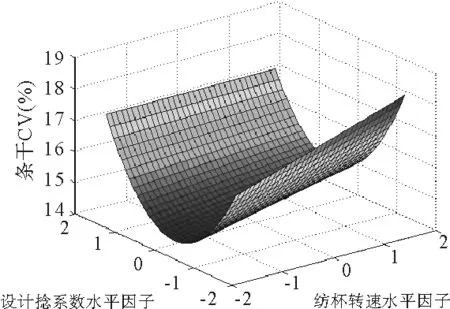
图1 条干CV%与纺杯速度、捻系数之间的关系

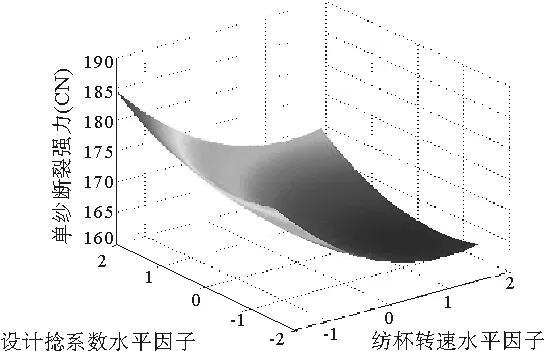
图2 断裂强力与纺杯转速、设计捻系数之间的关系

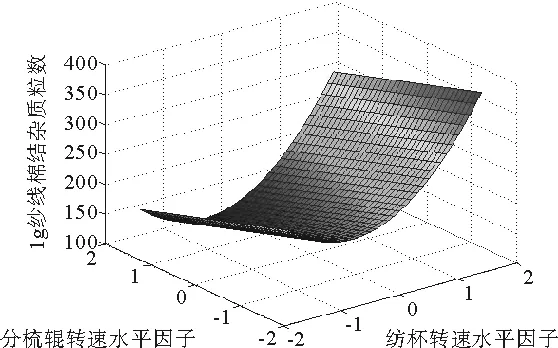
图3 结杂与纺杯转速、分梳辊转速之间的关系

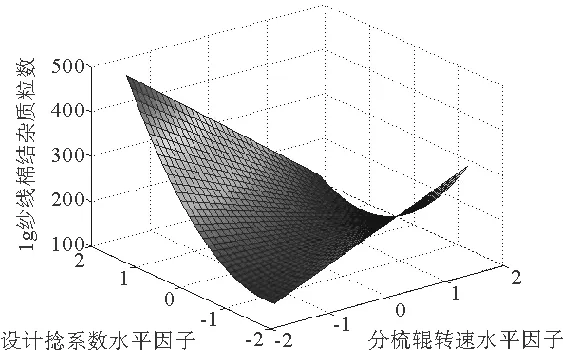
图4 结杂与捻系数、分梳辊转速之间的关系

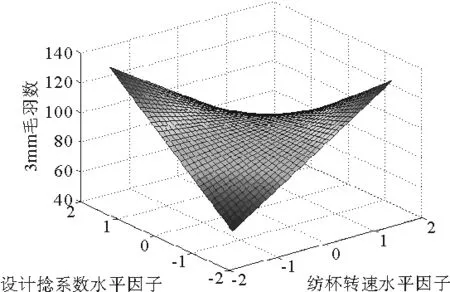
图5 毛羽与纺杯转速、设计捻系数之间的关系

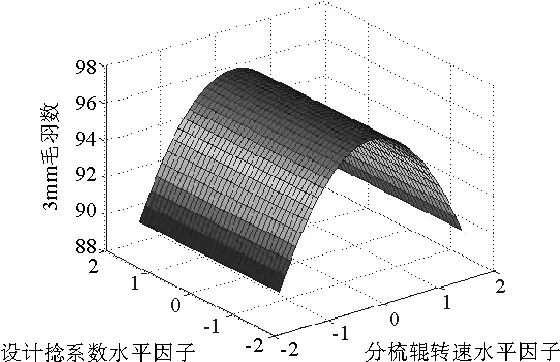
图6 毛羽与分梳辊转速之间的关系

图1表明随着转杯速度的增加,条干CV%值不断增大,纱线条干CV%随着捻系数的增加先减小后增大；图2表明纺杯速度越快，强力越低，设计捻系数越大，纱线强力越大；图3、图4表明纱线结杂受三个因素共同影响，纺杯速度越快，结杂越多，分梳辊速度越快，结杂越少，设计捻系数越大，结杂越多；图5、图6表明，增大设计捻系数可降低毛羽，纺杯速度增大，毛羽相应增大，分梳辊转速不断增大，毛羽先增大后减小。

6 工艺参数优化的数学模型及求解

利用MATLAB中的fmincon函数进行最优点搜索，选取条干CV%，单纱断裂强力、1g纱线棉结杂质粒数、3mm毛羽的极限值构建目标函数：

ff=(t1/14.3-1)2+(t2/180.2-1)2+(t3/147-1)2+(t4/63-1)2

ff越小，得出的方案越优。

采用MATLAB中随机方向搜索法程序进行求解，选择多次不同初始点进行求解，寻找最小的ff值，最终选用ff=0.0145,X1=-1.6781,X2=0.4151,X3=-1.4165,解码得纺杯转速为50023rpm，分数辊转速为5935rpm，设计捻系数为343。

7 结语

对比优化前后的纱线质量指标，如表8所示。

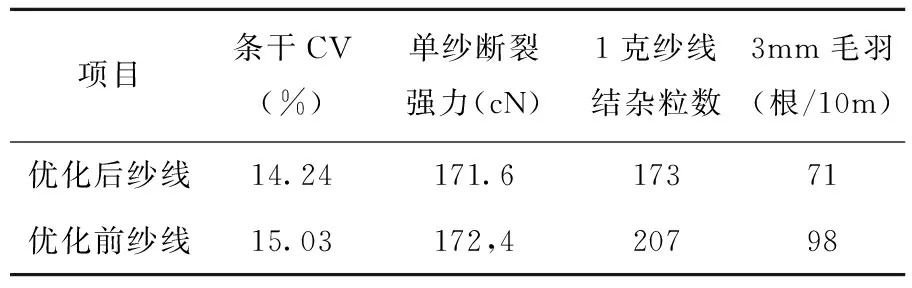
表8 优化前后纱线各项质量指标对比

从表8中可以明显看出，纱线的条干、结杂和毛羽性能明显提高，而强力相差不大，说明优化结果是可靠的。

[1] 胡玉才，李惠军.转杯纺三项工艺参数的优化组合对C32tex纱质量影响的研究[J].棉纺织技术，2008，36(1):7—10.

[2] 郁崇文等.工程参数的最优化设计[M].上海:中国纺织大学出版社,2003.

Apply Quadratic Regression Rotation Combination and the Best Method of Rotor Spinning Process Optimization

XueZhijun

(Yancheng Institute of Industry Technology, Yancheng 224005，China)

The scheme of Quadratic Regression Rotation Combination design and MATLAB to calculate the regression equation coefficient between rotor spinning process and quality were applied to draw an effective regression equation. Then the reasonable optimized process was calculated. Taken Cotton/Cashmere/Silk 70/15/15 18.4 tex as example, the method of Quadratic Regression Rotation Combination design applied in rotor spinning process optimization was introduced.

MATLAB; general rotary；optimization method; process optimization

2016-02-24

薛志俊(1971—)，男，江苏盐城人，副教授。

TS104.7+1

A

1009-3028(2016)02-0011-05