Experimental and numerical investigations of scale-up effects on the hydrodynamics of slurry bubble columns☆

Zhaoqi Li,Xiaoping Guan,Lijun Wang,Youwei Cheng,Xi Li

Department of Chemical and Biological Engineering,Zhejiang University,Hangzhou 310027,China

1.Introduction

Bubble columns are widely used for a variety of gas-liquid or gasliquid-solid reactions,including oxidation,hydrogenation,carbonyla tion,and Fischer-Tropsch synthesis.With the expansion of industrial processes,the largest diameter of commercial bubble columns has constantly grown up to 10 m in diameter.There is considerable interest,both within academia and industry,on scaling-up of bubbly reactors.During the past decades,numerous studies have been conducted for measurement and simulation of hydrodynamic behaviors of bubble column[1-13].But these investigations were restricted to low superficial gas velocity(VG＜0.3 m·s-1),small column size(D＜0.5 m),and no solid presence.In order to study the scale-up rules of bubble column,experimental and numerical investigations were further conducted in bubble columns of large diameter in the open literature.Tsutsumiet al.[14,15]used a hot-wire probe to detect the bubble behaviors and heat-transfer rate in bubble columns with diameters of 0.2,0.4 and 0.8 m,and set up an artificial neural network(ANN)model to predict the scale-up effect.Nottenkam peret al.[16]and Forettet al.[17,18]respectively used a wheel anemometer and Pavlov tube to detect liquid velocities in bubble columns with diameter up to 1.0 m to highlight the scale effect in slurry bubble columns.However,experimental data were still inadequate in large diameter columns(D＞0.5 m),and only the normalized pro files of liquid velocity were listed in most works.

Simulation of bubble column operated in the heterogeneous or churn-turbulent regime was much difficult due to significant coalescence and breakage of bubbles.Joshi and coworkers[19-24]adopted drift flux theory to model the pro file of gas holdup in bubble column by CFD solution of model equations.But some empirical parameters had to be determined in advance,including gas-liquid slip velocityVSand others.Krishna and coworkers[25-28]developed a two-class bubble model,in which bubble breakup and coalescence were expressed as the change of proportion of large and small bubbles.Olmoset al.[29],Chenet al.[30],Jakobsenet al.[31]and Bholeet al.[32]made use of the population balance model(PBM)to simulate the distribution of bubble size.The population balance model was more reasonable for understanding some special phenomena of bubble movements and formations,but it is too difficult to be solved so it is still impractical for the scale-up of commercial bubble columns under the current computing power.

In most CFD simulation works on gas-liquid and gas-liquid-solid flows in the literature,a constant bubble size was used in homogeneous regime.For churn-turbulent flow regime,most attention has been drawn to coupling the PBM into the CFD framework.Due to the high computational cost and difficulties in considering bubble deformation,breakup,and coalescence,the PBM-CFD model is difficult to be solved for commercial scale bubble columns.In this work a 2-D axisymmetric k-ε model simulation was conducted,in which an average bubble size was assumed in churn turbulent multi-phase flow.In the simulation,bubble size was determined by force balance between buoyance and drag force,and gas holdup pro files were determined by the balance between the lateral lift force and the turbulent diffusion force.In addition,a liquid-solid system was regarded as a pseudo homogeneous mixture,and effects of solid concentration were considered as the variation of average bubble size.In order to verify the capability of the model in predicting the effects of scale,superficial gas velocity and solid concentration,plenty of experiments in a wide range of superficial gas velocities(0.12-0.62 m·s-1)and solid concentrations(0-30 vol%)were conducted in bubble columns of0.2 m,0.5 m,and 0.8 m diameter.

2.Experimental Section

2.1.Experimental setup

To determine the sensitivity of hydrodynamic characteristics to column diameter and to be able to predict their quantitative extent,measurements were performed in different columns with the column diameter as large as possible.In the present work,we used three columns with internal diameter D=0.2 m,0.5 m and 0.8 m(Fig.1).

Experiments were conducted at ambient temperature and atmospheric pressure with the air/water system.A 30 mm thick per forated plate distributor with 2.5 mm holes uniformly distributed was placed at the bottom of the column.The percentages of open area of the distrib utor are controlled within 1% foreach bubble column so that aircould be bubbled into the columns continuously and uniformly.Provision was made on the column wall for mounting the conductivity probe and Pavlov tube at two different positions above the distributor.The gas flow-rates were measured and controlled using a set of pre calibrated rota meters and needle valves.superficial gas velocities were regulated in the range of 0.12-0.62 m·s-1.Tap water and glass beads were added into columns in advance.The average particle size of solid particles is 100 μm,and solid concentrations were regulated from 0%to 30%by weight.The dispersed slurry height was measured by a ruler,and the clear slurry height was obtained using a side tube.

2.2.Measurement of local gas holdup

An electrical resistivity probe(conductivity probe)was used to measure local gas holdup in the bubble column.It was made of an IC Ni-Cr alloy wire(diameter of0.15 mm)and coated with insulating material to the tip.The probe was fixed to a stainless steel support tube elbow as shown in Fig.2.The data were acquired by a computer with a 16-bit A/D converter card.The data was acquired at a sampling frequency of 2000 Hz for 60 s.The acquired conductivity data time series were subjected to noise removal and phase discrimination,using Labview.A typical signal obtained was shown in Fig.3,in which high voltage was detected when the probe was submerged in liquid but low voltage when the probe was in contact with bubbles.A phase discrimination threshold was set to filter the bubble signals,and the threshold magnitude of10%of the max voltage was set from the comparison of the signal achieved using the probe with the average gas holdup estimated from bed expansion.

Fig.1.Schematic views of the bubble column of(a)0.8 m,(b)0.5 m and(c)0.2 m i.d.

Fig.2.Structure of the conductivity probe.

Fig.3.Typical conductive signal for the measurement of local gas holdup.

2.3.Measurement of local liquid velocity

Local liquid velocities are measured by a Modified Pavlov tube(o.d.6 mm,openings 1 mm)based on the literature works[33,34,18].The structure of the Modified Pavlov tube is shown in Fig.4.The ΔPmeasuring time for each acquisition is 3 min with a frequency of 135 Hz.The instantaneous liquid velocity uiand the time-averaged velocityVlwere calculated in line with a revised formulation considering the influence of gas hold-up[35,36]:

in whichK,called the momentum conversion factor,can be regressed by a calibration experiment asK=1.56/(1+0.5αS),andJ=1+ εGis the momentum exchange factor[34].Furthermore,the root mean square(r.m.s.)velocity uσwas calculated as

Fig.4.Structure of the Pavlov tube.

3.CFD Model for Heterogeneous Bubbly Flow

In the bubble column,gas bubbles appear to move towards the column centric region while rising upwards.The determination of the gas holdup pro file is a key difficulty for the simulation of heterogeneous bubbly flow.Besides the drag force,other two forces,namely lateral lift force and turbulent dispersion force,have great influence on the radial pro files of gas holdup in heterogeneous flow[24].Therefore,they were introduced for the computation of gas-liquid equations of motion in the CFD model,despite that there was a dispute regarding the magnitude and even the sign of them[37].

The influence of solid concentration was considered as follows.Firstly,in the range of experimental conditions investigated in this work,spatial pro files of the solid concentration are much uniform.The liquid-solid system in the bubble column could be treated as a pseudo-homogeneous mixture[38-40].Secondly,many experiments indicated that solid concentration mainly influences on the gas holdup.Some authors[41-44]believed that the addition of solid concentration leads to an increase in bubble size,which is attributed to an increase in the apparent suspension viscosity.However,predicting the effect of apparent viscosity on the bubble size is much difficult in CFD simulations,unless bubble coalescence/breakage is considered.In view of the complexity of the description of bubble coalescence/breakage,a simpler method was adopted for the consideration of the effect of solid concentration in the work:An average bubble size was assumed and estimated according to experimentally observed average gas holdup,and then the effect of solid concentration was equivalent to the variation of the average bubble diameter.

3.1.Interface force terms

·Drag force:Schiller and Naumann's formula was used in the work[45]

where Reynolds'number is de fined asRe=dB|ul-ug|ρl/μl,anddBis the bubble size.

·Lift force:The radial force depends upon bubble rotation around its own axis,relative gas-liquid velocity and a liquid velocity gradient,viscous and turbulent shear gradients,radial pressure gradients,bubble shape changes,wake phenomena and the coalescence tendency.The lateral lift force may be expressed as[19]

whereCLis the lift coefficient.Joshi[19]recommended that the lift coefficient should be regarded as an adjustable parameter to match experimental results.In order to match the experimentally observed gas holdup pro file at superficial gas velocity ranging from 0.12 to 0.62 m·s-1in the bubble columns of 0.2-0.8 m diameter,we regarded the lift coefficient as a function of local phase holdup,and expressed as

·Turbulent dispersion force:The turbulent dispersion force is also important for the determination of radial pro files of gas holdup.The turbulentdispersion force was proposed by Lopez[46]based on analogy to molecular dynamics:

whereCTDis the force coefficient,andkis the liquid turbulent kinetic energy per unit of mass.CTDwas determined as a constant value 2.2 resulted from a good fitting for the present experimental data of overall gas holdup at superficial gas velocity ranging from 0.12 to 0.62 m·s-1.

3.2.Governing equations

In this work,a 2-D axisymmetric two- fluid Eulerk-ε model is used.According to the literature works[47-49,19],the equations of continuity and motion for ther-zcylindrical coordinate system are summarized in Table 1.

Table 1Governing equations of axisymmetric k-ε model for bubbly flows

The value of parametersCμ,σk,σε,Cε,1,andCε,2came from the standardk-ε equations,which are respectively 0.09,1.0,1.3,1.44 and 1.92.In the model,bubble size is assumed as uniform which is determined by force balance between buoyance and drag force

Slip velocity is assumed by average gas holdup

While average gas holdup is computed by the correlation given by Wanget al.[13]

3.3.Simulation strategy and conditions

The above given conservation equations were solved by a finite volume method by a commercialCFD code,FLUENT 6.2.16(Ansys Inc.,US),in double precision mode.The pressure-velocity coupling was resolved using the SIMPLE algorithm.The grids are created by GAMBIT 2.2.30 and exported into FLUENT.To getrid of dependence of discretization resolution,different sets of grids were tried.Fig.5 shows the radial pro files of time-averaged axial liquid velocities computed with different numbers of grids at superficial gas velocity 0.31 m·s-1in a 0.8 m diameter column.Eventually,it was determined that about 100×1000 cells were sufficient and effective in all of the investigated situations.

Fig.5.Radial pro files of time-averaged axial liquid velocities computed with differentsets of grids.

The initial and boundary conditions were set as follows.For the gas phase at the inlet the velocity-inlet boundary condition was used,while the pressure-outlet boundary condition was applied on the outlet.Initially the column was filled with liquid up to the level that matches the static liquid height measured in the experiment.To prevent liquid escape from the column the computational domain in the axial direction was about 50%-80%higher than the static liquid height.The additional terms of lift force,turbulent dispersion force were imbedded in the FLUENT code with user-de fined subrout ines(UDFs).Transient CFD simulations were carried out using a time step of 1×10-3s.Generally it took about half an hour in a 64 core work station to reach the quasisteady state(1×105-2×105time steps)when almost all physical parameters didn't change with time.

4.Results and Discussion

The experimental findings and their comparison with the CFD simulation were discussed in this section.All measurements are performed in fully developing region to get rid of the influence of the gas distributor,about1 times diameter at leastabove the gas distributor and 1 times diameter below the free surface.The simulations were performed for all experimental conditions.Hydrodynamic rules on the scaling-up and effects of superficial gas velocity and solid concentration were revealed.

4.1.Flow field

The most important characteristics of the flow field in bubble columns are the radialgas holdup pro file and the intense liquid circulation.Fig.6(a)presented a liquid velocity vector graph obtained from the CFD simulations in a 2Daxisymmetric coordination ata superficialgas velocity of0.31 m·s-1in the column of0.8 m i.d.Although,the instantaneous liquid recirculation in a bubble column is very complex and visually seems to be quite chaotic,the time-averaged liquid flow seemed to be quite regular:an upward flow in the center of the column and a downward flow near the wall.In addition,the gas velocity vector graph was presented in Fig.6(b).It can be found that,there is almost no downward gas flow in the column even near the wall.

Fig.6.Distributions of flow properties at superficial gas velocity of 0.31 m·s-1 in the column of 0.8 m i.d.(a)Vector-graph of liquid velocity(m·s-1);(b)vector-graph of gas velocity(m·s-1);(c)contours of gas holdup;(d)contours of turbulent kinetic energy(m2·s-2);(e)contours of turbulent viscosity(Pa·s-1).

The pro files of time-averaged gas holdup obtained from the CFD simulations are shown in Fig.6(c).Higher gas holdups occur in the center of the column,but lower near the wall.At the vicinities of gas sparger and free surface,a complex graphic is shown owing to the recirculating flow in these areas.In the bubble column, fluid is driven by density difference induced by radial non-uniform pro files of gas holdup,and proper prediction of gas holdup pro files is the key point for obtaining a stable solution of the CFD model.The lift force makes bubbles gathered at the center of the column;otherwise the turbulent dispersion homogenizes the gas holdup gradient.Simulations indicated that the gas holdup pro file is sensitive to the selection of force coefficientsCLandCTD.

Furthermore,Fig.6(d)and(e)provided typical pro files ofkand μtin the column,which are related with fluid mixing.In the fully-developing region,turbulent viscosity maximizes at the center of the column,and then gradually decreases towards the wall, finally quickly falls near the wall.Correspondingly,turbulent kinetic energy presents a dual peek distribution,whose maximum value occurs at a point(r/R=0.7)which is close to the inversion point of liquid recirculation velocity,where the maximum turbulent shear stress appears.Because thek-ε model is based on isotropic assumption,turbulent kinetic energy in the figures is constructed with a limitation that all the normal components of stresses are equal to each other.As a result,there may be some degree of deviations for the calculation of turbulent flow at anisotropic turbulent regions,such as the vicinities of gas sparger,free surface,and the wall.

4.2.Effect of superficial gas velocity

The superficial gas velocity is a dominant factor that affects hydrodynamic behaviors of the bubble column.As shown in Fig.7,the average gas holdup increases with the increase of the superficial gas velocity while pro files of gas holdup become steeper at high superficial gas velocity compared with the low velocity.The change of gas holdup profile could be explained by the radial force balance of the lift force and the turbulent dispersion force in the fully-developing region.As stated in Eq.(5),the lift force is related with the relative slip velocityVS.The appearance of large bubbles at high gas velocity results in the rising ofVSbetween gas-liquid phases.Thus,the increase of the lift force drives more gas bubbles towards the center of the column.

Fig.7.Radial pro files of gas holdup at different superficial gas velocities in the column of 0.8 m i.d.

The center-line liquid velocity ul(0)is a key parameter in describing the liquid circulation of bubble columns.Fig.8(a)shows that ul(0)increases strongly with superficial gas velocity.It is noted that ul(0)is higher than 1.3 m·s-1in the column of 0.8 m diameter atVG=0.62 m·s-1,more than twice the value of superficial gas velocity.Fig.8(a)also shows the comparisons of the hydrodynamic parameter in a large diameter column with literature results.The computational values of ul(0)in the column of 1 m diameter is in agreement with experimental data in[16]but about 20%lower than measurements in[17].In addition,liquid velocity pro files also become steeper with the increase of superficial gas velocities(Fig.8(b)).The flow reversal occurs at the dimensionless radial coordinate of about 0.7 under all investigated conditions.This result is in agreement with numerous authors[1,16,25].

Fig.9(a)provided computational pro files ofkat superficial gas velocities of 0.62 m·s-1in the column of 0.8 m i.d.by using different turbulent models.It could be seen that the average error is within 10%among them.Therefore,the commonly used standardk-ε model was chosen to investigate influences of operating conditions on hydrodynamics of bubble columns.

The measurements of r.m.s. fluctuation velocities in three coordinate directions were carried out in the work.Turbulent kinetic energykwas calculated in line with the summation of them.Fig.9(b)provided profiles ofkat five superficial gas velocities of 0.12,0.19,0.31,0.47,and 0.62 m·s-1in the column of 0.8 m i.d.As shown in the figure,turbulent kinetic energy is lowest at the wall,and then rises rapidly inwards the column.at the inversion of liquid velocity,a maximum value is reached,thenkgradually falls and flattens at the column axis.As shown in the figure,kincreases with superficial gas velocities.The centric value ofkreaches 0.5 m2·s-2at the superficial gas velocity of0.62 m·s-1,while it is only 0.16 m2·s-2for the superficial gas velocity of 0.12 m·s-1.

Fig.8.Effects of superficial gas velocities on time-averaged axial liquid velocities in the column of 0.8 m i.d.(a)Variation of the center-line liquid velocities at different superficial gas velocities;(b)radial pro files of time-averaged axial liquid velocities at different superficial gas velocities.

Fig.9.Radial pro files of turbulent kinetic energies in the column of 0.8 m i.d.(a)Comparisons of different turbulent models at superficial gas velocity of 0.62 m·s-1;(b)comparisons between standard k-ε model and experimental results at different superficial gas velocities.

Fig.10.Effects of column scales on gas holdups.(a)Variation of average gas holdup with super ficial gas velocities in columns of different sizes;(b)radial pro files of gas holdups in columns of different sizes at superficial gas velocities of 0.62 m·s-1.

4.3.Effect of column diameter

To investigate the scaling effect of the bubble column,experiments were conducted in three different columns with diameters of 0.2 m,0.5 m and 0.8 m i.d.Fig.10(a)shows that average gas holdups are very close in all columns,that is,the averaged gas holdup is slightly affected by column size.The curve plotted in the figure seems to be an appropriate correlation for fitting experimental data,which was obtained by Wanget al.[13].Pro files of gas holdup at a superficial gas velocity of 0.62 m·s-1in three columns were showed in Fig.10(b),in which the pro files of gas holdup in the columns of 0.5 m and 0.8 m i.d.are quite similar,but different with the column of 0.2 m i.d.Pro file of gas holdup in the smallest column is steeper than others,perhaps due to the wall effect.This trend follows the same similar pro file found early by Forretet al.[17]based on experiments performed on three columns of 0.15 m,0.4 m,and 1 m i.d.

Comparing the center-line liquid velocities in columns of different sizes(Fig.11(a)),it could be found that the liquid recirculation velocities enhanced with the growth of column size.For example,the centric liquid velocity reached 1.3 m·s-1in the column of 0.8 m i.d.at a superficial gas velocity of 0.62 m·s-1,but only 1.0 m·s-1in the column of 0.2 m i.d.Zehner's[2]and Nottenkamper's[16]correlation and the CFD of our work provided a good agreement with experimental results than Riquarts'[50].The axial force balance of the liquid phase in the bubble column sheds more light on the understanding of the scalingup effect of the bubble column.In the fully-developing region,the axial momentum conservation equation of the liquid phase could be simplified as[51]

whereξ=r/Ris the non-dimensional radius.In Eq.(16),the influence of column sizes on the axial liquid velocity is mainly reflected in the term,μt/R2.Fig.11(b)provided simulation results of turbulent viscosity μtin columns of different scales,which showed that μtis approximately proportionaltoR1.5.Therefore,It wasn'thard to conclude thatunless the change of gas holdup was considered,the radial pro file of timeaveraged axial liquid velocity was about 0.5 powers dependent on the column scale.

Fig.11.Effects of column scales on time-averaged axialli quid velocities and turbulent kinetic energies at the superficial gas velocities of0.62 m·s-1.(a)Prediction and comparison of the center-line liquid velocities between various publish models;(b)simulation results of turbulent viscosities in three columns.

Fig.12.Effects of column scales on turbulent kinetic energies atsu perficial gas velocities of 0.62 m·s-1 in three columns.

Fig.12 provided pro files of turbulent kinetic energies at the superficial gas velocities of 0.62 m·s-1in three columns.It can be seen thatkincreases with the growth of column scales.When variations of kinetic turbulent energy were correlated with column diameters,a power-law relationk∝R0.5was obtained.According to Eq.(7),the increase of turbulent kinetic energy with the growth of column scale homogenizes the gas holdup gradient.On the contrary,in view of Fig.11 and Eq.(5),the large gradient of liquid velocity with the growth of column scale enhances the lateral lift force,which results in the steep trend of the gas holdup pro file.Combination of the two factors leads to the insignificant dependence of gas holdup on column diameters.

4.4.Effect of solid concentration

Experiments showed that the main influence of the solid concentration lies in the change of gas holdup.Fig.13 provided radial pro files of gas holdup at four different solid concentrations in the column of 0.5 m i.d.It can be seen that averaged gas holdup decreases apparently with the increase of solid concentration.The reason For the decrease of gas holdup is that the addition of solid concentration expands the bubble size,which results in an increase in the bubble rise velocity.In addition,the curve shape of gas holdup pro files remains similar.

Fig.13.Effects of solid concentrations on radial pro files of gas holdup under conditions of superficial gas velocities of 0.62 m·s-1,four solid concentrations in the column of 0.5 m i.d.

Differencing from gas holdup,time-averaged axial liquid velocities remained almost unchanged with the increase of solid concentration(Fig.14).The reason for this discrepancy is that the driven force of liquid circulation,namely density difference of fluid,remains the same due to parallel shift of the gas holdup pro file.CFD simulations also indicated that the density of solid particles and the apparent viscosity of liquid solid mixture have only a slight effect on the time-averaged axial liquid velocity.

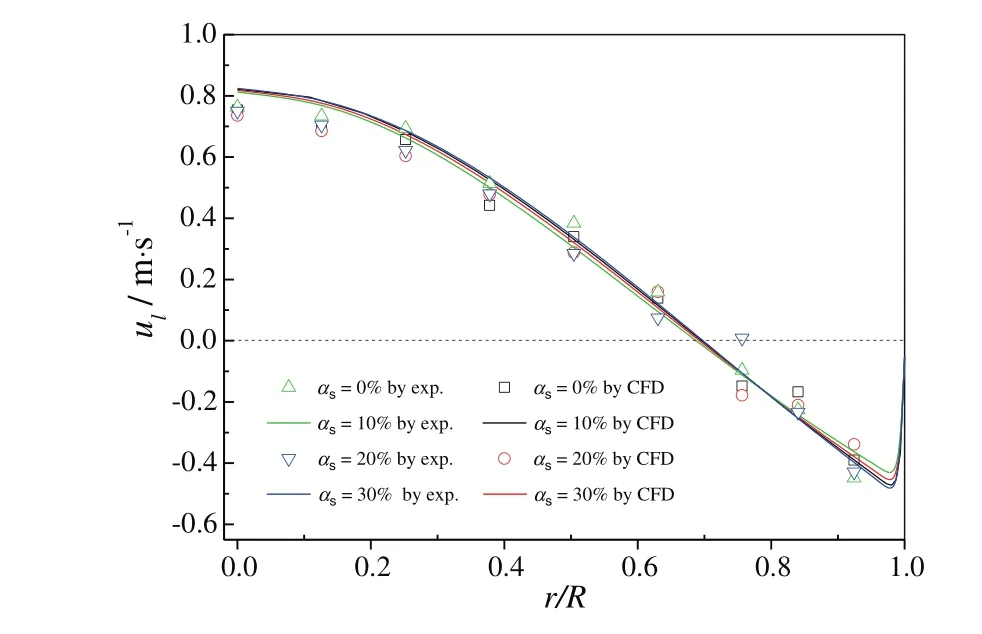
Fig.14.Effects of solid concentrations on radial pro files of time-averaged axial liquid velocities under conditions of superficial gas velocities of 0.62 m·s-1,four solid concentrations in the column of 0.5 m i.d.

5.Conclusions

Experiments and simulations were conducted for bubble columns with diameter of 0.2,0.5 and 0.8 m at high superficial gas velocities(0.12-0.62 m·s-1)and high solid concentrations(0-30 vol%).Some important findings and conclusions were obtained.

·The average gas holdup increases with the increase of the superficial gas velocity.Pro files of gas holdup become steep at high superficial gas velocity.Similarly,an identical trend was shown for timeaveraged liquid velocity and turbulent kinetic energy.

·The presence of solid in the bubble column would apparently inhibit the breakage of bubbles,which results in an increase in the bubble rise velocity and a decrease in the gas holdup.The curve shape of radial gas holdup pro files remains similar,and time-averaged axial liquid velocities were slightly affected by solid concentration.

·Scale-up rules of the bubble column are mainly due to variation of hydrodynamic parameters with column diameters.The axial liquid velocity remarkably increases in the core of columns with the larger column diameter,whereas the gas holdup is slightly affected.Turbulent kinetic energy increases with column scales.

Ourstudy reveals the scale-up rules on the hydrodynamics of bubble columns and shows the scale-up trends at high superficial gas velocities up to 0.62 m·s-1.However,due to the assumption of average bubble size in the CFD model,it is short of research and discussion when referring to bubble behaviors.

Nomenclature

CDdrag coefficient

CLlift coefficient

随着碳普惠相关研究近年来的不断升温，很多政府、企业尝试通过碳积分形式建立小范围的针对个人的碳普惠机制。但是，各类碳普惠机制在整体框架设计、碳减排量化方法、激励机制等层面并没有统一的理论指导，这为下一步不同碳普惠机制间的对接，以及未来碳普惠与碳交易市场的对接带来了诸多问题。

CTDdispersion force coefficient

Cμ,σk,σε,Cε,1,Cε,2,Cε,3parameters in standardk-ε model

Dcolumn diameter,m

dBbubble diameter,m

FDdrag force,N·m-3

FLlift force,N·m-3

FTDturbulent dispersion force,N·m-3

g gravity acceleration,m·s-2

Nnumber of experimental data

ppressure,Pa

ReReynolds number(=ρl|ug-ul|dB/μl)

tflow time,s

u velocity,m·s-1

VGsuperficial gas velocity,m·s-1

Vs slip velocity of gas-liquid phases,m·s-1

αgvolume fraction of gas phase

αlvolume fraction of liquid phase

αsmass concentration of solid

ε turbulent kinetic energy dissipation rate,m2·s-3

μtmixing turbulent viscosity,Pa·s-1

ρ density,kg·m-3

Subscripts

g gas phase

kphase index

lliquid phase

m mixture of gas-liquid phases

s solid phase

[1]J.H.Hills,Radial non-uniformity of velocity and voidage in a bubble column,Trans.Inst.Chem.Eng.52(1974)1-9.

[2]P.Zehner,Momentum,mass and heat transfer in bubble columns,Part 1:Flow model of the bubble column and liquid velocities,Int.Chem.Eng.26(1986)29-35.

[3]A.Lubbert,B.Larson,Detailed investigation of the multiphase flow in airlift tower loop reactors,Chem.Eng.Sci.45(1990)3047-3053.

[4]H.Luo,H.F.Svendsen,Turbulent circulation in bubble columns from eddy viscosity distributions of single-phase pipe flow,Can.J.Chem.Eng.69(1991)1389-1394.

[5]B.P.Yao,C.Zheng,H.E.Gasche,H.Hofmann,Bubble behavior and flow structure of bubble columns,J.Chem.Eng.Process Technol.29(1991)65-75.

[6]J.S.Groen,R.G.C.Oldeman,R.F.Mudde,H.E.A.Van,Coherent structures and axial dispersion in bubble column reactors,Chem.Eng.Sci.51(1996)2511-2520.

[7]A.A.Kulkarni,J.B.Joshi,V.R.Kumar,B.D.Kulkarni,Simultaneous measurement of hold-up pro files and inter facial area using LDA in bubble columns:predictions by multiresolution analysis and comparison with experiments,Chem.Eng.Sci.56(2001)6437-6445.

[8]J.M.Schweitzer,J.Bayle,T.Gauthier,Local gas hold-up measurements in fluidized bed and slurry bubble column,Chem.Eng.Sci.56(2001)1103-1110.

[9]S.Degaleesa,M.P.Dudukovic,Y.Pan,Experimental study of gas-induced liquid- flow structures in bubble columns,AIChE J.47(2001)1913-1931.

[10]U.Parasu Veera,K.L.Kataria,J.B.Joshi,Effect of superficial gas velocity on gas holdup pro files in foaming liquids in bubble column reactors,Chem.Eng.J.99(2004)53-58.

[11]L.A.Briens,N.Ellis,Hydrodynamics of three-phase fluidized bed systems examined by statistical,fractal,chaos and wavelet analysis methods,Chem.Eng.Sci.60(2005)6094-6106.

[12]M.R.Rampure,A.A.Kulkarni,V.V.Ranade,Hydrodynamics of bubble column reactors at high gas velocity:Experiments and computational fluid dynamics(CFD)simulations,Ind.Eng.Chem.Res.46(2007)8431-8447.

[13]L.J.Wang,Y.Zhang,X.Li,Studies on hydrodynamics of slurry turbulent bubble column(I)gas holdup and its radial distribution,CIESC J.59(2008)2996-3002(in Chinese).

[14]A.Tsutsumi,W.Chen,T.Hasegawa,et al.,Neural networks for prediction of the dynamic heat-transfer rate in bubble columns,Ind.Eng.Chem.Res.40(23)(2001)5358-5361.

[15]A.Tsutsumi,R.Kikuchi,Design and scale-up methodology for multi-phase reactors based on non-linear dynamics,Appl.Energy67(1)(2000)195-219.

[16]R.Nottenkamper,A.Steiff,P.M.Weinspach,Experimental investigation of hydrodynamics of bubble columns,Ger.Chem.Eng.6(1983)147-155.

[17]A.Forret,J.M.Schweitzer,R.Gauthier,et al.,Scale up of slurry bubble reactors,Oil Gas Sci.Technol.61(2006)443-458.

[18]A.Forret,J.M.Schweitzer,R.Gauthier,et al.,influence of scale on the hydrodynamics of bubble column reactors:an experimental study in columns of 0.1,0.4 and 1 m diameters,Chem.Eng.Sci.58(2003)719-724.

[19]J.B.Joshi,Computational flow modeling and design of bubble column reactors,Chem.Eng.Sci.56(2001)5893-5933.

[20]J.B.Joshi,V.S.Vitankar,A.A.Kulkarni,et al.,Coherent flow structures in bubble column reactors,Chem.Eng.Sci.57(2002)3047-3053.

[21]M.T.Dhotre,K.Ekambara,J.B.Joshi,CFD simulation of sparger design and height to diameter ratio on gas hold-up pro files in bubble column reactors,Exp.Thermal Fluid Sci.28(2004)407-421.

[22]K.Ekambara,M.T.Dhotre,J.B.Joshi,CFD simulations of bubble column reactors:1D,2D and 3D approach,Chem.Eng.Sci.60(2005)6733-6746.

[23]A.A.Kulkarni,K.Ekambara,J.B.Joshi,On the development of flow pattern in a bubble column reactor:development of a 3D CFD code and verification with results from LDA measurements,Chem.Eng.Sci.62(2007)1049-1072.

[24]M.V.Tabib,S.A.Roy,J.B.Joshi,CFD simulation of bubble column—an analysis of inter phase forces and turbulence models,Chem.Eng.J.139(2008)589-614.

[25]R.Krishna,J.M.Van,M.I.Urseanu,Three-phase Eulerian simulations of bubble column reactors operating in the churn-turbulent regime:A scale-up strategy,Chem.Eng.Sci.55(2000)3275-3286.

[26]R.Krishna,J.M.Van,Eulerian simulations of bubble columns operating at elevated pressures in the churn turbulent flow regime,Chem.Eng.Sci.56(2001)6249-6258.

[27]R.Krishna,J.M.Van,Scaling up bubble column reactors with highly viscous liquid phase,Chem.Eng.Technol.25(2002)1015-1020.

[28]J.M.Van,R.Krishna,Eulerian simulations for determination of the axial dispersion of liquid and gas phases in bubble columns operating in the churn-turbulent regime,Chem.Eng.Sci.56(2001)503-512.

[29]E.Olmos,C.Gentric,C.Vial,et al.,Numerical simulation of multiphase flow in bubble column reactors.influence of bubble coalescence and breakup,Chem.Eng.Sci.56(2001)6359-6365.

[30]P.Chen,M.P.Dudukovic,J.Sanyal,Three-dimensional simulation of bubble column flows with bubble coalescence and breakup,AIChE J.51(2005)696-712.

[31]H.A.Jakobsen,H.Lindborg,C.A.Dorao,Modeling of bubble column reactors:progress and limitations,Ind.Eng.Chem.Res.44(2005)5107-5151.

[32]M.R.Bhole,J.B.Joshi,D.Ramkrishna,CFD simulation of bubble columns incorporating population balance modeling,Chem.Eng.Sci.63(2008)2267-2282.

[33]J.Reimann,H.Kusterer,H.Jhon,Two-phase mass flow rate measurements with Pitot tube and density measurements,Symp.Measuring Techniques in Gas-Liquid Two-phase Flows,Nancy,France,1983.

[34]T.H.Lee,G.C.Park,D.J.Lee,Local flow characteristics of subcooled boiling flow of water in a vertical concentric annulus,Int.J.Multiphase Flow28(8)(2002)1351-1368.

[35]Z.Li,L.Wang,X.Li,Experimental and numerical investigations of bubble column under large diameter,high superficial gas velocity,244th National Fall Meeting of the ACS,Philadelphia,USA,2012.

[36]Y.Zhang,L.Wang,X.Li,Studies on hydrodynamics of turbulent slurry bubble column(II):axial liquid and slurry velocity distribution,CIESC J.59(12)(2008)3003-3008(in Chinese).

[37]H.A.Jakobsen,Chemical Reactor Modeling:Multiphase Reactive Flows,Springer,Berlin Heidelberg,2008.

[38]R.Krishna,J.M.Van,M.I.Urseanu,etal.,Design and scale up of a bubble column slurry reactor for Fischer-Tropsch synthesis,Chem.Eng.Sci.56(2)(2001)537-545.

[39]J.M.Van,J.Ellenberger,R.Krishna,Scale-up strategy for bubble column slurry reactors using CFD simulations,Catal.Today79(2003)259-265.

[40]T.F.Wang,J.F.Wang,Y.Jin,Experimental study and CFD simulation of hydrodynamic behaviours in an external loop airlift slurry reactor,Can.J.Chem.Eng.82(6)(2004)1183-1190.

[41]J.F.Brady,Computer simulation of viscous suspensions,Chem.Eng.Sci.56(2001)2921-2926.

[42]T.F.Wang,J.F.Wang,Y.Jin,Slurry reactors for gas-to-liquid processes:A review,Ind.Eng.Chem.Res.46(2007)5824-5847.

[43]C.O.Vandu,K.Koop,R.Krishna,Large bubble sizes and rise velocities in a bubble column slurry reactor,Chem.Eng.Technol.27(2004)1195-1199.

[44]G.Q.Yang,B.Du,L.S.Fan,Bubble formation and dynamics in gas-liquid-solid fluidization—a review,Chem.Eng.Sci.62(2007)2-27.

[45]L.Schiller,A.Naumann,A drag coefficient correlation,Vdi Ztg.77(318)(1935)51.

[46]B.M.Lopez,Turbulent Bubbly Two-phase Flow in a Triangular Duct(Ph.D.Thesis)Rensselaer Polytechnic Institute,New York,1992.

[47]H.B.Stewart,B.Wendroff,Two-phase flow models and methods,J.Comput.Phys.56(1984)363-409.

[48]H.A.Jakobsen,B.H.Sannaes,S.Grevskott,et al.,Modelling of vertical bubble-driven flows,Ind.Eng.Chem.Res.36(1997)4052-4074.

[49]A.Sokolichin,G.Eigenberger,A.Lapin,Simulation of buoyancy driven bubbly flow:established simplifications and open questions,AIChE J.50(2004)24-45.

[50]H.P.Riquarts,Strömungspro file,impulsaustausch und durchmischung derflüssigen phase in blasensäulen,Chem.Ing.Tech.53(1981)60-61.

[51]P.Gupta,B.Ong,M.H.Al-Dahhan,et al.,Hydrodynamics of churn turbulent bubble columns:Gas-liquid recirculation and mechanistic modeling,Catal.Today64(2001)253-269.