智能机床的误差补偿技术*

郭云霞，叶文华，梁睿君，何 磊

（南京航空航天大学机电学院，南京 210016）

郭云霞

博士研究生，研究方向为智能数控装备技术。发表学术论文10余篇，并参与国家自然科学基金资助项目相关课题研究。

在“工业4.0”和“中国制造2025”战略双重背景的驱动下，数控机床正朝着高端、智能、绿色的方向发展。智能机床是机床行业关注的热点，在零件加工过程中能够智能辅助决策、自动感知、智能监测、智能控制和智能维护,实现加工过程优质、高效、低能耗多目标优化运行[1]。

随着航空、航天、汽车、能源、电子、生物医疗等领域的快速发展，对机床加工精度的要求越来越高。机床精度提高的方法有误差防止法和误差补偿法。通过提高机床各零部件设计、制造和装配水平来减小或消除误差的方法是误差防止法,这种提高机床制造精度的“硬”技术成本高[2]。误差补偿法是预设一种新误差去抵消或减小偏离目标值的机床误差，即通过测量、分析、统计等方法分析出机床误差的特点和规律，建立误差数学模型，使预设的新误差抵消或减小加工过程中产生的误差[3]。这是一种提高机床加工精度的“软”技术，也是一种超越性技术，它能使零件的加工精度高于机床本身的精度，而投入的费用远远低于采用“硬”技术所需的费用，并将成为提高未来机床精度的一种主要方法。

目前，国外一些主要机床及数控系统厂商已经研发出误差补偿技术并应用于实际产品中。如日本大隈机床开发了5轴控制机床的几何误差补偿与精度维持智能化系统；马扎克的智能机床中融入智能热屏障技术，它通过热变形补偿技术与主轴冷却装置的共同作用，使得加工精度长时间保持稳定[4]；瑞士米克朗研发的高速主轴智能温度漂移控制（ITC）是一种温度补偿系统，可根据主轴温度变化情况，在加工中进行实时热补偿。在国内，华中数控研发的智能数控系统中的智能补偿模块是由激光干涉仪对机床空间误差进行测量，建立空间误差模型进行补偿；大连光洋科技研制的NC60/61数控系统也具有几何误差和热误差补偿功能。

智能机床误差补偿技术总体框架

智能机床误差补偿技术借助各类传感器对机床加工精度的影响因素（如工作环境、加工参数等）进行智能检测、智能感知及智能决策，并借助大数据平台实时地对数据信息进行智能分析、融合与处理，能准确得出误差补偿数值实时补偿。该技术进一步提高了误差补偿的自动化程度，为达到更高的补偿精度、更快的补偿速度、更好的补偿实时性的理想目标奠定基础。

在智能机床误差补偿系统中，除了对机床的几何误差进行补偿外，还要对加工过程中由热、力、振动等引起的误差进行补偿。加工过程中热、力、振动信号可分别通过温度传感器、力传感器、加速度传感器或其他间接采集方法进行实时采集；加工过程中或加工过程间的零件误差可通过零件在线测量或在机测量系统进行测量与计算得到。误差补偿系统根据预先建立的误差模型和实时采集的数据，经系统分析计算得到误差补偿量，进而补偿误差。整个补偿过程脱离人为干涉因素，系统自行进行最优化补偿方案。智能机床误差补偿系统总框架如图1所示。

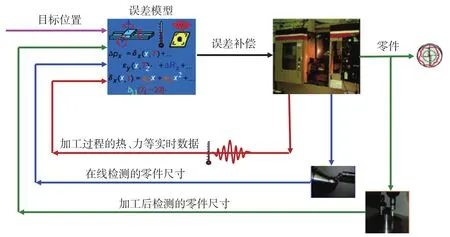
图1 智能机床误差补偿系统Fig.1 Error compensation system for intelligent machine tool

目前，对机床准静态误差（包括几何误差和热误差）的补偿研究相对比较成熟，对力误差等动态误差的补偿研究还属于起步阶段。机床准静态误差补偿技术主要包括误差检测、误差元素辨识与分离、误差建模和补偿控制这几个方面。机床准静态误差补偿过程如图2所示。

机床误差源及误差元素分析

智能机床误差主要包括几何误差、热误差与力误差（图3），控制误差相对较小，通常已由数控系统内部进行补偿，在此不做讨论。

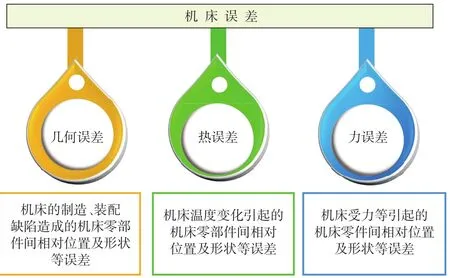
图3 机床误差及主要误差源Fig.3 Errors and main error resources of machine tool

几何误差主要来源于数控机床零部件制造与装配误差，是与机床零部件形状和位置精度相关的一类误差。在机床部件进行移动或转动时，这些位置和形状误差会叠加到机床的运动部件上，进而导致几何误差的产生[5]。同时，机床运动部件在内、外部热源作用下会产生热变形，在切削力等其他力的作用下会产生力变形。机床热变形和力变形都使其运动轨迹偏离理想运动轨迹，产生热误差和力误差。机床的几何误差元素、热误差元素、力误差元素都包括移动副误差元素、转动副误差元素以及主轴误差元素。

根据运动学原理，一个刚体由6个自由度（包括3个移动自由度和3个转动自由度）来确定它在空间的位置和方向，因此，机床的每个移动副或转动副都分别有3个移动误差δ和3个转角误差ε，而3个移动轴相互之间还存在垂直度误差S，3个转动轴相互之间还存在平行度误差η；机床主轴旋转时，会产生3个移动误差和2个转角误差，因此，具有3个移动轴（T轴）和2个转动轴（R轴）的五轴联动机床共有42项几何误差元素、42项热误差元素和42项力误差元素。

各轴的基本误差元素见表1，表中δuv、εuv分别表示沿坐标轴u和绕坐标轴v的移动误差、转角误差，其中下标u代表误差方向X、Y、Z，下标v表示坐标轴运动方向X、Y、Z、A、B、C、S。通常把δuv、εuv称为基本误差元素。机床的误差元素可以表示为、，其中上标W表示误差源，其中误差源包括G（几何误差）、T（热误差）、F（力误差），例如移动几何误差、转动热误差。

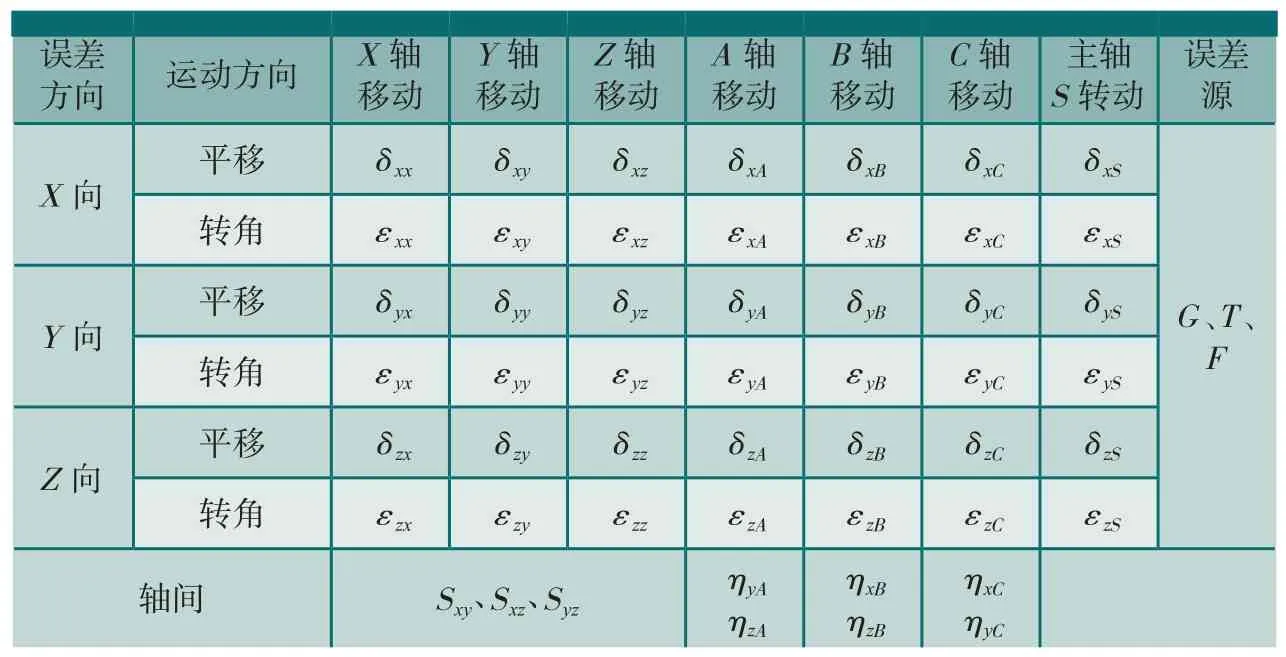
表1 基本误差元素表

几何与热误差建模

建立一套准确反映机床误差的模型是误差补偿的关键。误差建模可分为误差元素建模和综合误差建模。前者通过对机床几何误差、热误差等特性辨识建立模型，用来预测误差值；后者将预测的误差值分配到各运动轴上，用于进行补偿。

1 误差元素模型

在误差补偿系统中，误差不同采用的建模方法也不同。如几何误差元素是仅与机床位置有关的误差元素，热误差元素是与温度有关的误差元素，复合误差元素是与机床位置和温度都有关的误差元素，其建模方法各异。

（1）几何误差元素建模。

影响机床几何误差的因素较多，且具有非线性，精确建模困难。目前，几何误差元素建模最常用的方法是基于最小二乘法的回归建模法，依据刚体假设，使用机床运动轴位置坐标的多项式模型来拟合几何误差元素，求得几何误差元素的模型。其他常用的方法包括齐次坐标变换法、正交多项式建模法、神经网络法、多体系统理论法、遗传算法等[6-9]。

（2）热误差元素建模。

热误差元素建模原理与几何元素建模原理类似，其影响因素较几何误差更为复杂。通常依据统计理论对相关误差数据进行分析，将热误差元素表达为机床温度的多元函数，再由最小二乘及回归原理拟合建模，得到仅与温度有关的机床热误差元素的数学模型。

在误差元素建模中，神经网络模型是热误差建模的典型方法之一。它有着较强的对非线性模型的预测能力，基于人工神经网络的准静态热误差模型能够较好地预测机床的热误差，但模型的辨识参数缺乏实际的物理意义，它对非训练工况下的预测结果有待验证。所以，很多学者将遗传算法[10]、粒子群算法[11]、灰色理论[12]融入了BP 神经网络，并将其作为神经网络初值寻优的方法，使得预测结果进一步提高。

除了传统意义上的神经网络与多元回归分析，热误差的建模还应用独立成分分析[13]、支持矢量回归[14]、支持向量机[15]、贝叶斯网络[16]、投影寻踪回归[17]等方法，进一步提高建模精度[18]。

（3）复合误差元素建模。

复合误差元素建模过程比较复杂，先要进行几何误差和热误差的分离，然后各自建模，最后再将两种误差元素模型合成一个复合误差元素模型。

几何误差和热误差的分离如图4所示[19]。其中，几何误差是在机床冷态时测得；热误差与机床上某些点的温度有关，可对每次测得的一组误差数据进行直线拟合，各误差曲线一次拟合线的斜率即为其各数值。

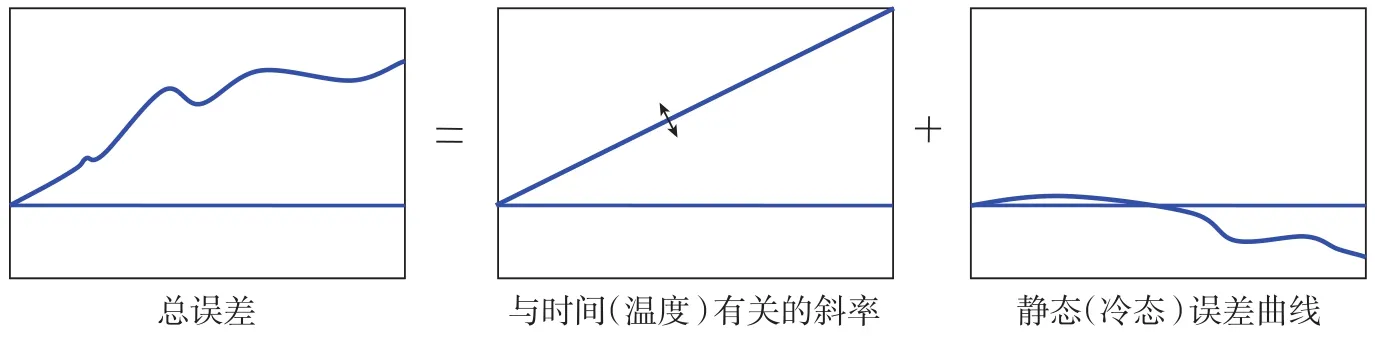
图4 几何误差和热误差分离示意图Fig.4 Separation diagram of geometric error and thermal error

2 误差综合模型

数控机床的运动结构可归结为两条开式运动链：一条为从刀具、主轴到床身之间的“刀具－床身”运动链；另一条为从工件到床身之间的“工件－床身”运动链。组成运动链的各个运动副是移动副或转动副，每个运动副分别对应机床的一个坐标轴。在床身上建立参考坐标系，在各轴上分别建立子坐标系，形成两条运动链间的位姿关系，由矩阵运算把多维空间中的一个点集从一个坐标系变换到另一个坐标系，可得到综合误差模型[20]。以典型旋转五轴RTTTR型龙门机床CXYZA为例（图5），其具体步骤为：

（1）建立各运动轴、主轴、床身等系列坐标系。如图6所示，CXYZA型五轴联动机床总体运动链可表示为：T→S→A→Z→Y→X→R←C←W。其中，“刀具运动链”包含R在内的左半部分，表示刀具到床身的坐标系变换；“工件运动链”包含R在内的右半部分，表示工件到床身的坐标系变换。

图5 五轴CXYZA龙门机床结构示意图Fig.5 Structure diagram of five-axis CXYZA gantry machine tool

图6 五轴机床坐标系Fig.6 Coordinate system of five-axis machine tool

（2）根据齐次坐标变换原理，建立误差转换矩阵。在理想状态下，工件坐标系W到刀具坐标系T的坐标变换为：

式中，T为坐标变换矩阵；T右侧上标i为理想状态；T左侧上标、右侧下标代表从左上标坐标系到右下标坐标系的变换。

在实际存在误差的状态下，工件坐标系W到刀具坐标系T的坐标变换为：

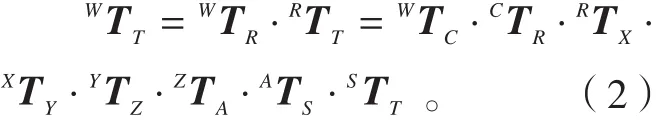
（3）建立工件和刀具坐标系之间的运动关系，获得误差模型。工件坐标系W到刀具坐标系T的变换矩阵在实际状态下可看作是在理想情况下复映上一个误差运动矩阵WET[21]，即

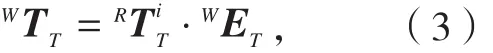
求解WET可得误差的综合模型：

近年来，补偿中的建模方法层出不穷，但要注重建模方法的可行性，实现模型的可移植性，以及多误差综合建模的耦合性。应继续深入研究和理解机床中误差产生原因及规律，建立简化和实用的模型，进行预测和补偿，并使其处于可控状态。

几何与热误差补偿

根据误差元素模型、误差综合模型和实时检测的温度、位置等数据，补偿系统预测的机床最终误差，在补偿过程中进行实时补偿。综合补偿的主要方式是反馈干涉法和原点平移法。

1 反馈干涉法

反馈干涉法补偿原理如图7所示[20]，编码器的反馈信号由补偿计算机获得，并依据误差综合模型得出机床的空间误差，将等同于空间误差的脉冲信号与编码器的反馈信号相比较，控制系统据此实时调节工作台的位置。

图7 反馈干涉法补偿原理Fig.7 Diagram of feedback disruption compensation principle

2 原点平移法

原点平移法补偿原理如图8所示[20]。机床的空间位置误差由补偿计算机进行计算得出，并将误差量送至CNC控制器，利用机床控制系统的原点偏移功能，将补偿信号加到伺服环的控制信号中，进而实现误差量补偿。

图8 原点平移法补偿原理Fig.8 Diagram of origin shifting compensation principle

目前，上述两种补偿方法只能在部分配置高档数控系统的机床上实现，近年来也不断涌现出新型补偿技术，例如基于传递函数的热误差补偿技术、热亲和补偿技术以及基于大数据思维的误差补偿技术等。事实上还迫切需要开发具有经济性、智能性、方便性、通用性的误差补偿系统，同时和机床生产厂家合作，共同推进补偿研究的进步和完善。

力误差补偿技术

力误差是一种附加误差。在加工过程中，零件受切削力、夹紧力、惯性力等作用破坏了机床各组成部分原有的相互位置关系，导致零件产生几何变形。其中影响最大的是切削力。对航空航天等制造领域常见的弱刚性薄壁零件，切削力引起的零件变形已成为加工精度提高的主要难题，对这类零件的力误差补偿技术研究是未来智能机床的一个重要方向。

零件切削变形误差补偿的基本思路是计算切削变形量，采用反向变形补偿法，通过修改或调整NC程序实现补偿，其关键是切削变形量的计算。切削变形估算目前主要有两种方法（如图9所示）。一种是基于切削力测量的方法，即预先建立切削力与零件变形之间的关系模型，再根据由测力仪直接测量获得或通过测量主轴电机电流后经计算得到的切削力，来计算零件切削变形量。另一种是基于有限元仿真分析的方法，即先采用完全经验模型、基于切削试验的机械力模型、基于切削机理的物理模型、基于人工智能的神经网络模型等切削力建模方法建立表征切削参数与切削力关系的切削力模型，计算切削力；然后再采用有限元分析方法进行仿真计算，得到由切削力引起的零件切削变形。

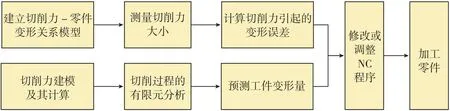
图9 切削变形误差补偿流程Fig.9 Cutting deformation error compensation process

基于零件在线测量的误差综合补偿技术

基于零件在线测量的误差综合补偿是指利用机床在线测量系统对测得的工件误差进行误差补偿的技术，它可对由机床几何误差、热变形、力变形及其他因素引起的零件误差进行综合补偿。

基于零件在线测量的误差综合补偿过程如图10所示。机床在线测量系统测量工件加工表面，得到工件表面几何轮廓，通过与零件CAD模型比对，计算出零件误差，采用反向变形补偿法自动生成或调整NC加工程序完成误差补偿。

图10 基于零件在线测量的误差综合补偿流程Fig.10 Error synthetic compensation process based on online measurement of parts

总结与展望

机床误差补偿技术涉及误差测量、建模与补偿3个方面。目前，智能机床误差补偿技术的研究还处于起步阶段，虽然几何误差与热误差补偿方法研究已比较深入，但实际应用才刚刚开始；而力误差的补偿研究还处于探索阶段，由于力误差涉及零件加工过程，目前主要是针对特定零件加工过程进行切削力建模、变形测量与计算、NC程序生成与调整等方面研究，还没有开展力误差实时补偿及其与机床控制系统集成等方面的研究。基于零件在线测量的误差补偿技术能对几何误差、热误差、力误差及其他误差进行综合补偿，但测量与补偿精度受机床本身精度的限制，同样也难以进行误差实时补偿。因此，智能机床误差补偿技术将来的重点，一方面是要研究包括力误差和装夹误差等在内的其他误差的实时补偿技术，另一方面要研究几何误差、热误差、力误差及其他误差的一体化综合补偿技术。

[1] 张曙,机床产品创新与设计[M],南京: 东南大学出版社,2014.

ZHANG Shu,The innovation and design of machine tool products[M],Nanjing: Southeast University Press,2014.

[2] 盛晓尘,数控磨床热误差实时补偿控制系统研制及其应用[D],上海: 上海交通大学,2006.

SHENG Xiaochen,Rerearch and application of control system in the real-time thermal error compensation for CNC grinding machine[D].Shanghai : Shanghai Jiao Tong University,2006.

[3] 李永祥,数控机床热误差建模新方法及其应用研究[D].上海: 上海交通大学,2007.

LI Yongxiang,New methods of thermal error modeling for NC machine tools and their researchmend and application[D],Shanghai :Shanghai Jiao Tong University,2007.

[4] 张伟,智能制造与智能机床技术[J].金属加工(冷加工),2014(10)：13-15.

ZHANG Wei,Intelligent manufacturing and intelligent machine tool technology[J],Metal Working (Metal Cutting),2014(10)：13-15.

[5] 范开国.数控机床多误差元素综合补偿及应用[D].上海: 上海交通大学，2012.

FAN Kaiguo,Comprehencive compensation and application for multi-error elements onCNC machine[D],Shanghai: Shanghai Jiao Tong University,2012.

[6] 童恒超，杨建国，刘国良，等,机床导轨系统空间误差的齐次变换建模及应用[J].上海交通大学学报,2005,39(9): 1400-1403.

TONG Hengchao,YANG Jianguo,LIU Guoliang,et al,Homogeneous transformation modeling for volumetric errors of a machine tool guideway system and its applications[J],Journal of Shanghai Jiao Tong University,2005,39(9):1400-1403.

[7] RAKSIRI C,PARNICHKUN M.Geometric and force errors compensation in a 3-axis CNC milling machine[J],International Journal of Machine Tools & Manufacture,2004,44(12-13): 1283-1291.

[8] 沈金华,李永祥,鲁志政,等,数控机床几何和热误差综合实时补偿方法应用[J],四川大学学报(工程科学版),2008,40(1):163-166.

SHEN Jinhua,LI Yongxiang,LU Zhizheng,et al,A real-time compensation method for the geometric and thermal error on CNC turning machine[J],Journal of Sichuan University(Engineering Science Edition),2008,40(1) :163-166.

[9] 谷珂,马闯,吴洪涛,基于多体系统理论的三坐标数控铣床几何误差建模[J],机械制造与自动化,2007,36(1): 23-24.

GU Ke,MA Chuang,WU Hongtao,Modeling of positioning error for 3-axis NC milling machine tools based on multi-body system theory[J].Machine Builing and Automation,2007,36(1):23-24.

[10] WU H,ZHANG H T,GUO Q J,et al.Thermal error optimization modeling and realtime compensation on a CNC turning center[J].Journal of Materials Processing Technology,2008,207(1-3): 172-179.

[11] GUO Q J,YANG J G,WU H.Application of ACO-BPN to thermal error modeling of NC machine tool[J],International Journal of Advanced Manufacturing Technology,2010,50(5)：667-675.

[12] 张毅，杨建国,基于灰色理论预处理的神经网络机床热误差建模[J],机械工程学报,2011,47(7): 134-139.

ZHANG Yi,YANG Jianguo,Modeling for machine toolthermal error based on grey model preprocessing neuralnetwork [J],Journal of Mechanical Engineering,2011,47(7): 134-139.

[13] LEE D S，CHOI J Y，CHOI D H.ICA based thermal source extraction and thermal distortion compensation method for a machine tool[J],International Journal of Machine Tools and Manufacture,2003,43(6): 589-597.

[14] YONGJIN K，JEONG M K，OMITAOMU O A,Adaptive support vector regression analysis of closed-loop inspection accuracy[J],International Journal of Machine Tools and Manufacture,2006,46(6):603-610.

[15] SHEN S G,WANG G J,CHEN H.Support vector machine based identification of inverse dynamic model of thermal system and its application[C]//Challenges of Power Engineering and Environment,Berlin Heidelberg: Springer,2007: 914-917.

[16] 白福友,基于贝叶斯网络的数控机床热误差建模研究[D],杭州: 浙江大学,2008.

BAI Fuyou,Research on thermal error modeling of machine tools based on bayesian network[D],Hangzhou: Zhejiang University,2008.

[17] GUO Q J,YANG J G,Application of projection pursuit regression to thermal error modeling of a CNC machine tool[J],International Journal of Advanced Manufacturing Technology,2011,55(5-8): 623-629.

[18] 王海同，李铁民，王立平，等.机床热误差建模研究综述[J].机械工程学报2015(9)：119-128.

WANG Haitong,LI Tiemin,WANG Liping,et al,Rewiew on thermal error modeling of machine tools[J],Journal of Mechanical Engineering,2015(9): 119-128.

[19] 杨建国,范开国,杜正春,数控机床误差实时补偿技术[M],北京: 机械工业出版社,2013.

YANG Jianguo,FAN Kaiguo,DU Zhengchun,Technique of real-time error compensation on NC machine tools[M],Beijing:China Machine Press,2013.

[20] 张宏韬,双转台五轴数控机床误差的动态实时补偿研究[D].上海: 上海交通大学,2011.

ZHANG Hongtao,Research on dynamic and real-time error compensation for the two turntable five-axis NC machine tool[D],Shanghai:Shanghai Jiao Tong University,2011.

[21] 范开国,数控机床多误差元素综合补偿及应用 [D],上海：上海交通大学,2012.

FAN Kaiguo,Comprehencive compensation and application for multi-error elements on CNC machine[D],Shanghai: Shanghai Jiao Tong University,2012.