6-PUS并联加载机构模糊PID力控制系统设计*

樊 锐，刘力军，王 丹，郭江真

（北京航空航天大学机械工程及自动化学院，北京 100191）

樊 锐

北京航空航天大学教授，博导。主要研究方向为数控技术、传感器技术、机电控制及自动化等。1992年起参与组织International Conference on the Progress of Cutting Technology（加工技术进展国际会议），历任秘书长、副主席、主席。

可靠性是指“产品在规定条件和规定时间内完成规定功能的能力”[1]。机床可靠性试验是机床可靠性保障的基础工作。很长一段时间内，机床可靠性分析的主要信息来自于机床客户在使用过程中的数据反馈，这种方法耗时、低效，且难以控制试验条件。与之相比，试验台测试可以进行主动激发试验，效率高，条件易控制，是机床可靠性试验的重要发展方向[2]。试验台试验的关键问题是加载机构的设计，机床加工过程中主轴受力复杂，往往是多维力的共同作用，为了使试验台模拟的加工受力状况与实际加工过程相似，采用的机构需要具备输出多维力的能力。本课题研制的6-PUS并联机构，结构紧凑，刚度大，且能输出多维力，能够满足机床主轴的可靠性试验要求，适合作为加载机构对机床主轴进行加载。

6-PUS并联加载机构实现对机床主轴加载的难点在于力控制器的设计。一般情况下，控制器的设计首先要建立系统的数学模型，然而对于非线性强的系统往往很难建立其数学模型或者很难建立精确的数学模型，并且很多系统参数无法确定。对于某些系统简化的线性方程很难代表系统的实际情况[3]，浙江大学王宣银试验室研制了并联六自由度电液伺服机构，以PID控制器实现了一维力的加载[4]；哈尔滨工业大学研究了基于Steward平台的电液加载试验系统，设计了根据不同负载刚度来调整PID参数的控制策略，并仿真验证了控制方法的有效性[5]。与电液驱动不同，本文提出的6-PUS并联力加载机构采用电动驱动，控制模型复杂，且系统参数难以确定，因此适合设计非基于系统模型的控制器。模糊PID控制器既保持了传统PID的简洁性，又由于比例、积分、微分参数可以根据实际情况合理调节，可更好地适应非线性系统的特点。

本文介绍了6-PUS并联机构的多维力加载原理；建立了加载机构的数学模型，得到了表示机构末端多维力与支链力之间映射关系的力雅克比矩阵，并将对加载机构多维力的控制转化为对机构6条单支链力的控制；最后将模糊PID控制算法应用于单支链的力控制过程，并在并联机构静态情况下分别以传统PID和模糊PID对其进行了多维力静态加载试验，验证了模糊PID在6-PUS并联机构静态加载中的有效性，为后期在6-PUS并联加载机构进行动态六维力加载奠定了理论和试验基础。

加载原理介绍

1 6-PUS并联加载机构

如图1所示，6-PUS并联加载机构由静平台、动平台和6条电机驱动的支链组成。每条支链包括滚珠丝杠驱动、作为移动副的直线导轨、万向节、已知长度的连杆、可测连杆支撑力的单向力传感器和复合球铰。静平台上3个斜坡绕静平台中心轴均匀分布，移动副的直线导轨固定在斜面上，方向与斜台方向平行。此种结构可以在较小的静平台下产生尽可能大的工作空间。

图1 6-PUS并联机构实物图Fig.1 6-PUS parallel machine

动平台上设计有与被加载机构联接的接口，作为机构多维力的输出部件。在6-PUS并联机构进行静态多维力加载过程中，被加载机构始终处于静止状态，并联加载机构的动平台与被加载机构通过螺纹固定联接，当电机在移动副产生驱动力时，移动副产生一个沿力方向的运动趋势，这使得支链的连杆产生沿连杆方向的拉力或者压力，这个力可以由力传感器直接测量得到。控制卡采集6条支链力传感器数值，将6个力带入当前姿态下机构的静力学模型即可得到机构的实际多维力。同时，调节6条支链上的力就可以达到对机构输出的多维力的间接调整。以上分析可以得出：6-PUS并联机构输出的多维力是由6条支链协同配合形成，对输出多维力的控制可转化为对6条支链力的间接控制[4,6]。因此，有必要建立6-PUS并联机构的静力学力学模型，确定机构输出多维力与支链力之间相互转化的关系。

2 6-PUS力雅克比矩阵

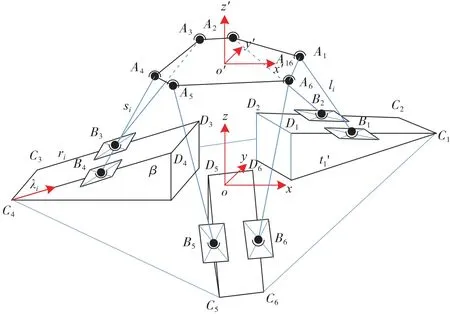
图2 6-PUS并联机构结构示意图Fig.2 Schematic diagram of 6-PUS parallel machine

如图2所示，在静平台中心位置建立世界坐标系Oxyz，在动平台中心建立动坐标系。A1，A2，…，A6和B1，B2，…，B6分别为机构支链上铰链点和下铰链在世界坐标系的位置；C1，C2，…，C6为导轨起始点在世界坐标系中的位置；λi为移动副i相对直线导轨起点Ci的位移；ri和si分别为导轨i和支链i单位方向向量。在机构工作空间内的任一位置，有以下等式成立：

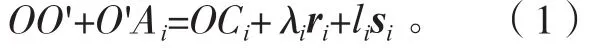
将（1）式等号两边同时对时间求导数可得：

由（2）式中各向量及其导数的物理意义，可以进一步整理为:

式中，Vm和ω分别为动平台质心在世界坐标系Oxyz中的平动速度向量和转动角速度向量；li和ωi分别为支链i的长度和其在世界坐标系Oxyz中的转动角速度；Pi代表移动副i沿导轨单位向量ri方向的速度。

将式（3）等号两边分别与si作点乘得到：

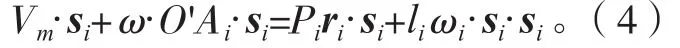
考虑到liωi·si·si=0，将式（4）移项、整理成为向量相乘的形式：

令，则可得动平台运动速度向支链驱动速度转化的关系为：

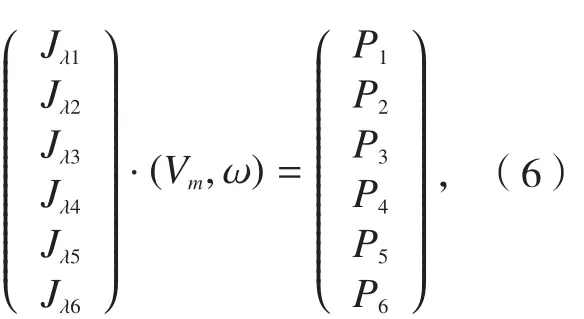
则，Jλ=（Jλ1，Jλ2，Jλ3，Jλ4，Jλ5，Jλ6）’是机构的速度雅克比矩阵。

6-PUS并联机构输出多维力为FD=（Fx，Fy，Fz，Mx，My，Mz），由相互作用力的关系可得作用在并联机构的反作用力为-FD。其中Fx，Fy，Fz分别为在世界坐标系中沿x轴、y轴、z轴的力；Mx，My，Mz分别为在世界坐标系中绕x轴、y轴、z轴的力矩。

由虚功原理可得，若使机构平衡，则作用在并联机构的作用力-FD与6个移动副驱动力的关系为[7]：

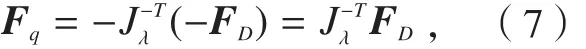
式中，Fq=（Fq1,Fq2,Fq3,Fq4,Fq5,Fq6）T为6个移动副驱动力构成的列向量。

理论上，只要控制每个支链移动副的驱动力即可，而实际6-PUS并联机构单向力传感器安装在每个支链的连杆上，并作为支链的一部分。因此，把对驱动力的控制转化成对支链的支持力的控制才能形成力闭环。如图3所示，Fqi是计算出的电机i的驱动力，Fli为支链在驱动力Fqi下的支持力，导轨与支链之间的夹角为θ。

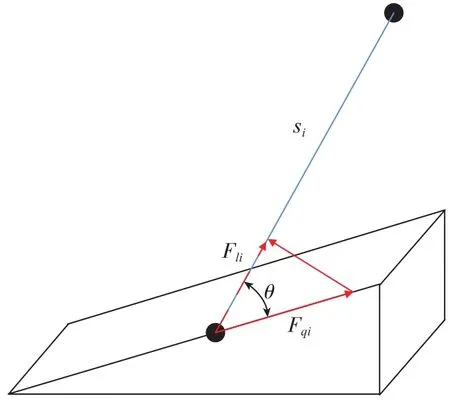
图3 支链力示意图Fig.3 Schematic diagram of limb force

则容易得到以下关系式：

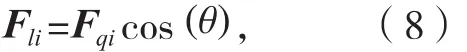
式中，cos(θ)=ri·si，即经过以上计算最终将对并联机构多维力FD的控制转化为了支链连杆支持力Fqi的间接控制。

模糊PID控制力控制

传统PID因其简洁性和易操作性，被广泛地应用于工业控制中，并且取得了良好的效果，由于其控制参数固定，在非线性控制系统中的适应性差，难以胜任系统结构变化的控制工作，因此根据控制过程不断变化的情况来实时地调节控制参数是非常必要的。模糊控制是将工程师长期的实践经验作为调节规则，通过类似人脑推理的方法得出对系统的调节规则，控制方式相比传统PID更加灵活[8]。

1 PID控制原理

PID控制器的传递函数可以表示为：

式中，U（s）是PID控制器的输出量；E（s）是期望值与实际输出值相减得到的偏差；KP是比例系数，TI是积分时间常量；TD是微分时间常量；s是拉普拉斯算子。式（9）可以进一步整理为：

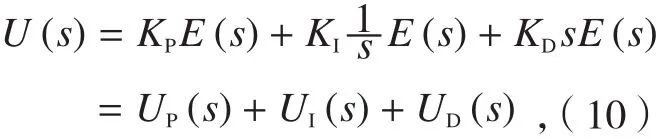
式中，KI=KP/TI是积分增益，KD=KPTD是微分增益。

将控制信号在时域内可以表示成为：

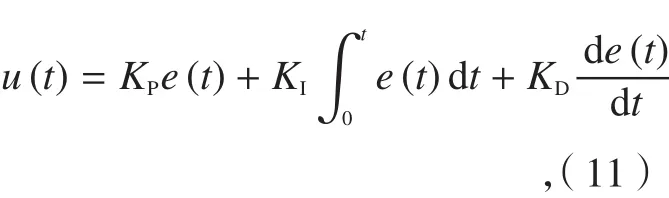
式中，e（t）是期望值与实际值的偏差，u（t）是输送给伺服电机的电压信号。

2 模糊PID控制原理

模糊PID与传统PID的区别为：模糊PID的比例、积分和微分增益是根据一定的控制规则不断变化的，模糊PID的设计任务就是设计出可以调节PID参数的控制器。模糊PID的设计可以分为以下几个步骤：

（1）量化因子选择。试验中各支链力跟随偏差的大致范围为[-60,60]，偏差变化率范围为[-600,600]。为了方便操作，将单支链力偏差e（t）及其变化率ec（t）的基本论域映射到输入语言变量论域。在实际应用中为了简化计算，满足控制的实时性要求，往往需要将输入模糊变量进行离散化处理，即将输入语言变量在论域内取有限值。将模糊语言变量e和ec的论域离散为（-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6），则实际力偏差向其对应的模糊语言变量论域映射的量化因子为Ge=6/60=0.1，偏差变化率对应的量化因子为Gec=6/600=0.01。量化因子确定后，实际偏差e（t）及偏差变化率ec（t）分别与其量化因子相乘便可得到模糊语言论域对应值e和ec，数值取舍按照四舍五入的原则[9]。

针对输入模糊语言变量e、ec和输出语言变量 ΔKP、ΔKI、ΔKD选取NB、NM、NS、ZE、PS、PM、PB7个语言变量值，其分别代表负大、负中、负小、零、正小、正中、正大。

（2）确定输入和输出语言变量。本文将单支链力目标力与单支链实际力的偏差e（t）和偏差的变化率ec（t）作为模糊控制器的输入变量，将 ΔKP，ΔKI，ΔKD作为模糊控制器的输出变量，则控制过程中模糊PID最终采用的控制参数为：

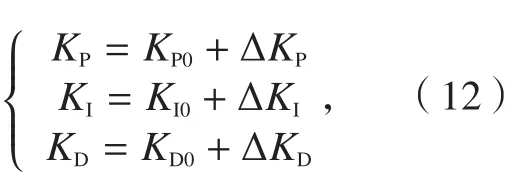
式中，KP0，KI0，KD0分别为初始比例、积分、微分系数；ΔKP，ΔKI，ΔKD分别为模糊控制器调节后的各系数增量。

将e（t）和ec（t）映射到对应的模糊论域可得e、ec。为了在输入值较小的情况下提高控制器灵敏度，e、ec的隶属度函数随着绝对值的变小逐渐变陡（图4）；输出模糊变量的隶属度函数 ΔKP，ΔKI，ΔKD在整个论域内均匀分布（图5）。

（3）模糊规则。传统PID在工业控制中使用广泛，且已经形成了比较成熟的调整原则。根据试验过程中积累的经验，可将KP、KI、KD按照表 1、2、3 的思路调整[10]。

（4）解模糊。采用重心法将输出得到的模糊集合转化为精确值[11]，并建立模糊控制离线查询表，减小在线计算的运算量，保证控制系统的实时性。

按照上面的过程可实现调整KP、KI、KD的 3 个子模糊控制器，进而构成了模糊PID的完整结构，结合对6-PUS机构单支链控制，可知单支链的模糊PID控制器结构如图6所示。其中，Fqi是单支链的期望力，Fai是单支链的实际力。

如图7所示，并联多维力加载的完整过程可以作如下总结：计算机通过光栅读取移动副的位置，代入机构正解算法得到当下机构位姿；最后根据位姿解算出机构的动力学模型，将并联机构的输出多维力FD映射到各个支链的支持力，作为各个支链上小闭环力控制的目标；力控制算法将通过控制电机丝杠滑块的微动来调节支链力，使它不断逼近期望值，进而协同输出的多维力FD。

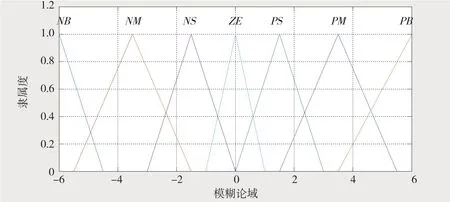
图4 e、ec隶属度函数Fig.4 Membership function for e and ec

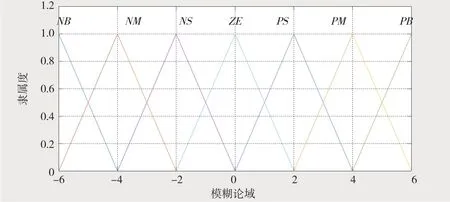
图5 ΔKP、ΔKI、ΔKD隶属度函数Fig.5 Membership fuction for ΔKP,ΔKI and ΔKD

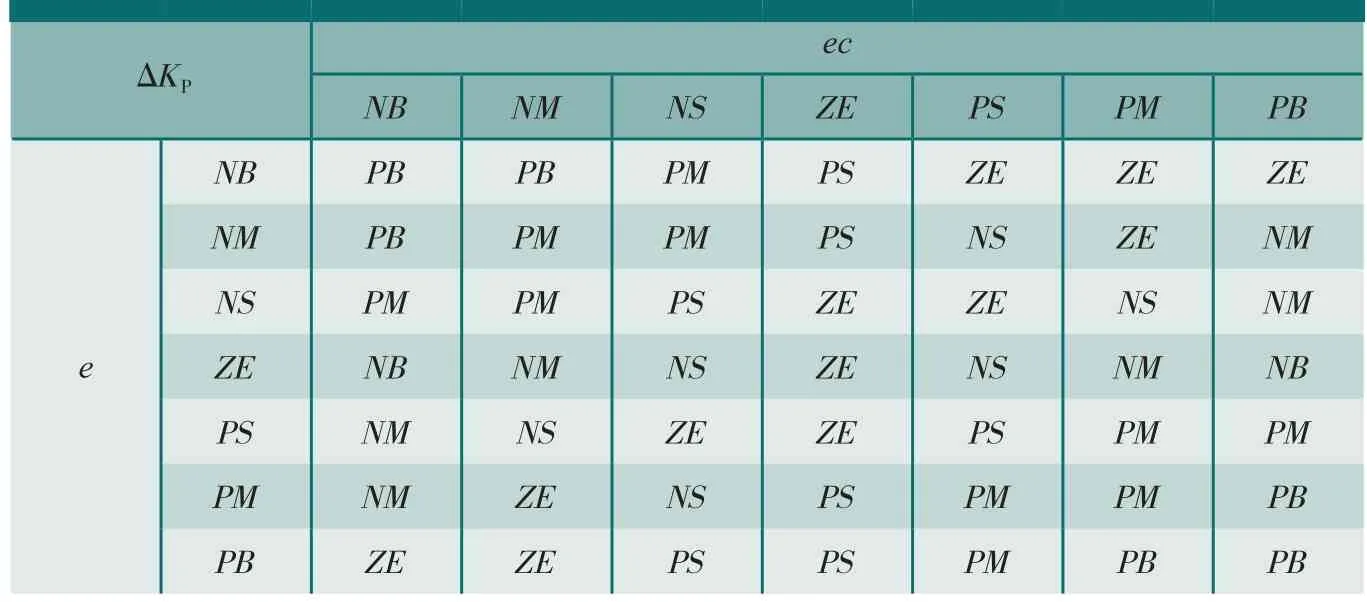
表1 ΔKP模糊规则表

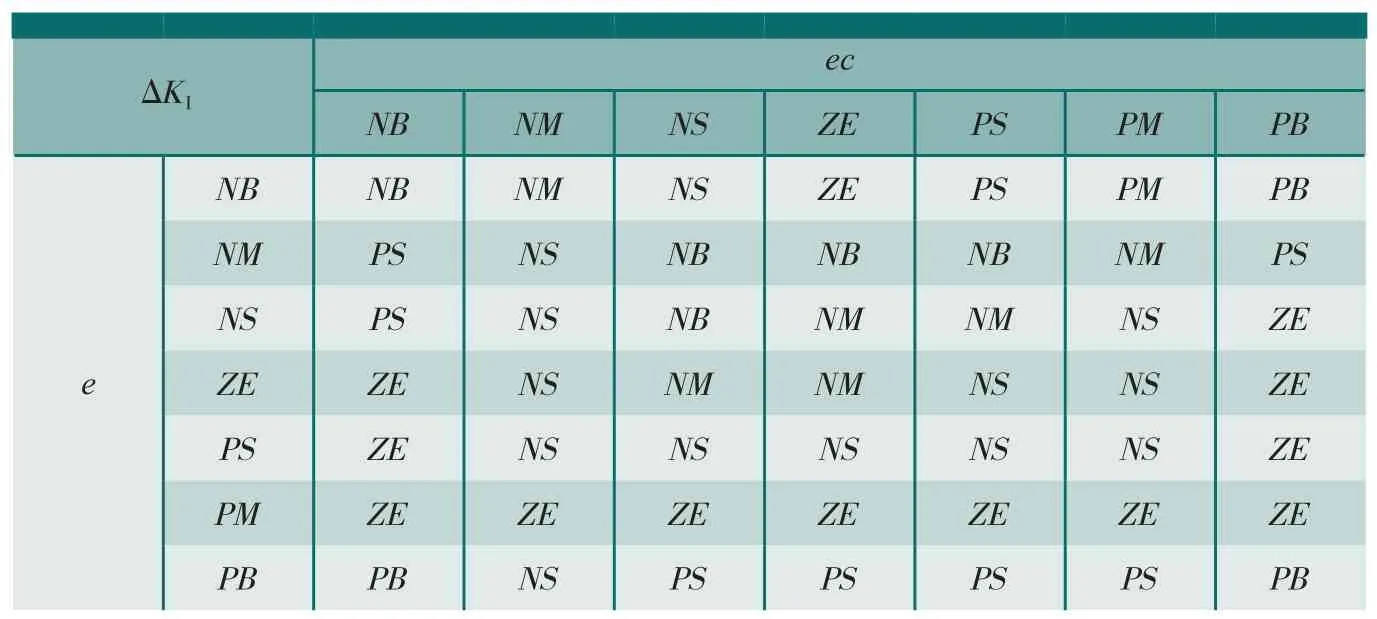
表2 ΔKI 模糊规则表

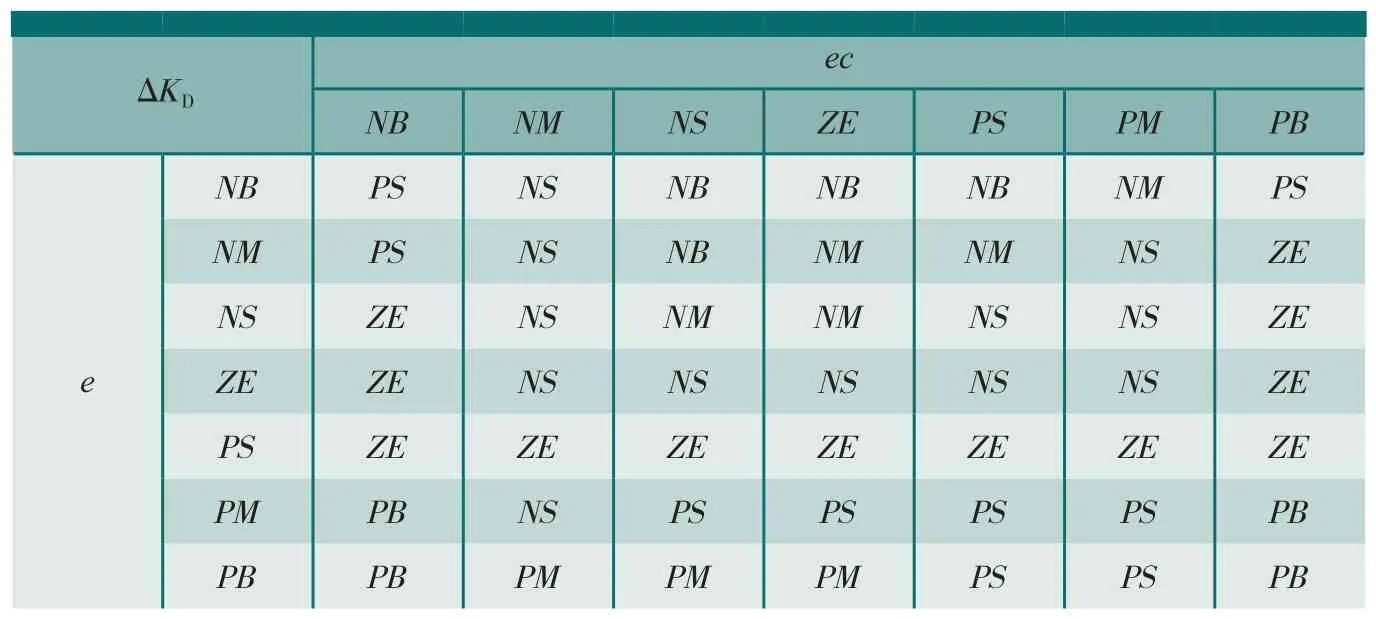
表3 ΔKD模糊规则表

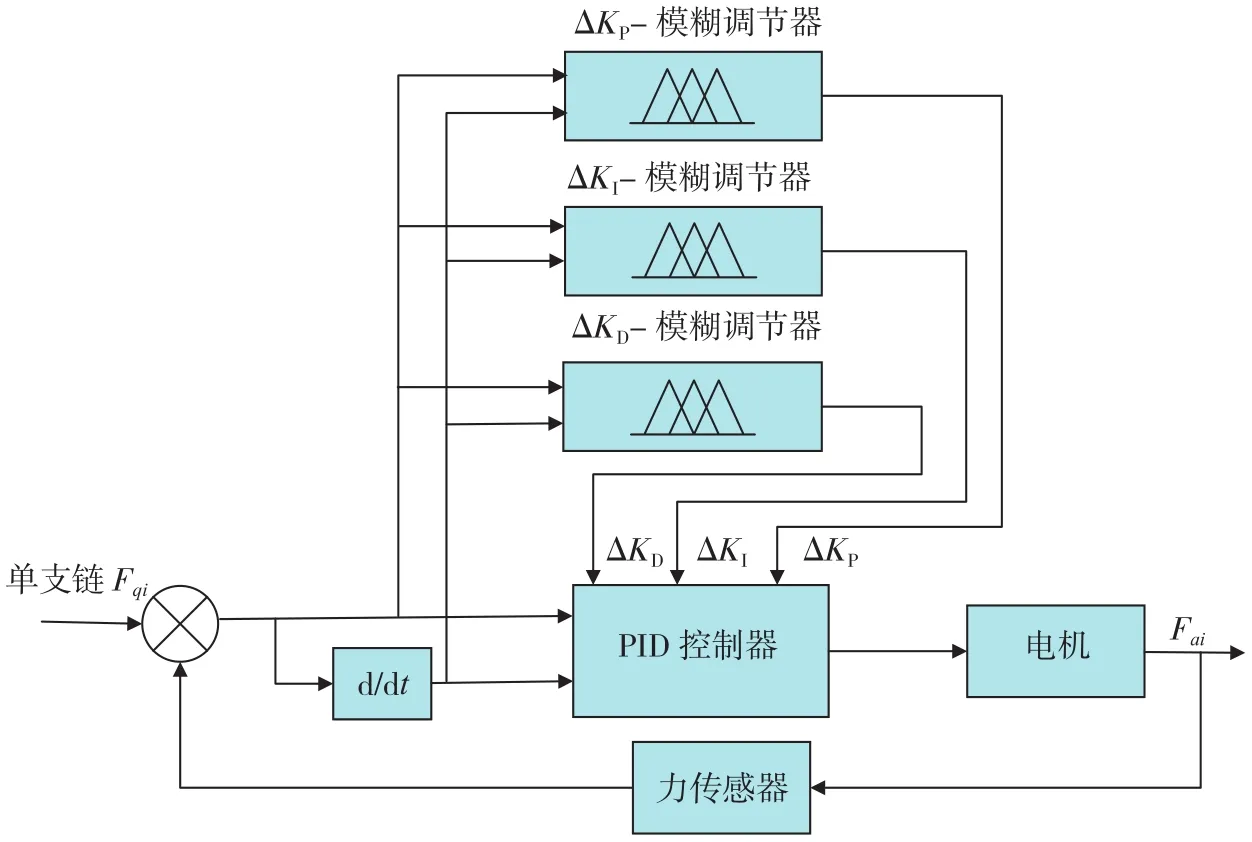
图6 单支链模糊PID控制系统图Fig.6 Configuration of fuzzy-PID controller for single limb

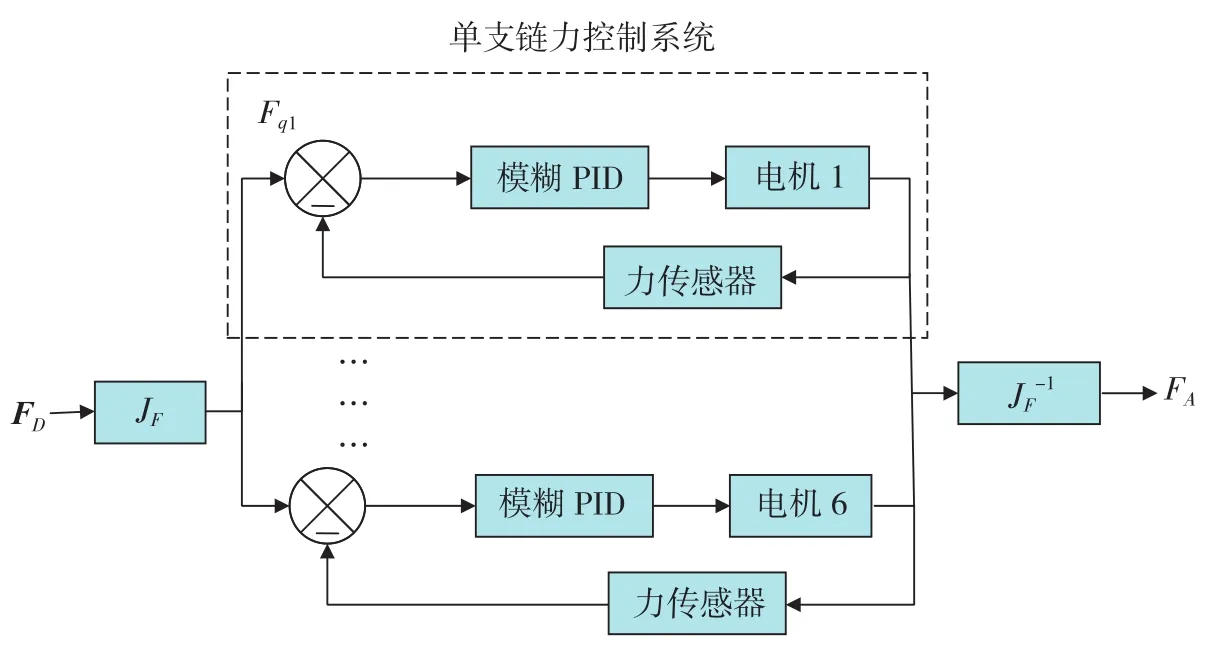
图7 模糊PID整体控制系统示意图Fig.7 Configuration of fuzzy-PID controller for whole system

加载试验

根据前文介绍的试验原理搭建了多维力加载平台，如图8所示。龙门结构作为加载试验中的被加载对象，固定在基座上；6-PUS并联机构静平台固定在底座上，动平台与龙门通过专门设计的接口卡紧；加载机构的输出力是通过支链力来合成得到的，因此加载机构既充当了加载部件的角色，同时还承担了测量多维力的任务。

图8 加载试验台实物图Fig.8 Load test bench

试验系统的驱动元件采用日本安川SGDM-08ADA型交流伺服电机，控制器为美国泰道公司Power PMAC运动控制卡，支链的传感器为BK-2B S型测力传感器。试验时，6-PUS动平台的质心位置为世界坐标系正上方450mm处；在控制过程中，电机需要通过微小的转动变化来调节支链力的大小，控制卡需要实时的计算并更新加载机构的位姿，因此，实际上并联加载机构在世界坐标系正上方450mm处附近微动。

为了检验本文采用的模糊PID控制器在实际应用中的效果，在相同的试验环境及机构姿态点的情况下分别采用传统PID及模糊PID进行了六维力阶跃信号响应试验，将信号写为六维力的形式FD=（200,200,200,10,10,10）T。值得注意的是，此六维力的加载是同时向x、y和z轴施加力和力矩，为了将每个单维度的力表达得更清晰，下面将6个力的响应曲线单独绘制。

x向200N阶跃力信号响应如图9所示，可以看出模糊PID控制器超调量约为25N，远小于传统PID的约75N的超调量；模糊PID控制器上升时间略快于传统PID，更快地趋于稳定。

图9 x 向力响应曲线Fig.9 Force response of x axis

y向200N阶跃力响应曲线如图10所示，可以看出在y向200N阶跃响应中，模糊PID的超调量约为50N，明显小于传统PID约为90N的超调量；模糊PID控制器上升时间略快于传统PID系统，且更快地趋于稳定。

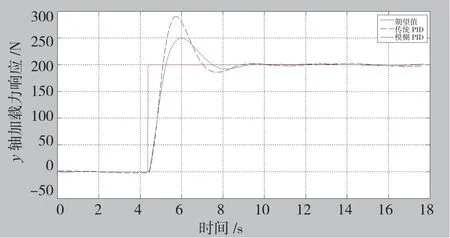
图10 y 向力响应曲线Fig.10 Force response of y axis

z向200N阶跃力响应曲线如图11所示，可以看出在z向200N阶跃响应中，模糊PID的超调量约为25N，明显小于传统PID约为75N的超调量；模糊PID控制器上升时间略快于传统PID系统，且更快地趋于稳定。

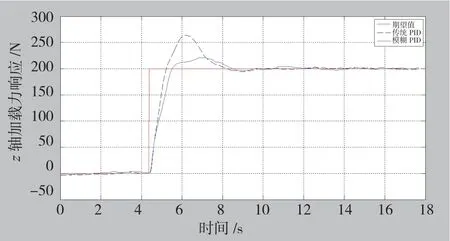
图11 z 向力响应曲线Fig.11 Force response of z axis

x、y、z轴的力矩如图12、图13、图14所示，可以看出当对机构输入幅值为10Nm的阶跃力矩信号时，模糊PID控制器响应过程中的超调量明显小与传统PID控制器造成的超调量。从图9x向力加载曲线和图13y轴力矩加载响应速度较慢可以推断，龙门x向刚度较其他两个方向较弱，这一点可以从龙门的结构得到验证，如图8中x向缺少挡板，刚度较弱，因此加载力响应特性比其他两个方向差。

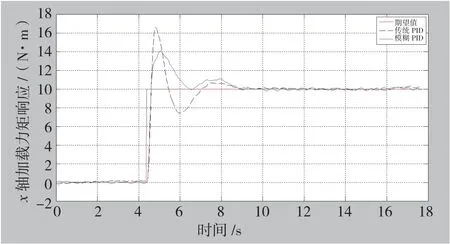
图12 x 轴力矩响应曲线Fig.12 Torch response of x axis

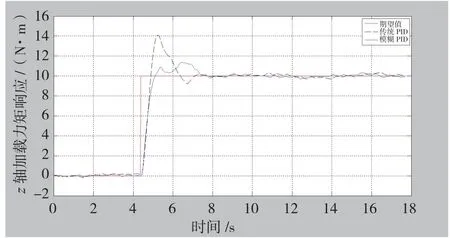
图14 z 轴力矩响应曲线Fig.14 Torch response of z axis

结论

以上分析可知，在6-PUS并联多维力加载机构中，模糊PID控制器由于在响应过程中不断调整控制参数，适应了不同阶段对控制器参数变化的要求，整体上动态响应性能更优于传统PID控制器，表明了模糊PID控制器在6-PUS并联力加载机构力控制上的有效性，为后期进行多维力的动态加载奠定了基础。

[1] 可靠性基本名词术语及定义:GB3187-82 [S],北京: 国家质检总局,1982.

Basic terms and definitions of reliability:GB3187-82 [S],Beijing: General Administration of Quality Supervision,Inspection and Quarantine of the People’s Republic of China,1982.

[2] 杨兆军,陈传海,陈菲,等, 数控机床可靠性技术的研究进展[J],机械工程学报,2013,49(20): 130-139.

YANG Zhaojun,CHEN Chuanhai,CHEN Fei,et al,Progress in the research of reliability technology of machine tools[J],Journal of Mechanical Engineering,2013,49(20):130-139.

[3] LIU R,WANG X Y,HUANG X C,Hybrid fuzzy PID control of hydraulic robot[C],2002 ASME International Mechanical Engineering Congress & Exposition,2002: 935-938.

[4] 王宣银,吴剑,吴乐彬, 基于并联六自由度电液伺服机构的力控制方法[J],上海交通大学学报,2007,41(1): 111-115.

WANG Xuanyin,WU Jian,WU Lebin,The force control method based on 6 DOF parallel electro hydraulic servo mechanism[J],Journal of Shanghai Jiaotong University,2007,41(1): 111-115.

[5] 徐彬,基于并联机构的多维力加载实验系统研究[D],哈尔滨: 哈尔滨工业大学,2013: 53-68.

XU Bin,Research on the multi-DOF loading system based on parallel machanism[D].Harbin: Harbin Institute of Technology,2013:53-68.

[6] 吴剑,基于并联六自由度电液伺服机构的单自由度力控制研究[D],杭州: 浙江大学,2006: 20-28.

WU Jian,Research of single-DOF force control based on 6-DOF parallel electrohydraulic servo mechanism[D],Hangzhou:Zhejiang University,2006: 20-28.

[7] TSAI L W,Solving the inverse dynamics of a stewart-gough manipulator by the principle of virtual work[J],Journal of Mechanical Design,2000,122(1): 3-9.

[8] TRUONG D Q,AHN K K,SOO K J.Application of fuzzy-PID controller in hydraulic load simulator[C],2007 International Conference on Mechatronics and Automation (ICMA 2007),Harbin,2007: 3338-3343.

[9] 韩力群,智能控制理论及应用[M].北京: 机械工业出版社,2007: 15-95.

HAN Liqun,Intelligent control theory and applications[M],Beijing: China Machine Press,2007: 15-95.

[10] 丁坚,模糊PID控制器的研究[D].哈尔滨: 哈尔滨工程大学,2009: 19-60.

DING Jian,Research on fuzzy PID controller[D],Harbin: Harbin Engineering University,2009: 19-60.

[11] PASSINO K M,YURKOVICH S.Fuzzy Control[M],London: Addison Wesley Longman,1998.