基于局部相关性的kNN分类算法

邓振云，龚永红，2，孙　可，张继连

(1.广西师范大学广西多源信息挖掘与安全重点实验室，广西桂林541004；2.桂林航天工业学院，广西桂林541004)



基于局部相关性的kNN分类算法

邓振云1，龚永红1，2，孙可1，张继连1

(1.广西师范大学广西多源信息挖掘与安全重点实验室，广西桂林541004；2.桂林航天工业学院，广西桂林541004)

摘要：kNN算法作为一种简单、有效的分类算法，在文本分类中得到广泛的应用。但是在k值(通常是固定的)的选取问题上通常是人为设定。为此，本文引入了重构和局部保持投影(locality preserving projections，LPP)技术用于最近邻分类，使得k值的选取是由样本间的相关性和拓扑结构决定。该算法利用l1-范数稀疏编码方法使每个测试样本都由它的k(不固定)个最近邻样本来重构，同时通过LPP保持重构前后样本间的局部结构不变，不仅解决了k值的选取问题，并且避免了固定k值对分类的影响。实验结果表明，该方法的分类性能优于经典kNN算法。

关键词：kNN；保局投影；重构；稀疏编码

0引言

在数据挖掘的研究与应用中，分类是用于预测分析的重要方式之一。它是一种有监督的学习，通过对训练样本的分析，从中归纳出分类规则，以此来预测测试样本的类别。目前常见的分类算法主要有：决策树、关联规则、贝叶斯、神经网络、遗传算法、kNN算法等。本文集中在kNN分类算法的研究。

由于kNN算法在样本较大以及特征属性较多时，分类的效率就将大大降低，因此近年来学者们提出了许多针对kNN的改进算法。如文献[1]提出将粗糙集理论应用到kNN算法中，实现属性约简，解决了kNN算法分类效率低的缺点；文献[2]提出一种基于密度的样本裁剪方法，降低kNN的计算量，提高分类的性能；文献[3]提出一种基于类别的kNN改进模型，解决k近邻选择时大类别、高密度样本占优问题等；文献[4]提出一种充分利用已知类别标签数据进行自训练的半监督分类算法，显著地提高了分类的准确率。这些算法主要通过一定的优化策略或降维方法减少样本之间相关性的计算，以提高分类的效率。而本文直接考虑样本间的相关性、样本的拓扑结构，对于kNN算法中k值的选取直接由数据本身驱动，避免了人为设定k值对分类的影响。

kNN算法是一种基于实例的学习方法[5]，最初用于解决文本分类的问题。其基本思想是：在训练样本中找到待测样本的k(定值)[6-7]个最近邻样本，然后根据这k个最近邻样本的类别进行投票，以此来决定测试样本的类别。但是在实际应用中，这种采取固定k值的方法经常是不合理的，如图1。

当k=5时，根据kNN分类算法将得到两个样本空间(图1中两个实线圆圈)。其中待测样本1的k个最近邻样本选取合理，但对于待测样本2而言，实际上令k=3更为合理(如虚线圆圈所示)，因为下方两个训练样本距离待测样本2较远，如果把它们也作为最近邻样本，很可能会影响分类准确率。因此本文也认为：对于测试样本取相同的k值是不合理的[8]；k值的选取应该由数据的分布或特点决定，即k值是从数据中学习的，对不同的测试样本它的取值应该是不固定的。为了更加准确地根据数据分布或特点学习k值，应当充分考虑数据中的先验知识，例如样本间的相关性、样本的拓扑结构等。

根据以上理论，本文用训练样本重构所有测试样本生成相关性矩阵，并通过l1-范数稀疏编码方法[9-11]对矩阵进行重构[12]，使得每个测试样本都由它的k个相关的最近邻样本预测，同时通过LPP保持了样本的局部结构而不受重构影响。这样便使得每个测试样本都由它的k(不固定)个相关的最近邻样本预测，分类的性能得到很大的提高。本文将提出的算法简称为LS-kNN(LPP-Sparse-kNN)算法。

1LS-kNN算法

1.1局部保持投影(LPP)

LPP是非线性方法拉普拉斯特征映射(Laplacian eigenmap)的线性近似，其特点是获得原始数据在低维度上的投影，且保持数据的非线性流形特征不变。LPP算法的基础是构造一个模拟局部结构的最近邻图，本算法应用此特性即构造一个模拟测试样本的最近邻的矩阵W。通常采用最小化目标函数式(1)来确定这个最近邻矩阵W：

(1)

对公式(1)进行代数变化操作后发现，特征空间保持了原始的局部结构。操作如下：

tr(WTXDXTW)-tr(WTXSXTW)=tr(WTXLXTW)。

(2)

1.2重构

假设训练集X∈Rn×d，测试集Y∈Rm×d，其中m、n、d分别是测试样本的个数、训练样本个数和样本的维数。本文算法的核心是通过训练样本去重构测试样本，得到一个相关性矩阵W∈Rn×m，使得Y与WTX尽可能差距最少。这可以通过最小二乘损失函数[13]实现，即：

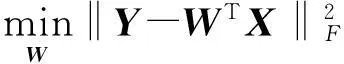
(3)

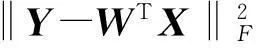
1.3LS-kNN算法的描述

由于公式(3)是凸函数，易知其解为W*=(XTX)-1XTY。但XTX在实际应用中不一定可逆，对此通常会考虑岭回归从而引入一个l2-范数使得函数可逆：

(4)

(5)

通过目标函数(5)进行重构将得到如下形式的投影矩阵W：

根据重构技术可知wij≠0即为相关的样本，且第j列中wij≠0的个数即为第j个测试样本最近邻样本的个数。因此从矩阵W的形式可判断，第一个测试样本(第一列)的最近邻样本数为2，即k=2，第二个测试样本的最近邻数为4。以此类推，可发现测试样本没有采用固定的最近邻数即没有用固定k值去寻找训练样本。

综上可知，LS-kNN算法通过考虑样本间的相关性，有效地解决了kNN分类存在的问题，并通过LPP保证了数据内部分布的完整性。注意，l2-范数就无法实现这个功能，因为它得到的矩阵不稀疏。

最后，给出LS-kNN分类算法的具体步骤。

算法1：LS-kNN分类算法。

输入：样本集，并作规范化处理。

输出：测试集的类标签。

1：由ADMM优化算法(6)得到最优解W；

2：根据W找到每个测试样本对应的k个最近邻训练样本；

3：对每个测试样本，用与其对应的k个最近邻样本的类标签进行分类投票；

4：输出测试样本的类标签。

2LS-kNN算法的优化

由于目标函数(5)是凸且非平滑的，因此本文采用ADMM(alternating direction method of multipliers)[15]算法来优化此函数。目标函数(5)可等效于求解以下N个独立的子问题：

(6)

其中wi向量是W的第i个列子向量且vec(W)=[w1，w2，…，wn]T。对目标函数(6)进行ADMM优化，在目标函数(5)上增加一个虚拟变量(dummy variable)C使函数转换为：

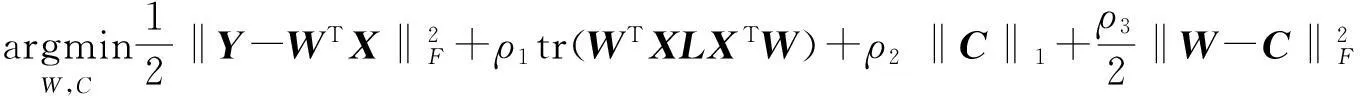
(7)

公式(7)较为复杂，因此可以使用扩展拉格朗日进行替代，使其变成如下形式：

(8)

ADMM算法采用迭代法思想，包括如下的迭代步骤：

(9)

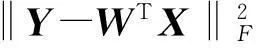
通过以上分析，本文将目标函数(5)拆分为N个独立的子问题，再使用ADMM算法求解最优化的W。

算法2： ADMM算法，W的优化。

Input： 数据集、惩罚函数ρ3。

Output：W、Λ。

1： InitializeW0，C0，Λ0；

2： repeat

3：Wk+1←Wk；

4：Ck+1←Ck；

5：Λk+1←Λk+ρ3(W+C)；

6：k=k+1；

7：UntilW最优。

3实验与结果分析

为了验证算法的有效性，本文以分类准确率作为评价指标。用kNN分类算法、LMNN算法以及本文的LS-kNN改进算法，在LIBSVM数据集[16]上选取4个数据集ionosophere、seeds、heart、cheveland进行实验(为了使数据特征之间具有可比性，已对数据集进行了标准化处理)。

为了保证3个算法比较的公平性，本实验对样本事先采取相同的预处理，并在每个数据集上用十折交叉验证法做10次实验来看算法效果。对于kNN和LMNN算法，我们令k=5；而LS-kNN算法的k值是由数据驱动产生，无需事先处理。最后对3种算法得到的实验结果进行比较。

实验结果的优劣由分类准确率评定。多次实验得到的分类准确率结果可以反映分类的可信度以及算法的稳定性。分类准确率的均值越高，可信度也就越高，稳定性越强。分类准确率的计算公式如下：

(11)

其中nmatch为测试样本中正确分类的个数，n为测试样本的总数。

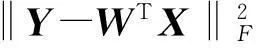
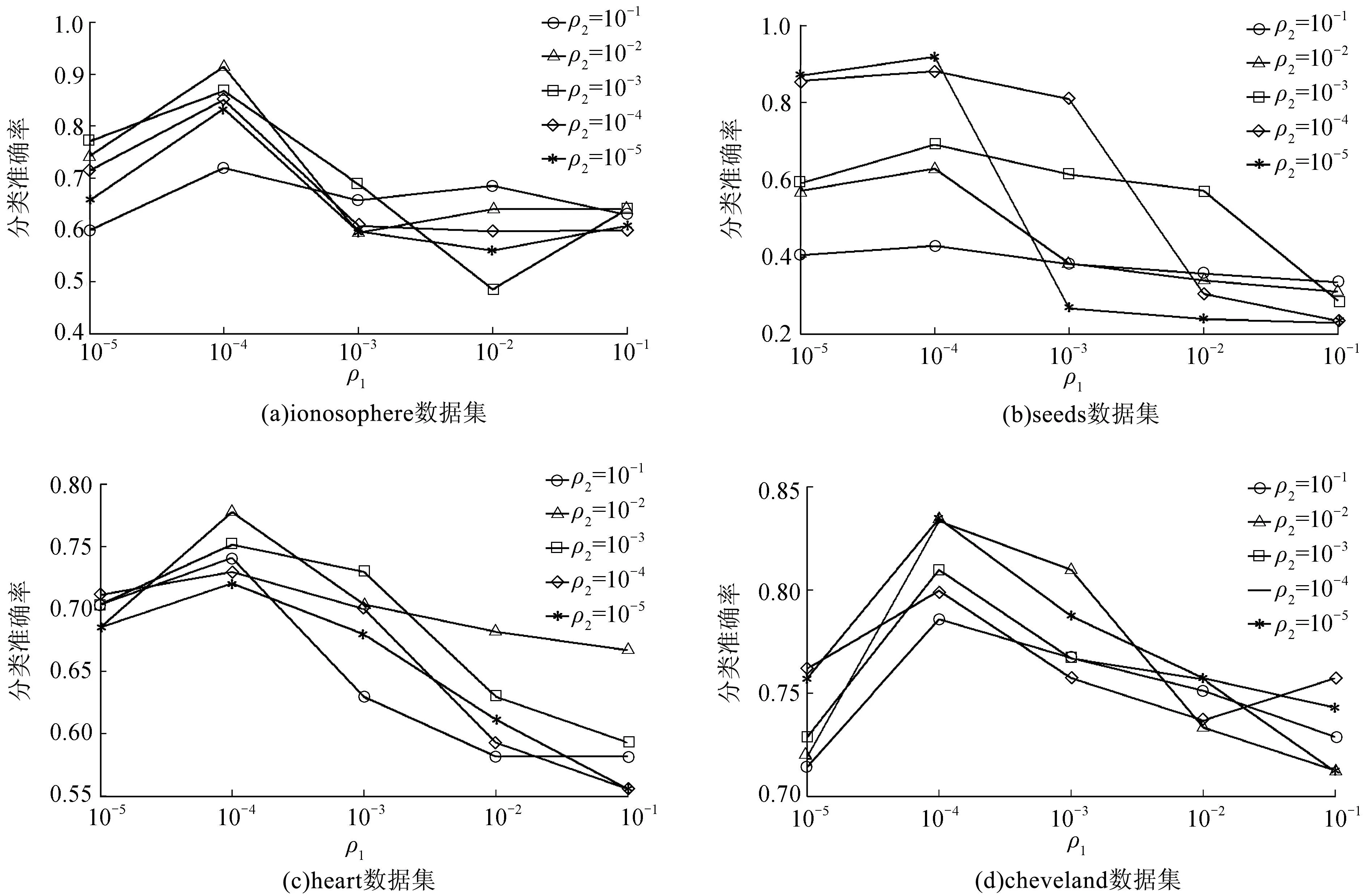
图2　LS-kNN算法在不同数据集不同参数取值下的分类准确率Fig.2　Classification accuracy of LS-kNN on the different datasets with different parameter setting

从图2可以看出，当参数ρ1∈(10-5，10-4)，ρ2∈(10-5，10-4)范围时，LS-kNN算法的分类准确率达到最优，因此我们将在后面的对比实验中，令ρ1、ρ2在(10-5，10-4)范围内随机取值。

通过对ρ1、ρ2进行调参使LS-kNN达到最优，我们将其与kNN算法和LMNN算法进行对比，实验过程中对每个数据集都重复10次，不但报告每次的实验结果而且报告10次结果的均值和方差，如表1。

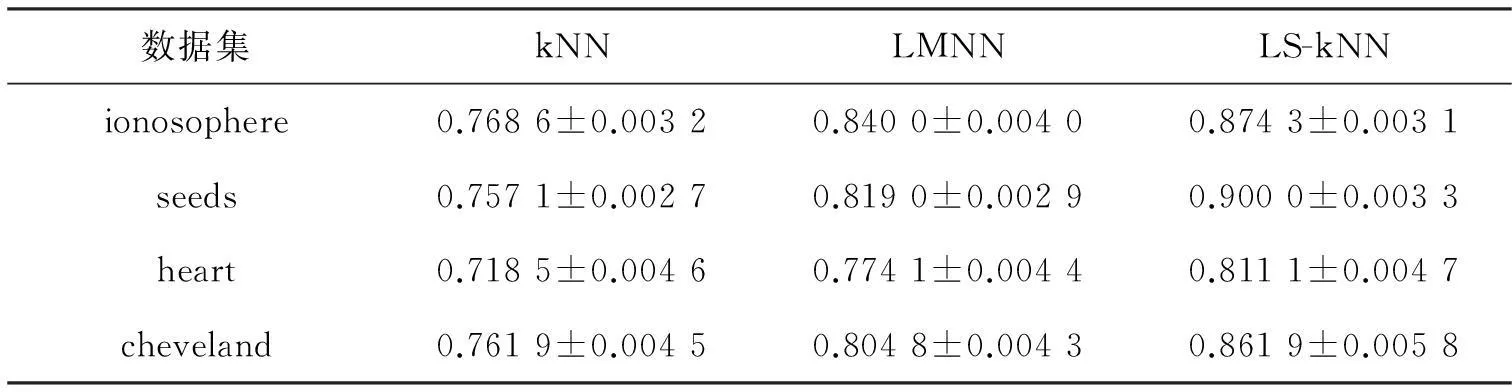
表1　kNN、LMNN与LS-kNN算法的分类准确率

为了更加直观地比较kNN、LMNN和LS-kNN的分类性能，我们做了对比图，如图3所示。由图3中4个数据集得出的实验结果可知，LS-kNN算法的分类准确率明显高于传统kNN和LMNN算法。

图3　kNN，LMNN与LS-kNN算法在4个数据集上的分类准确率Fig.3　Classification accuracy of kNN，LMNN and LS-kNN on four datasets

4结束语

本文提出了一种基于LPP和l1-范数的kNN改进算法LS-kNN，有效解决了传统kNN分类算法中的两个缺陷：k值需事先给定且固定；未考虑样本之间的相关性。该算法思想是根据样本的相关性和拓扑结构，用训练样本对所有测试样本进行重构，以实现k值的选取由数据本身驱动，而无需人为设定。因此，本算法可用于无法通过经验或者需要长时间实验选定k值的情况，大幅度减少选取k值的时间。最后通过与两种算法以分类准确率为评价标准进行对比实验，实验结果表明，LS-kNN算法的分类准确率优于kNN分类算法。

参考文献：

[1]张著英，黄玉龙，王翰虎. 一个高效的KNN分类算法[J]. 计算机科学，2008，35(3)：170-172.

[2]李荣陆，胡运发. 基于密度的kNN文本分类器训练样本裁剪方法[J]. 计算机研究与发展，2004，41(4)：539-545.

[3]张孝飞，黄河燕. 一种采用聚类技术改进的KNN文本分类方法[J]. 模式识别与人工智能，2009，22(6)：936-940.

[4]陆广泉，谢扬才，刘星，等. 一种基于KNN的半监督分类改进算法[J]. 广西师范大学学报(自然科学版)，2012，30(1)：45-49. DOI: 10.16088/j.issn.1001-6600.2012.01.004.

[5]HAN Jiawei，KAMBER M. Data mining： concepts and techniques[M]. Waltham, MA: Morgan Kanfmann Publishers，2000.

[6]ZHANG Shichao.Cost-sensitive classification with respect to waiting cost[J]. Knowledge-Based Systems, 2010，23(5)： 369-378. DOI: 10.1016/j.knosys.2010.01.008.

[7]LALL U，SHARMA A.A nearest neighbor bootstrap for resampling hydrologic time series[J].Water Resouarces Research，1996，32(3)： 679-693. DOI: 10.1029/95WR02966.

[8]LIU Huawen，ZHANG Shichao.Noisy data elimination using mutualk-nearest neighbor for classification mining[J]. Journal of Systems and Software，2012，85(5)： 1067-1074. DOI:10.1016/j.jss.2011.12.019.

[9]WU Xindong，ZHANG Chengqi，ZHANG Shichao.Database classification for multi-database mining[J]. Information Systems, 2005，30(1)： 71-88. DOI:10.1016/j.is.2003.10.001.

[10]JENATTON R，GRAMFORT A，MICHEL V，et al. Multi-scale mining of fMRI data with hierarchical structured sparsity[J]. Siam Journal on Imaging Sciences，2012，5(3)： 835-856. DOI:10.1137/110832380.

[11]ZHU Xiaofeng，HUANG Zi，SHEN Hengtao，et al. Dimentionality reduction by mixed-kernel canonical correlation analysis[J]. Pattern Recognition，2012，45(8)： 3003-3016. DOI:10.1016/j.patcog.2012.02.007.

[12]ZHU Xiaofeng，HUANG Zi，CHENG Hong，et al.Sparse hashing for fast for fast multimedia search[J]. ACM Transaction on Information System，2013，31(2)： 9. DOI:10.1145/2457465.2457469.

[13]KANG P，CHO S. Locally linear reconstruction for instance-based learning[J]. Pattern Recogntion，2008，41(11)： 3507-3518. DOI: 10.1016/j.patcog. 2008.04.009.

[14]LIANG Jinjin，WU De.Sparse least square support vector machine with L1 norm[J]. Computer Engineering and Design，2014，35(1)： 293-296，338.

[15]BOYD S. Alternating direction method of multipliers[EB/OL]. [2015-03-25]. http://stanford.edu/class/ee364b/lectures/admm_slides.pdf.

[16]CHANG C C，LIN C J.LIBSVM： A library for support vector machine[J]. ACM Transactions on Intelligent Systems and Technology，2011，2(3)：27.DOI： 10.1145/1961189.1961199.

(责任编辑黄勇)

A kNN Classification Algorithm Based on Local Correlation

DENG Zhenyun1，GONG Yonghong1，2，SUN Ke1，ZHANG Jilian1

(1. Guangxi Key Lab of Multi-source Information Mining & Security，Guangxi Normal University，Guilin Guangxi 541004，China； 2. Guilin University of Aerospace Technology，Guilin Guangxi 541004，China)

Abstract:As a simple and effective classification algorithm, kNN algorithm is widely used in text classification. However, the k value (usually fixed) is usually set by users. For this purpose, the reconstruction and locality preserving projections (LPP) technology is introduced into the nearest neighbor classification, which makes the selection of the k value to be determined by the correlation between the samples and the topology structure. The algorithm uses l1-norm sparse coding method to reconstruct the test sample by its k (not fixed) nearest neighbor samples and LPP keeps the local structure of the sample after the reconstruction, which not only solves the problem of choosing k value, but also avoids the influence of fixed k value on classification. Experimental results show that the classification performance of the proposed method is better than that of the classical kNN algorithm.

Keywords:k-nearest neighbor； locality preserving projections； reconstruction； sparse coding

中图分类号：TP181

文献标志码：A

文章编号：1001-6600(2016)01-0052-07

基金项目：国家自然科学基金资助项目(61573270,61263035，61363009)；国家973计划项目(2013CB329404)；广西自然科学基金资助项目(2012GXNSFGA060004,2015GXNSFCB139011)；中国博士后科学基金资助项目(2015M570837)；广西多源信息挖掘与安全重点实验室开放基金资助项目(MIMS13-08)

收稿日期：2015-06-16

doi:10.16088/j.issn.1001-6600.2016.01.008

通信联系人：张继连(1977—)，男，广西桂林人，广西师范大学教授，博士。E-mail:jiliangzhang@sina.com；龚永红(1970—)，女，广西永福人，桂林航天工业学院副教授。E-mail: zysjd2015@163.com