群环ZnG的理想化零因子图的性质

郭述锋，谢光明，易　忠，3

(1.首都师范大学数学科学学院，北京100048；2.广西师范大学数学与统计学院，广西桂林541004；3.桂林航天工业学院，广西桂林541004)



群环ZnG的理想化零因子图的性质

郭述锋1，2，谢光明2，易忠2，3

(1.首都师范大学数学科学学院，北京100048；2.广西师范大学数学与统计学院，广西桂林541004；3.桂林航天工业学院，广西桂林541004)

摘要：研究环的零因子图，以图的方式清晰、直观地刻画环的零因子的结构，这对理解环的结构本身具有重要意义。本文主要讨论了群环ZnG关于增广理想Δ(G)的理想化ZnG(+)Δ(G)的零因子图的性质，分别给出了环ZnG(+)Δ(G)的零因子图的围长、直径和平面性的详细刻画，其中G为素数阶群。

关键词：群环； 零因子图； 围长； 直径；平面性

0引言

设R是有单位元的交换环。R的零因子图是指一个简单图Γ(R)，它的顶点集为R的非零零因子组成的集合D(R)*，两个不同的顶点x与y有一条边连接⟺xy=0。1999年，Anderson和Livingston在文献[1]中首次给出了上述定义，并且获得了交换环R的零因子图Γ(R)的一些基本结果：对任意的交换环R，R的零因子图Γ(R)是连通的，Γ(R)的围长只能为3、4、∞，Γ(R)的直径只能为0、1、2、3。此后，零因子图的研究开始成为代数学研究的一个热点领域，产生了一系列丰富的成果[2-10]。

研究代数系统的零因子图，对于理解代数系统结构本身是很有意义的，这种研究方法的重要性在于其将代数系统的零因子的结构以图的形式给出一个比较清晰的描述，这种方法特别适用于仅含有有限个元素的代数系统的研究。2006年，Axtel和Stickles在文献[2]中研究了交换环R关于R-模M的平凡扩张的零因子图的性质，对此平凡扩张的零因子图的围长、直径等问题做了一些讨论，得到了一些深刻的结果。在文献[10]中，我们讨论了群环ZnG的零因子图的性质，具体描述了ZnG的零因子图的围长、直径和平面性，其中G为素数阶群。在本文中，我们将继续研究与群环ZnG密切相关的一类环，以ZnG(+)Δ(G)表示，称之为ZnG关于Δ(G)的理想化。我们主要研究环ZnG(+)Δ(G)的零因子图Γ(ZnG(+)Δ(G))的性质，分别给出Γ(ZnG(+)Δ(G))的围长、平面性和直径的较为具体的刻画。

本文中的群环ZnG，Zn均为模n剩余类环(n>1)，G均为素数p阶群。记Zn={0，1，2，…，n-1}，G={1，a，a2，…，ap-1}，其中a的阶∘(a)=p。群环ZnG关于增广理想Δ(G)的理想化是指集合{(α，x)|α∈ZnG，x∈Δ(G)}按照以下两种运算做成的环：

(ⅰ)(α，x)+(β，y)=(α+β，x+y)；

(ⅱ)(α，x)(β，y)=(αβ，αy+βx+xy)。

将其记作ZnG(+)Δ(G)。易证ZnG(+)Δ(G)是有单位元(1，0)的交换环。

下面，我们主要陈述一些有关图的基本概念和符号。设Γ是一个图，将Γ中最短圈的长度称为Γ的围长，记作gr(Γ)，如果Γ中不含圈，则称gr(Γ)=∞；设x和y是Γ的两个顶点，将x与y之间的所有路径中最短路的长度称为x与y之间的距离，记为d(x，y)，Γ的直径定义为diam(Γ)=sup{d(x，y)|x，y∈V(Γ)}；如果Γ能画在平面上使得它的边仅在端点处相交，则称Γ为平面图；如果Γ中任意两个顶点之间都有一条路相连，则称Γ为连通图；如果Γ中任意两点均有单边相连，则称Γ为完全图，以Kn表示。我们将完全二部图表示为Km，n。设A是环R的子集，我们用|A|表示A的元素个数，A*=A-{0}。关于群环的基本性质参见文献[11-12]，关于图的有关其他概念和符号参见文献[13]。

1环ZnG(+)Δ(G)的零因子

本节将得到环ZnG(+)Δ(G)的所有零因子。以下引理是文献[3]命题2.2的一个直接的结果：

引理1设ZnG为群环，Δ(G)为ZnG的增广理想，其中G为素数阶循环群。则环ZnG(+)Δ(G)的零因子集合D(ZnG(+)Δ(G))={(0，x)|x∈Δ(G)}∪{(x，-x)|x∈Δ(G)} ∪ {(α，x)|α∈D(ZnG)*，x∈Δ(G)}∪{(α，x)|α∈ZnGD(ZnG)，x∈Δ(G)，∃y∈Δ(G)*，使得y(α+x)=0}。

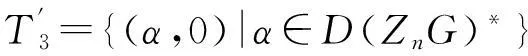
2Γ(ZnG(+)Δ(G))的围长与平面性

在本节中，我们主要研究Γ(ZnG(+)Δ(G))的围长与平面性。首先，我们给出Γ(ZnG(+)Δ(G))的围长的一个刻画：

定理1设Zn为模n剩余类环，G为素数p阶群，Δ(G)为群环ZnG的增广理想，则gr(Γ(ZnG(+)Δ(G)))=3。

证明由于在Γ(ZnG(+)Δ(G))中，(0，a-1)—(1+a+…+ap-1，0)—(a-1，1-a)—(0，a-1)构成了一个长为3的圈，故gr(Γ(ZnG(+)Δ(G)))=3。证毕。

其次，我们研究Γ(ZnG(+)Δ(G))的平面性。在证明主要结果时，我们需要以下引理。

引理2(文献[13]定理9.5)图Γ是平面图的充分必要条件是K5或K3，3的任何细分都不是Γ的子图。

引理3(文献[10]定理3)设Zn为模n剩余类环，G为素数p阶群。则Γ(ZnG)为平面图当且仅当以下情形之一成立：①n=p=2；②n=p=3；③n=4，p=2；④n=3，p=2；⑤xp-1+…+x+1在Zn[x]中不可约，n=2，p≠2；⑥xp-1+…+x+1在Zn[x]中不可约，n=3，p≥5。

我们先给出两个有用的例子：

例1设Z2为模2剩余类环，G为2阶群，则Z2={0，1}，G={1，a}，Z2G={0，a，1，1+a}，Δ(G)={0，1+a}，D(Z2G(+)Δ(G))={(0，0)，(0，1+a)，(1+a，1+a)，(1+a，0)}。直接验证知，Γ(Z2G(+)Δ(G))为完全图K3，从而为平面图。

例2设Z3是模3剩余类环，G为2阶群，则Z3={0，1，2}，G={1，a}，Z3G={0，1，2，a，1+a，2+a，2a，1+2a，2+2a}，D(Z3G)={0，1+a，2+a，1+2a，2+2a}，Δ(G)={0，2+a，1+2a}，D(Z3G(+)Δ(G))={(0，0)，(0，2+a)，(0，1+2a)，(2+a，1+2a)，(1+2a，2+a)，(1+a，0)，(2+a，0)，(1+2a，0)，(2+2a，0)，(1+a，2+a)，(2+a，2+a)，(2+2a，2+a)，(1+a，1+2a)，(1+2a，1+2a)，(2+2a，1+2a)，(1，1+2a)，(2，2+a)，(a，2+a)，(2a，1+2a)}。我们得到Γ(Z3G(+)Δ(G))如图1所示，不难看出Γ(Z3G(+)Δ(G))是由每个三分类中均有两个顶点的1个完全三部图和3个完全二分图K2，4衔接而成。因为Γ(Z3G(+)Δ(G))含有K3，3的剖分图，如图2所示，所以Γ(Z3G(+)Δ(G))是非平面图。

下面我们给出Γ(Z3G(+)Δ(G))的平面性的一个刻画：

定理2设Zn为模n剩余类环，G为素数p阶群，Δ(G)为群环ZnG的增广理想，则Γ(ZnG(+)Δ(G))为平面图当且仅当n=p=2。

证明由于Γ(ZnG)与Γ(ZnG(+)Δ(G))的一个子图同构，因此若Γ(ZnG)为非平面图，则Γ(ZnG(+)Δ(G))必为非平面图。由引理3知，我们只须考虑以下6种情况：①n=p=2；②n=p=3；③n=4，p=2；④n=3，p=2；⑤xp-1+…+x+1在Zn[x]中不可约，n=2，p≠2；⑥xp-1+…+x+1在Zn[x]中不可约，n=3，p≥5。又Γ(ZnG(+)Δ(G))含有子图K|Δ(G)|-1，|Δ(G)|-1，从而若|Δ(G)|≥4，由引理2得，Γ(ZnG(+)Δ(G))必为非平面图。直接计算知：在①中，|Δ(G)|=2；在②中，|Δ(G)|=9；在③中，|Δ(G)|=4；在④中，|Δ(G)|=3；在⑤中，|Δ(G)|≥4；在⑥中，|Δ(G)|≥81。因此，我们只须考虑①和④。由例1知，当n=p=2时，Γ(ZnG(+)Δ(G))为平面图；由例2知，当n=3，p=2时，Γ(ZnG(+)Δ(G))不是平面图。证毕。

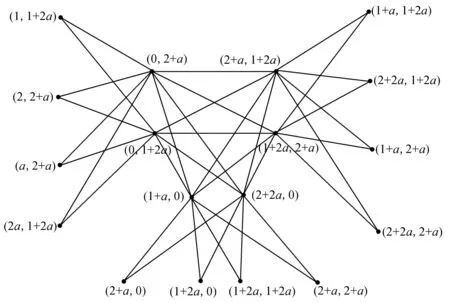
图1　Z3G(+)Δ(G)的零因子图Fig.1　The zero-divisor graph of Z3G(+)Δ(G)

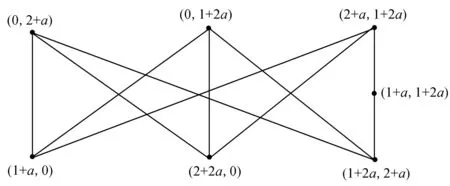
图2　K3，3的剖分图Fig.2　The subdivision graph of K3，3

3Γ(ZnG(+)Δ(G))的直径

在本节中，我们主要研究Γ(ZnG(+)Δ(G))的直径。由于ZnG(+)Δ(G)是有单位元(1，0)的交换环，从而Γ(ZnG(+)Δ(G))是连通图，且diam(Γ(ZnG(+)Δ(G)))≤3。又环ZnG(+)Δ(G)总含有非零零因子(0，a-1)，(a-1，1-a)，且d((0，a-1)，(a-1，1-a))=1，从而diam(Γ(ZnG(+)Δ(G)))≥1。因此diam(Γ(ZnG(+)Δ(G)))只能为1、2、3。

在文献[10]中，我们给出了群环ZnG的零因子图的直径的一个刻画。下面我们将从Γ(ZnG)的直径出发，利用分类讨论的方法，刻画Γ(ZnG(+)Δ(G))的直径。为了读者方便，我们将以引理的形式重新叙述文献[10]中的定理2。

引理4(文献[10]定理2)设Zn为模n剩余类环，G为素数p阶群。则：

①diam(Γ(ZnG))=0当且仅当n=p=2。

由文献[3]命题4.11知，如果diam(Γ(ZnG))=3，则diam(Γ(ZnG(+)Δ(G)))=3。因此，我们立刻获得以下结果：

命题1设ZnG为群环，Δ(G)为ZnG的增广理想，其中G为素数p阶群。如果引理4③的条件(a)、(b)、(c)中有一个成立，则diam(Γ(ZnG(+)Δ(G)))=3。

下面，我们分别予以刻画这4种情况。

命题2设Zn为模n剩余类环，G为素数p阶群，n=p，Δ(G)为群环ZnG的增广理想。则：

(a)当n=p=2时，diam(Γ(ZnG(+)Δ(G)))=1；

(b)当n=p且p≠2时，diam(Γ(ZnG(+)Δ(G)))=2。

证明当n=p=2时，由例1知，Γ(ZnG(+)Δ(G))为完全图K3，故此时diam(Γ(ZnG(+)Δ(G)))=1。当n=p且p≠2时，由引理4得，diam(Γ(ZnG))=2，故存在x，y∈D(ZnG)*，使得d(x，y)>1，进而d((x，0)，(y，0))>1，于是diam(Γ(ZnG(+)Δ(G)))≥2。由于当n=p时，ZnG为局部环，故D(ZnG)=Δ(G)，从而T2⊆T3。我们还注意到T4=∅。事实上，若(α，x)∈T4，则存在y∈Δ(G)*，使得y(α+x)=0，从而α+x∈D(ZnG)，进而α+x∈Δ(G)，而x∈Δ(G)，于是α∈D(ZnG)，矛盾。因此D(ZnG(+)Δ(G))*=T1∪T3。∀(0，x)，(0，y)∈T1，我们有路(0，x)—(x，-x)—(0，y)，故d((0，x)，(0，y))≤2；∀(α，x)，(β，y)∈T3，由于Δ(G)=〈a-1〉，其中〈a-1〉表示由a-1生成的ZnG的主理想，于是我们有一条路(α，x)—(ap-1+…+a+1，ap-1+…+a+1)—(β，y)，故d((α，x)，(β，y))≤2； ∀(0，x)∈T1，(β，y)∈T3，我们有路(0，x)—(ap-1+…+a+1，ap-1+…+a+1)—(β，y)，故d((0，x)，(β，y)) ≤2，从而diam(Γ(ZnG(+)Δ(G)))≤2。因此diam(Γ(ZnG(+)Δ(G)))=2。证毕。

命题3设Zn为模n剩余类环，G为素数p阶群，n=pk，k>1，Δ(G)为群环ZnG的增广理想，则diam(Γ(ZnG(+)Δ(G)))=2。

证明由引理4知，当n=pk，k>1时，diam(Γ(ZnG))=2，从而diam(Γ(ZnG(+)Δ(G)))≥2。由文献[11]推论2得，ZnG为局部环，其唯一极大理想m=IG+〈a-1〉，其中I为Zn的唯一极大理想，从而Δ(G)⊆D(ZnG)。由命题2的证明知：D(ZnG(+)Δ(G))*=T1∪T3，且∀(0，x)，(0，y)∈T1，d((0，x)，(0，y))≤2。∀(α，x)，(β，y)∈T3，我们有(α，x)—(pk-1(ap-1+…+a+1)，pk-1(ap-1+…+a+1))—(β，y)，故d((α，x)，(β，y))≤2；∀(0，x)∈T1，(β，y)∈T3，同理可证，d((0，x)，(β，y))≤2，从而diam(Γ(ZnG(+)Δ(G)))≤2。因此diam (Γ(ZnG(+)Δ(G)))=2。证毕。

命题4设Zn为模n剩余类环，G为2阶群，n为奇素数，Δ(G)为群环ZnG的增广理想，则diam(Γ(ZnG(+)Δ(G)))=3。

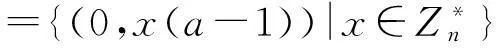
证明由文献[11]定理2知，ZnG是有两个极大理想的半局部环，设其极大理想为m1=〈a-1〉，m2=〈1+a+…+ap-1〉，则D(ZnG)=m1∪m2。首先证明：2+a2+a3+…+ap-1∉D(ZnG)。若2+a2+a3+…+ap-1∈m1，则存在xi∈Zn，0≤i≤p-1，使得

2+a2+a3+…+ap-1=(x0+x1a+…+xp-1ap-1)(a-1)=

(xp-1-x0)+(x0-x1)a+(x1-x2)a2+…+(xp-2-xp-1)ap-1，

从而有xp-1-x0=2，x0-x1=0，xj-xj+1=1，j=1，…，p-2，进而有x0-xp-1=p-2，于是p=0，这与n≠p矛盾；若2+a2+a3+…+ap-1∈m2，则存在yi∈Zn，0≤i≤p-1，使得2+a2+a3+…+ap-1=(y0+y1a+…+yp-1ap-1)(1+a+…+ap-1)，由于等式右边每一个ai的系数均为y0+y1+…+yp-1，矛盾。因此2+a2+a3+…+ap-1∉D(ZnG) 。由于Δ(G)=〈a-1〉，并注意到(a-1)((2+a2+a3+…+ap-1)+(a-1))=ap-1=0，从而 (2+a2+a3+…+ap-1，a-1)∈T4。直接验证知，Ann(2+a2+a3+…+ap-1，a-1)={(0，x)|x∈Δ(G)*}。∀x∈Δ(G)*，由文献[10]引理5得，(a-1)x≠0，从而(a-1，0)(0，x)=(0，(a-1)x)≠ (0，0)，从而d((2+a2+a3+…+ap-1，a-1)，(a-1，0))=3。因此diam(Γ(ZnG(+)Δ(G)))=3。证毕。

综合命题1～5，我们给出群环ZnG的理想化ZnG(+)Δ(G)的零因子图的直径的一个刻画：

定理3设Zn为模n剩余类环，G为素数p阶群，Δ(G)为群环ZnG的增广理想。则：

①diam(Γ(ZnG(+)Δ(G)))=1当且仅当n=p=2。

②diam(Γ(ZnG(+)Δ(G)))=2当且仅当以下条件之一成立：(a)n=p且p≠2；(b)n=pk，k>1。

③diam(Γ(ZnG(+)Δ(G)))=3当且仅当以下条件之一成立：(a)(p，n)=1；(b)n=pkq，q>1，(p，q)=1，k≥1。

注综合定理3和引理4，我们不难得到diam(Γ(ZnG))和diam(Γ(ZnG(+)Δ(G)))之间的关系：设Zn为模n剩余类环，G为素数p阶群，Δ(G)为群环ZnG的增广理想，则diam(Γ(ZnG(+)Δ(G)))≥diam(Γ(ZnG))。具体地，如果diam(Γ(ZnG))=0，则diam(Γ(ZnG(+)Δ(G)))=1； 如果diam(Γ(ZnG))=2，则diam(Γ(ZnG(+)Δ(G)))=2或3；如果diam(Γ(ZnG))=3，则diam(Γ(ZnG(+)Δ(G)))=3。在这里，我们给出一个diam(Γ(ZnG))和diam(Γ(ZnG(+)Δ(G)))不相等的例子：取Zn为模3剩余类环，G为2阶群，则diam(Γ(ZnG))=2，diam(Γ(ZnG(+)Δ(G)))=3。

参考文献：

[1]ANDERSON D F，LIVINGSTON P S.The zero-divisor graph of a commutative ring[J]. J Algebra，1999，217(2)：434-447. DOI:10.1006/jabr.1998.7840.

[2]AXTEL M，STICKLES J.Zero-divisor graphs of idealizations[J]. J Pure Appl Algebra，2006，204(2)：235-243. DOI:10.1016/j.jpaa.2005.04.004.

[3]MAIMANI H R，YASSEMI S.Zero-divisor graphs of amalgamated duplication of a ring along an ideal[J]. J Pure Appl Algebra，2008，212(1)：168-174. DOI:10.1016/j.jpaa.2007.05.015.

[4]LUCAS T G.The diameter of a zero divisor graph[J].J Algebra，2006，301(1)：174-193. DOI:10.1016/j.jalgebra.2006.01.019.

[5]ANDERSON D F，MULAY S B.On the diameter and girth of a zero-divisor graph[J]. J Pure Appl Algebra，2007，210(2)：543-550. DOI:10.1016/j.jpaa.2006.10.007.

[6]AKBARI S，MAIMANI H R，YASSEMI S.When a zero-divisor graph is planar or a completer-partite graph[J].J Algebra，2003，270(1)：169-180. DOI:10.1016/S0021-8693(03)00370-3.

[7]BELSHOFF R，CHAPMAN J.Planar zero-divisor graphs[J]. J Algebra，2007，316(1)：471-480. DOI:10.1016/j.jalgebra.2007.01.049.

[8]AKBARIA S，MOHAMMADIAN A.On the zero-divisor graph of a commutative ring[J].J Algebra，2004，274(2)：847-855. DOI:10.1016/S0021-8693(03)00435-6.

[9]ANDERSON D F，BADAWI A.The total graph of a commutative ring[J].J Algebra，2008，320(7)：2706-2719. DOI:10.1016/j.jalgebra.2008.06.028.

[10]郭述锋，谢光明，易忠.群环ZnG的零因子图的性质[J].广西师范大学学报(自然科学版)，2015，33(2)：68-75. DOI:10.16088/j.issn.1001-6600.2015.02.011.

[11]郭述锋，徐承杰，易忠.群环ZnG的代数性质及其结构[J].广西师范大学学报(自然科学版)，2009，27(2)：42-45. DOI:10.16088/j.issn.1001-6600.2009.02.004.

[12]MILIES C P，SEHGAL S K. An Introduction to Group Rings [M].Dordrecht：Kluwer Academic Publishers，2002.

[13]BUCKLEY F，LEWINTER M.图论简明教程[M].李慧霸，王风芹，译.北京：清华大学出版社，2005.

(责任编辑黄勇)

Properties of Zero-divisor Graphs of Idealizations of Group RingsZnG

GUO Shufeng1，2，XIE Guangming2，YI Zhong2，3

(1.School of Mathematical Sciences，Capital Normal University，Beijing 100048，China；2.College of Mathematics and Statistics ，Guangxi Normal University，Guilin Guangxi 541004，China；3. Guilin University of Aerospace Technology ，Guilin Guangxi 541004，China)

Abstract:It is very important to understand the structure of the ring itself by studying the zero-divisor graph of a ring to clearly and intuitively describe the structure of its zero-divisors by means of graph. Let G be a cyclic group of prime order， ZnG group rings of G over Zn and Δ(G)augmentation ideals of ZnG. Properties of zero-divisor graphs of idealizations of ZnG with respect to Δ(G) are discussed in this paper. It provides detailed descriptions of the girth，the diameter and the planarity of zero-divisor graphs of idealizations of ZnG，respectively.

Keywords:group ring； zero-divisor graph； girth； diameter； planarity

中图分类号：O153.3

文献标志码：A

文章编号：1001-6600(2016)01-0066-06

基金项目：国家自然科学基金资助项目(11161005)；北京市教育委员会科技计划重点项目(KZ201410028033)

收稿日期：2015-07-27

doi:10.16088/j.issn.1001-6600.2016.01.010

通信联系人：易忠(1961—)，男，湖南长沙人，广西师范大学硕士研究生导师，桂林航天工业学院教授，博士。E-mail：yizhong66@126.com