无招胜有招
罗桥生
我们知道,在教学方法上有这样的规律:教学有法,但无定法,贵在得法,教师事先预设的教法,只能作为备案。走进课堂,教师面对的是一个个鲜活的生命体,教师不能无视学生所呈现的生命信息来选择教法。而教学的方法的选择受到多方面因素的制约,如:教学内容的特点、学生知识水平和个性的差异、教师自身的素质与能力以及学校现有的客观条件等。只有教师明察课堂,适时调控,灵活选择切实可行的方法,才能有好的教学结果。
同样的,教学模式也有类似的说法,教有模式,但无定式,贵在得法。教学模式反映的是教学结构中教师、学生、教材三要素之间的组合关系,揭示了教学结构中各阶段、环节、步骤之间纵向关系以及构成课堂教学的教学内容、教学模式、教学手段、教学目标等因素之间的横向关系,表现为影响教学目标达成的诸要素在一定时空结构内某一教学环节中的组合方式。
因此,教学模式的选择,也应该根据教学内容的特点,教学目标的达成,教学手段的使用,教学方法的选择,学生的知识水平以及教师自己的教学特长以及学校的现有的客观条件等因素来决定。所以在选择模式上,即使是同一内容,其模式也不一定是完全固定不变的。
同时教学模式在一定时期内,在相同的理论框架下,教学模式在结构和方法上,具有一定的稳定性,同时也具有发展性,其稳定性体现在教学模式的变化不一定很大,但由于受多方面因素的影响,也不是一成不变的,也有发展性的一面。要把稳定性和发展性有机的结合起来,根据具体的情况选择合适的教学模式。下面我们就对同一节内容在不同时期、不同背景下,对教学模式的选择上进行一些比较。
因此教学模式和目标达成之间要达到一种默契的程度,既不能忽视教学模式的存在,也不能只重视教学模式,而不管目标达成与否,应该让教学模式与教学目标完美的结合起来,做到教学有模式,但无绝对的固定的模式。教学就像习武一样,新教师就要像刚学武术的人一样,讲究“一招一式”每一种课型都要有一种相对固定的模式,不同的课型要有不同的教学模式,就像初习武者要按老师教的一招一式进行比划,这是习武的初级阶段,教学的初级阶段也是这样;一旦教师对教材比较熟悉了,而在教学上也比较有经验了,能较好的驾驭课堂了,如果你是这一阶层的老师,就能灵活应用教学模式,并使之与教学目标、教学方法、教学手段、学生学情等很好的结合起来;而如果你是经验丰富的教师,这时就像习武者到达了其最高境界“无招胜有招。”这时的教者就不一定要拘泥于一招一式了,不一定要有固定的教学模式了,而应该是把教学模式和教学方法、教学目标等融为一体,紧紧围绕学生的教学目标的达成情况而展开教学,此时的教学就能随机应变,根据学生的情况去调整自己的教学方法和教学模式了,达到一种最高境界:“无招胜有招”。
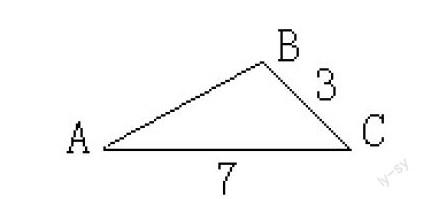
下面我们通过对几个案例进行分析比较,我们不难发现一些问题:锐角三角函数、同位角、内错角、同旁内角同样是概念课,但是在教学模式的处理上就不一样,因为同位角、内错角、同旁内角这节课里有三个概念,而这三个概念类似,教师如果采取三个概念同样对待,则显得比较呆滞,没有充分发挥学生的主观能动性,既表现出对学生的不信任,同时可能有教师“一言堂”的嫌疑,如果采用类比教学法,教师先精讲同位角这个概念,当学生充分理解了这个概念之后,教师再引导学生观察图形,并思考在三线八角中除了同位角外,有没有其他位置关系与同位角不一样的,又是怎么定义内错角和同旁内角的,这时教师出示事先拟好的学案,让学生根据学案先去自学,然后小组讨论,讨论完后再由学生发表自己的看法,教师针对学生的问题进行适当的点拨和总结,再让学生独立完成课堂作业,发现问题再提出来让学生发表看法,这样处理学生的参与程度高,积极性强,小组合作充分,取得的效果比教师的“一言堂”肯定要好;而锐角三角函数的教学,学生难以理解的就是其三角函数值与锐角之间是一种函数关系,只跟角的大小有关,与三角形的形状无关,要让学生理解这点,就必须通过一系列的角从特殊到一般的情况变化,让学生感受到比值只与角的大小有关,与三角形的形状无关,然后还要通过一定量的练习,让学生在做题中纠错,如:如图3:求sinA= (注∠A=30°)
很多同学就认为是3比7.造成这种结果的,既说明他们对锐角三角函数的条件不清楚,更主要的是他们对三角函数值的大小只与角的大小有关,当角的大小确定了,其三角函数值也就确定了,与三角形的形状是没有关系的。
总之,教学模式对于不同的教师、不同的课型、要采取不一样的模式,同时,模式的选择也要根据教学内容、教学方法、教学手段、教学目标、教师自己的教学特长以及学生的实际来确定,并且,同一个教师在不同时期,由于驾驭课堂的能力和对教材的理解上的不同,采用的教学模式也不尽相同,即使在同一时期,同一课题由于学生的不同,也要相应的进行变化,所以还是那句老话:教学的最高境界是教学有法,但无定法,贵在得法;教有模式,但无定式,贵在得法,即做到“无招胜有招”。

