确定带电粒子在磁场中做圆运动的圆心的方法

吴洪翔

摘要：带电粒子在磁场中圆运动的问题综合性较强，是高中物理的一个难点，也是高考的热点。解决这类问题既要用到物理中的洛仑兹力、圆周运动的规律，又要用到数学中的平面几何知识。其中，关键是确定圆运动的圆心，只有找到圆心的位置，才能正确运用物理规律和数学知识。在本文中，笔者将给出几种找圆心常用的方法。

关键词：物理教学；带电粒子；圆运动；确定圆心的方法

中图分类号：G633.7 文献标识码：A 文章编号：1992-7711（2016）06-0099

方法一：利用两个速度垂线的交点找圆心

由于向心力的方向与线速度方向互相垂直，洛伦兹力（向心力）沿半径指向圆心，知道两个速度的方向，画出粒子轨迹上两个对应的洛伦兹力，其延长线的交点即为圆心。

例1.如图1所示，一个质量为m电荷量为q的带电粒子从x轴上的P（a，0）点以速度v，沿与x正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴射出第一象限。求匀强磁场的磁感应强度B和射出点的坐标。

解析：分别由射入、射出点做两条与速度垂直的线段，其交点O即为粒子做圆运动的圆心，由图可以看出，轨道半径为：

例2. 电视机的显像管中，电子束的偏转是用磁偏转技术实现的。电子束经过电压为U的加速电场后，进入一圆形匀强磁场区，如图1所示，磁场方向垂直于圆面，磁场区的中心为O，半径为r，当不加磁场时，电子束将通过O点而打到屏幕的中心M点。为了让电子束射到屏幕边缘P，需要加磁场，使电子束偏转一已知角度，则此时磁场的磁感应强度B应为多少？

解析：电子先经过加速电场获得一定的速度，然后垂直于磁场方向进入磁场，不考虑电子重力的影响，电子在洛仑兹力的作用下在匀强磁场中做圆周运动，圆周上的两点a、b分别为进入和射出磁场的点。作电子a、b在二点速度νa、νb的垂线，交点O1即为轨迹圆的圆心，如图2所示。设电子的质量为m，电量为e，电子进入磁场时的速度为v，在磁场中做圆周运动的半径为R。电子在电场中加速，有eU=mν2/2

由牛顿第二定律和洛仑兹力公式有eνB=mν2/R

方法二：利用速度的垂线与弦的中垂线的交点找圆心

带电粒子在匀强磁场中做匀速运动时，如果已知轨迹上的两点的位置和其中一点的速度方向，可用联结这两点的弦的中垂线与一条半径的交点确定圆心的位置。

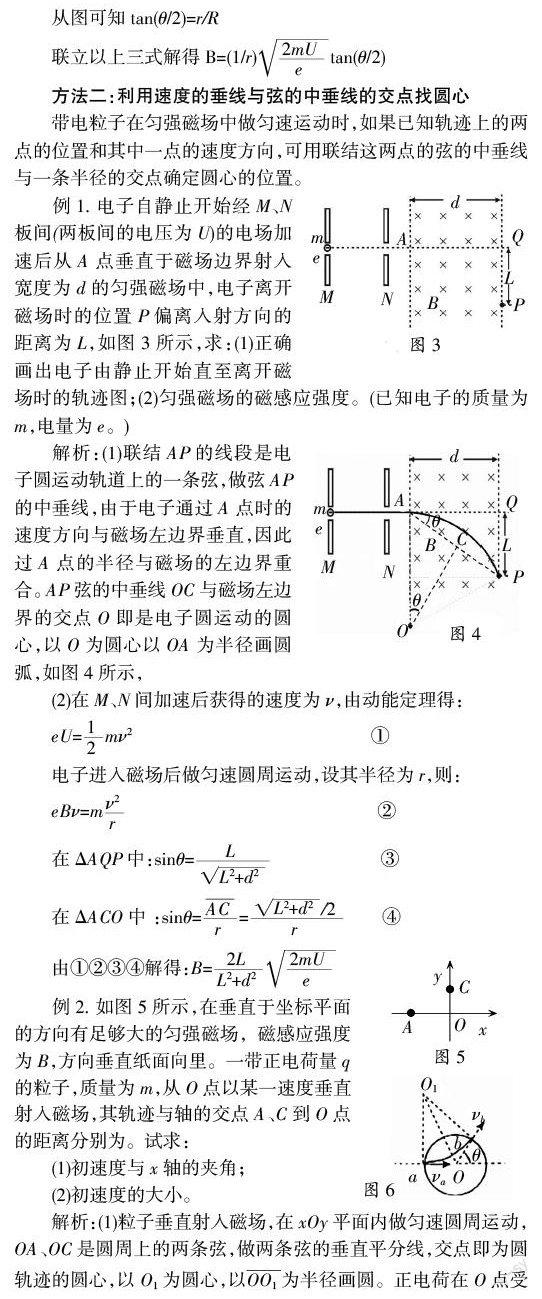
例1. 电子自静止开始经M、N板间（两板间的电压为U）的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中，电子离开磁场时的位置P偏离入射方向的距离为L，如图3所示，求：（1）正确画出电子由静止开始直至离开磁场时的轨迹图；（2）匀强磁场的磁感应强度。（已知电子的质量为m，电量为e。）

解析：（1）联结AP的线段是电子圆运动轨道上的一条弦，做弦AP的中垂线，由于电子通过A点时的速度方向与磁场左边界垂直，因此过A点的半径与磁场的左边界重合。AP弦的中垂线OC与磁场左边界的交点O即是电子圆运动的圆心，以O为圆心以OA为半径画圆弧，如图4所示，

（2）在M、N间加速后获得的速度为ν，由动能定理得：

例2. 如图5所示，在垂直于坐标平面的方向有足够大的匀强磁场，磁感应强度为B，方向垂直纸面向里。一带正电荷量q的粒子，质量为m，从O点以某一速度垂直射入磁场，其轨迹与轴的交点A、C到O点的距离分别为。试求：

（1）初速度与x轴的夹角；

（2）初速度的大小。

解析：（1）粒子垂直射入磁场，在xOy平面内做匀速圆周运动，OA、OC是圆周上的两条弦，做两条弦的垂直平分线，交点即为圆轨迹的圆心，以O1为圆心，以为半径画圆。正电荷在O点受到的洛仑兹力方向如图6所示。由左手定则知，粒子的初速度方向垂直于OO1斜向上。

设初速度为ν，与x轴的夹角为θ，由几何关系可知角∠O1OC=θ，故有：tanθ=（a/2）/（b/2）=a/b，θ=arctan（a/b）

（2）据图可知，电子的轨道半径：

方法三：利用速度的垂线与角的平分线的交点找圆心

当带电粒子通过圆形磁场区后又通过无场区，如果只知道射入和射出时的速度的方向和射入时的位置，而不知道射出点的位置，应当利用角的平分线和半径的交点确定圆心。

例1.一质量为m，带电量为+q 的粒子以速度v 从O点沿y 轴正方向射入磁感应强度为B 的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从B 处穿过x轴，速度方向与x 轴正方向的夹角为30°，同时进入场强为E、方向沿与x轴负方向成60°角斜向下的匀强电场中，通过了B点正下方的C点。如图示4所示，不计重力，试求：

（1）圆形匀强磁场区域的最小面积；

（2）C点到B点的距离h。

解析：（1）反向延长νb交y轴于O2点，作∠BO2O的角平分线交x轴于O1，O1即为圆运动轨道的圆心，OO1即为圆运动轨道的半径，

方法四：两洛仑兹力作用线的延长线的交点即为圆心

例1. 如图所示，有垂直纸面向外的匀强磁场，磁感应强度为B。在匀强磁场中做匀速圆周运动的一个电子动量为P，电荷量为e，在A、C点，所受洛仑兹力的方向如图9所示。已知，求电子从A运动到C的过程中的偏转角。

解析：A、C为圆周上的两点，做洛仑兹力作用线的延长线，交点O即为电子的圆周轨迹的圆心。以O为圆心、R=OA为半径作出电子从A到C的运动轨迹，标出电子在A、C两点的速度方向，它们的夹角即为偏转角θ，如图10所示。由几何关系有：

sin（θ/2）=（d/2）/R

由牛顿第二定律及洛仑兹力公式有

eνB=mν2/R

由动量的定义式有

P=mν

由以上三式解得

θ=2arcsin[（deB）/2P]

对复杂的问题，还可将上述三种方法综合运用。

（作者单位：四川省南部中学 637300）