浅谈勾股定理在中学数学中的应用

文艺蓉

【摘 要】勾股定理又称毕达哥拉斯定理，它有着悠久的历史，曾引起很多人的兴趣，它是中学数学中非常重要的一个定理。勾股定理很好地解释了直角三角形中三条边之间的数量关系，对于几何学中有关直角三角形的计算及证明问题，利用勾股定理往往能够迎刃而解，使学生快速掌握解决方法。同时，在实际生活中，勾股定理的应用也非常广泛。因此，在中学数学教学过程中，充分利用好勾股定理这一有效手段进行解题就显得尤为重要。本文将结合平时教学经验，对中学数学中的勾股定理的应用进行分析与探究，希望对读者有所帮助。

【关键词】勾股定理；直角三角形；应用

勾股定理在中学数学中有广泛应用，下面，我将对勾股定理在线段求长问题中的应用、在折叠问题中的应用、在证明过程中的应用以及在实际问题中的应用进行分析与探究。

一、勾股定理在线段求长问题中的应用

在初中数学中，一些线段求长问题使用常规方法解决非常困难，但使用勾股定理往往比较简单。

例1、如图，在中，于点D，AB=10，BD=8，DC2=13，求AC的长。

分析：图中△ABD与△ACD均为直角三角形，可利用勾股定理求出AD的长，从而求出AC的长。

二、勾股定理在折叠问题中的应用

解决折叠问题的关键是明确折叠后的图形与原图形关于折痕成轴对称，从而抓住折叠前与折叠后两图形全等来寻找条件，从而建立方程求解。

例2、现有一长方形纸片ABCD，在剪纸过程中需要折叠。如图所示，将△ADE沿AE折叠，使点D恰好落在BC边上的点F处。已知AB=8，BC=10，求EC的长。

分析：由折叠的性质知，AD=AF，DE=EF，据此可求AF的长。在Rt△ABF中，已知AF、AB的长，可求出BF的长，继而求出FC的长。而EC在Rt△ECF中，已知FC的长，由EF+EC=8，可将EC视为未知数，结合方程与勾股定理求解。

三、勾股定理在证明过程中的应用

这类问题的关键是找出直角三角形，利用勾股定理进行转化。

四、勾股定理在实际问题中的应用

勾股定理与日常生活有着广泛的联系，是中学数学考试内容之一。解决这类问题的关键是将实际问题转化为数学问题，画出图形，找出已知条件，最后得出答案。

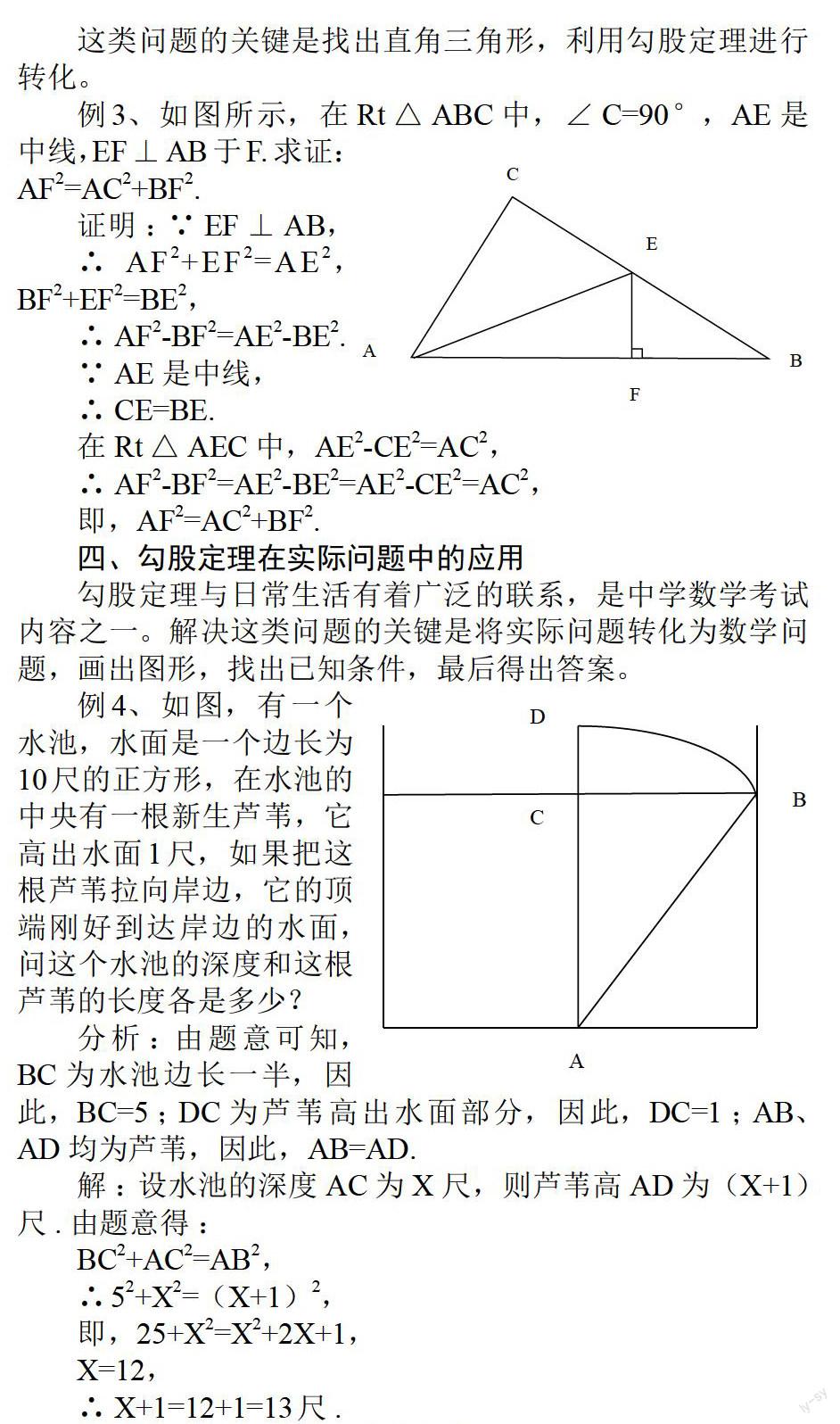
例4、如图，有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生芦苇，它高出水面1尺，如果把这根芦苇拉向岸边，它的顶端刚好到达岸边的水面，问这个水池的深度和这根芦苇的长度各是多少？

分析：由题意可知，BC为水池边长一半，因此，BC=5；DC为芦苇高出水面部分，因此，DC=1；AB、AD均为芦苇，因此，AB=AD.

解：设水池的深度AC为X尺，则芦苇高AD为（X+1）尺.由题意得：

數学思想和方法是数学的灵魂，是知识转化为能力的桥梁，勾股定理单独命题的题目较少，常与其他知识综合在一起考察，在中学数学试卷中常见题型是填空题，选择题和较简单的解答题。

总之，勾股定理的应用非常广泛，包括了理论与实际生活中的问题，是许多知识的的桥梁，因此，重视勾股定理的运用，对提高解题能力具有重要意义。