课堂因例题而精彩

顾秋芬

摘 要：数学课堂例题的选择在数学教学中起到了非常重要的作用，很多时候决定了一堂课的成败，因此我们应该重视例题的选择。

关键词：贴近生活；有趣味性；有探究性；有开放性

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2016）11-044-2

思考能让学生感受和体验数学知识的产生、发展和应用，能启发学生发现问题和提出问题。新课程标准强调，教师要转变教育观念和教学方式，鼓励学生质疑问题、探究，使数学成为再创造再发现的过程。因此数学教学应以学生发展为本，激发学生的学习兴趣，从学生实际出发，创设有助于学生学习的问题和情境，引导学生通过实践、思考、探索、交流等方式获得知识。而课堂教学是实现这一目标，达到这一要求的基本途径，是使学生数学技能和数学思维得到提高和发展的重要环节。因此课堂例题的选择就显得尤为重要，是课堂教学的关键，是数学课堂的生命。那么如何来选择课堂例题呢？

一、趣味例题最能激发学生的参与度

兴趣是参与的内驱力，是影响学习效率最主要的因素。新颖有趣的例题，能使学生兴趣盎然地投入到学习活动中，能稳定学生的注意力，深化学生的思维，激发学生学习的主动性和积极性。学生对所学知识产生浓厚的兴趣，在学习过程中获得成功的体验，就会主动参与数学学习活动。所以对学生来说，兴趣可以说是他的老师。因此激活学生的学习兴趣是我们老师应该做的头等大事，而如何来激发学生的学习兴趣就要根据学生的特点。实际上，初中生还是一些尚未脱离童话世界的孩童，他们最喜欢的很多偶像，还是童话世界中的人物。因此一些与童话有关的事物都能激起他们浓厚的兴趣。所以在选择例题的时候，与童话有关的有趣话题会比那些没有背景的纯粹讲解知识的例题要有效得多。例如下面的例题：

你读过《西游记》吗？如果你是一位细心的读者，那么你会发现这部文学名著中还包含着许多数学学问呢。下面是《西游记》中的一个情节：话说齐天大圣孙悟空在护送唐僧去西天取经的路上，有一次与妖魔相遇，妖魔喝道：“我数百年修炼才有今天，你小小年纪算个什么，快与我闪开！”这时孙悟空哈哈大笑着说：“你说我小，真是瞎了你的狗眼，你连我的孙子都够不上呢！你听着：老孙的四分之一是在花果山为王；后又上天当了二百九十年齐天大圣；因大闹天宫，被压在五行山下度过了年纪的一半；然后护送师父去西天取经，至今又有十年了。算算我有多大岁数！……亲爱的同学，你能求出孙悟空当时的岁数吗？

对于这样的例题，往往刚念完题，学生就会开始讨论，猜测，他们的思绪立刻会被题目所叙述的内容深深吸引。马上就会有同学埋头思索，或者用笔在纸上开始演算，甚至还有的会在嘴里叨唠着：大圣的年纪肯定很大。于是这时老师就可以提出问题：

（1）大圣的岁数能否算出？

（2）如果能够算，那么用什么方式来解决？

很多情况下学生都会七嘴八舌地在下面猜测回答，有的说能，有的说不能，根据情况老师就可以设时引导学生用方程来解题。

例如老师可以问：如果设大圣的岁数为X岁，则其年龄的四分之一，二分之一又可以怎样表示？能否用我们所学的方程来解决？

在此种情况下提出的问题，立刻能引起学生的兴致，激发了学生丰富的想象力和强烈的好奇心，提高了学生的学习兴趣。学生急切希望得到答案，又无法一步得到，引发了学生对问题作探索的迫切心理，使得学生的注意力和思维随老师的发问而深入，不断探索，直至把问题圆满解决，从而调动了学生学习的积极性。当然老师在设置问题的时候要由浅入深，由简到繁，要启发思路，介绍方法，引导学生参与，从而使学生的思维能力得到充分的发挥，体现自身价值，发挥课堂上的主体作用。

二、贴近生活的例题最能被学生接受

我们说数学来源于生活，因此贴近学生生活的例题是最能被学生所接受的，也是学生最感兴趣的话题。它能使学生积极参与数学活动，对数学产生强烈的兴趣，增强学生的学习动力。著名心理学家皮亚杰指出：“只有要求儿童作用于环境，其认识发展才能顺利进行。只有当儿童对环境中的刺激进行同化和顺应时，其认识结构的发展才能得到保障。”这就是说，从学生生活出发，从学生平时看得见、摸得着的周围事物开始，在具体、形象的感知中，学生才能真正认识数学知识。如下面的几例：

1.我市出租车收费标准为：起步价10元，3千米后每千米18元，5千米后为25元，当某人坐车X千米，他的收费是多少？如果收费为20元，则此人坐车里程为多少？

2.在一次社会实践的活动中，某校甲，乙，丙三个小组一同调查高峰时段苏州的人民路，干将路，东环路的车流量，他们在这几条上分别设点，记录每小时各点处通过的汽车辆数来观测车流量，三个小组汇报高峰时段的车流量情况时，都没有直接说出观察结果，而是提供了以下的信息。

甲组代表说：干将路车流量为每小时约1000辆；

乙组代表说：东环路比人民路的车流辆每小时约少1000辆

丙组代表说：人民路车流量的3倍与东环路车流量的差约是干将路车流量的2倍。

请根据他们所提供的信息，算算高峰时段人民路，东环路的车流量各是多少？

3.某地电话拨号入网有两种收费方式，用户可以任选其一

（A）计时制：005元/分

（B）包月制：50元/月（限一部个人住宅电话上网）

此外，每一种上网方式都得加收通信费002元/分，

（1）某用户上网时间为X小时，请你分别写出两种收费方式下，该用户应支付的费用。

（2）如果某用户估计一个月内上网时间为20小时，你认为采用哪一种方式较为合算？

以上几例都是贴近学生生活的数学问题，这样的问题就发生在学生的身边，学生都身有感触，很多时候作为老师不一定要自己先讲解，可以要求学生自己事先先做调查，在调查中寻找解决问题的方式方法，然后在课堂上大家交流，总结解决的方案。这样往往能使学生深刻地体会到数学就在我们身边，是我们看得见，感觉得到的东西，真实的存在着，无意间提高了学生在身边的实际问题中收集、加工数学信息，抽象概括数学问题，提高自我解决问题的能力。同时能深刻地感受到：数学教学，源于现实，用于现实。

三、探究性的例题最能让学生品尝到成就感

著名教育家苏霍姆林斯基说过：“在人的心灵深处，都有一种根深蒂固的需要，就是希望自己是一个探索者、发现者、研究者，而在儿童的精神世界中，这种需要特别强烈。”因此，教师在教学时应创设问题情境，激发学生想成为探索者、发现者、研究者的动机，鼓励学生超越自我、超越同学、超越老师。而数学教学中，探究性问题的设置就是要唤醒学生解决问题和激发学生探究的兴趣，使学生去尝试、猜测、实验、类比、推理、去合作交流。在教师的引导下，亲身体验知识的形成过程，获得数学必需知识，并解决问题，从而获得成就感。如下面的问题：

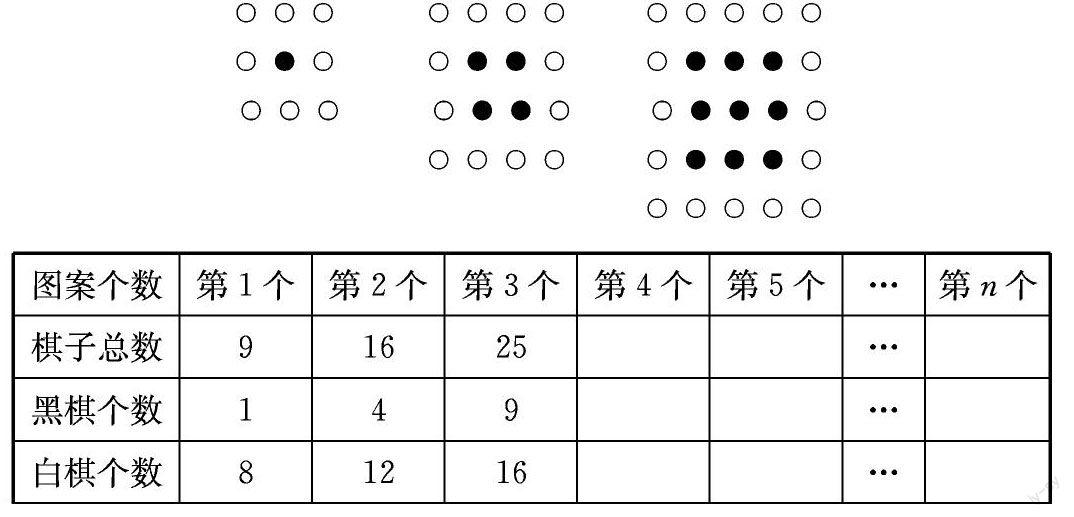
用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n个图案需要用白色棋子 枚（用含有n的代数式表示）。

这样的题如果让学生马上回答肯定会有一定的困难，老师可以让同学把事先准备好的黑白两色围棋拿出来，按照题目的意思摆放图案，同时完成下面的表格。

图案个数第1个第2个第3个第4个第5个…第n个

棋子总数91625…

黑棋个数149…

白棋个数81216…

同学们一边摆放棋子一边填写表格，同时老师提出问题：

（1）每个图案总棋子的摆放有什么规律？

（2）每个图案黑棋的摆放有什么规律？

（3）白棋个数与棋子总数、黑棋个数有什么关系？

学生通过表格以及自己摆放的棋子立马能得到下面的规律：

1.棋子总数为图案个数加2的平方

2.黑棋个数为图案个数的平方

3.白棋个数为棋子总数与黑棋个数之差。

所以根据学生自己动手探索很快得到了答案为：（n+2）2-n2。

由此可以看出此类题目能使学生明白：学习知识最重要的途径是学生自己去发现，因为这种发现理解最深，也最容易掌握其中的规律，让学生充分感受到发现问题和解决问题带来的愉悦，获得无限的成就感，充分调动了学生学习的积极性和主动性，增强了学生参与数学活动的意识，培养了学生的创新意识。

四、开放性的例题最能促进学生思维的发展

开放性试题是近年来经常出现，既注重知识又注重能力的好题目，反映了当前以创新教育为核心的素质教育的要求。前苏联著名数学教学专家B.A.奥加涅相认为：“区别于传统的教学，现代教学的特点在于力求控制教学过程以促进学生思维发展”。因此，我们必须把学生从不利于他们发展的“题海”中解放出来，精心设计能促进学生思维发展及其他素质发展的练习。而开放性练习题，能给学生提供更多的参与机会和成功机会，让学生从不同角度提出问题、思考问题、解决问题，有利于学生发散思维、求异思维、直觉思维的培养，有利于促进学生从模仿走向创新。由于开放性问题设置问题的开放性，必然带来问题内容的新颖性，问题形式的生动性，解决问题的发散性，能留给学生一个广阔的思维空间，从而能激发学生的创新意识，提高学生的创新思维，同时也能培养学生的创新能力，在素质教育中最具活力。例如下面的题目：

已知反比例函数y=k/2x和一次函数y=2x-1，其中一次函数的图象经过（a，b），（a+1，b+k）两点

（1）求反比例函数的解析式。

（2）如图，已知点A在第一象限，且同时在上述两个函数的图象上，求点A坐标。

（3）利用（2）的结果，请问：在X轴上是否存在点P，使△AOP为等腰三角形？若存在把符合条件的P点坐标都求出来；若不存在，请说明理由。

上述（1）、（2）两个问题相对来讲比较简单，很多同学都能够解答出来，但对于第（3）个却不是那么容易回答。老师可以设置一些问题引导学生思考：

（1）等腰△AOP有哪三条边？

（2）已知的边AO可以作为等腰△AOP的腰还是底？

（3）请同学自己在图上找出符合的点，然后进行班级讨论。

其实此题用到了数学中的分类思想，把AO作为等腰△AOP的腰和底，分别就腰和底寻找符合条件的点。以AO为腰可以找到三个符合条件的点，AO作为底可以找到一个符合条件的点。只要老师引导的合理，学生自己是能够获得答案的。

上述问题通常能留给学生很大的思维空间，能激起学生对这类问题积极探索的创新意识，提高学生的数学修养，如果作为考题也是最能反映学生的数学基础的。由此可以看出现代数学教学把发展学生的思维提到了相当高的地位，形象地把数学喻为“思维的体操”。

总之，数学教学要使数学活动与生活广泛联系，使学生能综合利用所学的知识解决问题，就应该让学生加深对知识的理解，学会利用数学思维解决问题的思考方法。而这些能力的提高和培养，只能利用平时的例题使学生慢慢地受熏陶，在潜移默化中形成数学修养，从而提高了数学课堂的效率。这是一个漫长而艰巨的过程，需要我们每一位教师悉心的培育，只有在你的尽心照料下，未来的树木才能长成栋梁。