“勾股定理”的教学课例分析

丁金华

【摘要】 勾股定理是直角三角形非常重要的性质，揭示了直角三角形的三边数量关系，主要解决直角三角形中的计算问题，它与实数、二次根式和方程知识联系密切，将来学习四边形、圆及一元二次方程后应用范围更大，勾股定理也是以后学“解直角三角形”的基础. 课例注重培养学生的分析思考能力，通过比较、探索、归纳理解勾股定理，以利于正确应用.

【关键词】 勾股定理；探索；归纳；直角三角形；面积；数量关系

下面是这节课的课堂实录及反思：

一、以问题解决方式导入新课

师：在我们认知过的三角形中，有哪些特殊的三角形？

生1：等边三角形； 生2：等腰三角形；生3：还有直角三角形.

师： 回答得很好. 那老师再追问等边三角形特殊在哪里？学生反映很快马上回答：三条边相等.

师：如果一个等边三角形的一条边为3，另外两条边是多少？生：3和3 .

师：很好，那等腰三角形的特殊性在哪里？生：有两条边相等.

师：已知一个等腰三角形的两边为3和4，另一边长是多少？生：3或4.

师：很聰明，抓住了等腰三角形的特征. 直角三角形也是特殊的三角形，如果已知两边为3和4，如何求第三边呢？有一学生答：第三边是5，因为我听过勾3股4弦5的说法.

师：其他同学会求吗？（摇头）好，这就是我们这节课要讨论的课题，反映直角三角形三边关系的著名定理：勾股定理. （板书课题：2.1勾股定理）

【设计意图】：从特殊三角形边的关系，引出一系列问题让学生思考，从而激发学生探索问题的兴趣，自然引出对直角三角形三边关系的探讨，因“疑”生“趣”，导入自然贴切，引起学生关注课堂学习.

二、定理探索（数学实验）

（一）简要介绍历史

师：直角三角形特殊在哪？学生回答：有一个角是直角.

师：有一个角是直角这个特殊性很显然. 但三边之间的关系很难发现，所以说勾股定理的发现是人类历史上伟大的发现. 大家一定想了解一点勾股定理的历史背景吧.

教师活动：幻灯片展示历史背景，教师做简单介绍，目的是让学生知道名称的由来，强调我国是最早发现勾股定理的国家之一，然后由一张邮票图案引发思考. （幻灯出示邮票图案）

师：这张图能反映直角三角形的三边关系吗？如果能，那三边之间到底是什么关系呢？我们一起来做数学实验.

【设计意图】通过介绍历史，让学生对勾股定理有一个感性认识，重点介绍我国是最早发现勾股定理的国家之一，培养学生的民族自豪感.

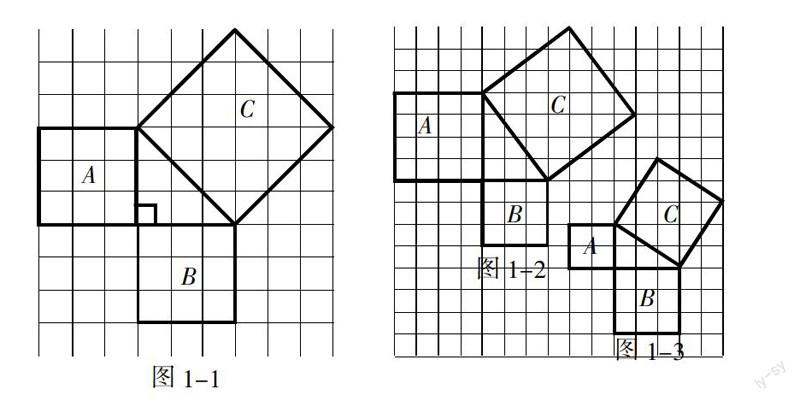
（二）数学实验：（每个小方格代表一个单位面积）

1. 等腰直角三角形的三边向外作正方形，根据右图图1-1填空. （幻灯显示）

（1）正方形A中含有（ ）个小方格，即A的面积是（ ）个单位面积；

（2）正方形B的面积有（ ）个单位面积；

（3）正方形C的面积（ ）个单位面积.

学生活动：学生观察图形思考后回答问题.

2. 一般直角三角形的三边向外作正方形，根据图形填空. （幻灯显示）

学生活动：学生观察图形思考后回答问题. 计算A和B的面积比较容易，如何计算C的面积？学生积极动脑，提出自己的想法，并上台来讲解自己的思路.

教师活动：动画展示C的面积的两种计算方法. 根据表格数据，能发现什么结论？从而归纳出正方形A、正方形B、正方形C之间的关系.

师生共同探讨得出结论：正方形A的面积 + 正方形B的面积=正方形C的面积

师：猜想直角三角形三边关系，正方形面积和直角三角形边之间存在什么关系？生：面积=边长的平方.

师：假设直角三角形两直角边为a，b斜边为c. 由以上计算结果，我们可以猜想直角三角形的三边满足什么等量关系呢？生：a2 + b2 = c2.

师：是不是所有的直角三角形都满足这一数量关系呢？我们都知道用具体数据归纳得出的结论并不能用来说明事实，还需要进一步论证. 这就需要我们对一般的直角三角形进行证明.到目前为止，对这个命题的证明方法已有五百种之多. 勾股定理是数学史乃至人类史上一个著名的定理. 它一直以来吸引着数学家、普通学者、一般百姓，甚至美国总统的兴趣. 人们目前共发现了它的500多种证法，勾股定理可能是人类史上，证明方法最多的一个定理.

【设计意图】通过数学实验探索直角三角形的三边关系，让学生感受勾股定理的几何意义，培养探究精神.

三、定理证明探索

介绍图形，这是我国数学家赵爽在证明勾股定理时用到的拼图. 这个图形熟悉吗？数学课本上就有.

设直角三角形两直角边短边为a，长边为b，斜边为c.

师：这个图形是由哪几个部分组成的？

生：有四个全等的直角三角形和一个正方形组成.

师：从哪个角度来分析这个图形？周长？面积？

学生开动脑筋，一名学生踊跃发言：周长很显然是4C，从周长角度找不到未知量之间的等量关系. 只有从面积角度来思考，因为一个图形不管怎么分割，它的面积总和是不变的.

师：说的很好. 整个图形是一个正方形，它的面积是C2，组成正方形的各部分面积可以表示为（b - a）2 + 4·ab. 从面积角度列出一个等式

C2 = （b - a）2 + 4·ab，（进一步追问：为什么相等？）教师启发：图中有空缺吗？有重叠部分吗？学生发现没有.

师：图形经过拼接后只要没有重叠，没有空隙，面积就不会改变. 教师用红粉笔画上一个等号，以引起学生注意. 上面等式经过整理得a2 + b2 = c2.

【设计意图】本环节是难点的突破环节，从图形拼接关系列出面积相等的数量关系，让学生感受数和形的结合.

勾股定理：在直角三角形中，两条直角边的平方和等于斜边的平方. （幻灯片出示）符号表示：在Rt△ABC中，∠C = 90°，a2 + b2 = c2.

师：运用定理要注意哪些方面？学生回答.

教师归纳板书：

1. 在直角三角形中

2. 式中的a、b表示两直角边长，c表示斜边的长度.

3. 等式反映的是2直角三角形三边的数量关系.

【设计意图】通过归纳注意点，让学生进一步知道勾股定理的具体内容.

四、例题的意图分析

例1：在Rt△ABC中，∠C = 90°.

（1）已知b = 4，a = 3，求c = ____.

（2）已知c = 13， b = 5，求a = ____.

【设计意图】通过教师的示范板书，教会学生如何运用勾股定理解题，引导学生规范解题.

五、随堂有效练习

1. 求下列直角三角形中未知边的长：

请学生扮演（3人）教师讲评板书中存在的问题.

2. 已知，四边形ABCD中，∠DAB = ∠DBC = 90°，AD = 3，AB = 4，BC = 12. 求：DC的长.

分析：（1）DC在直角三角形中吗？

（2）要求DC，需先求BD.

【设计意图】练习目的是巩固勾股定理的知识，也是检验课堂学习效果的有效途径.

六、课堂小结

师：本节课我们一起经历了做实验得出猜想，对猜想进行论证，最后运用勾股定理解决简单的数学问题的过程，同时也感受对于数学知识的学习要严谨. 课后我们还可以对勾股定理的历史，证明方法做进一步的探索学习，以获得更多关于勾股定理的知识.

七、拓展思考题

开头老师提出的问题，一个直角三角形的两直角边为3和4，那么另外一边是多少？请同学们重新思考，这个问题你能解决了吗？

已知：Rt△ABC中，AB = 4，AC = 3， 则BC的平方为 .

【设计意图】本题与引入的问题呼应，直角三角形三边都是特指的，这里没有指明直角边和斜边，目的是促使学生灵活运用勾股定理.

课例反思

本课例从以下几个方面设计：第一个环节从让学生回忆特殊三角形边的关系直接引出课题：勾股定理；第二个环节简要介绍勾股定理的历史背景，让学生感知古代人的聪明才智；第三个环节从一张邮票图案引出问题：这张图能反映直角三角形的三边关系吗？和学生一起探索做数学实验，滲透面积割补方法，得出猜想；第四个环节介绍我国数学家赵爽的拼图证明方法，引导学生从图形本身思考问题，从面积角度列出数量关系式，突破本节课的教学难点；第五个环节是知识的应用，例题注重知识的直接运用，练习有层次性；最后教师简单小结，并引导学生思考本课开头提出的问题，整节课首尾呼应，达到解决问题的根本目的.

【参考文献】

[1]徐国英.《勾股定理》教学设计及点评[J].中国信息技术教育，2009，19.