MATLAB仿真在自动控制理论教学中的应用

杨艳丽　郭一锋　张国良　王蜂

摘要：为了提高学生对《自动控制理论》这门课的学习兴趣，提高分析和设计自动控制系统的能力，本文采用MATLAB语言结合实例对自动控制理论课程中的一些典型问题进行了分析。通过这种方法，加深学生对自动控制理论这门课的理解程度，提高学生学习的积极主动性，改善教学效果。

关键词：自动控制原理；MATLAB语言

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2016）21-0266-02

一、引言

《自动控制理论》课程是支撑我校导航、制导与控制国家重点学科的主干课程，自1959年起为测控工程专业学员开设，目前已面向全院本科学员，是全院性的专业基础课，在整个专业知识体系中占据非常重要的地位，具有承上启下的作用。该课程涉及数学、物理、电子、机械等多学科领域，同时还与实际工程系统的控制密切相关，具有内容丰富、理论性强、涉及知识面广、更新发展快等特点，有一定的深度和学习难度。学生在学习过程中容易感到枯燥乏味，产生厌学情绪。在历年的学习过程中，都需要进行大量、复杂的计算以及绘制复杂的图形，如果运用MATLAB在仿真环境下可极其方便地对系统性能进行分析，观察系统的各种曲线和性能指标非常直观，可以使学生对所学理论知识有更深刻的理解和把握，有效地提高教学质量。时域分析、频域分析和根轨迹分析是经典控制理论的三个重点内容，下面将通过三个实例详细说明MATLAB在教学中的应用。

二、二阶系统的时域分析

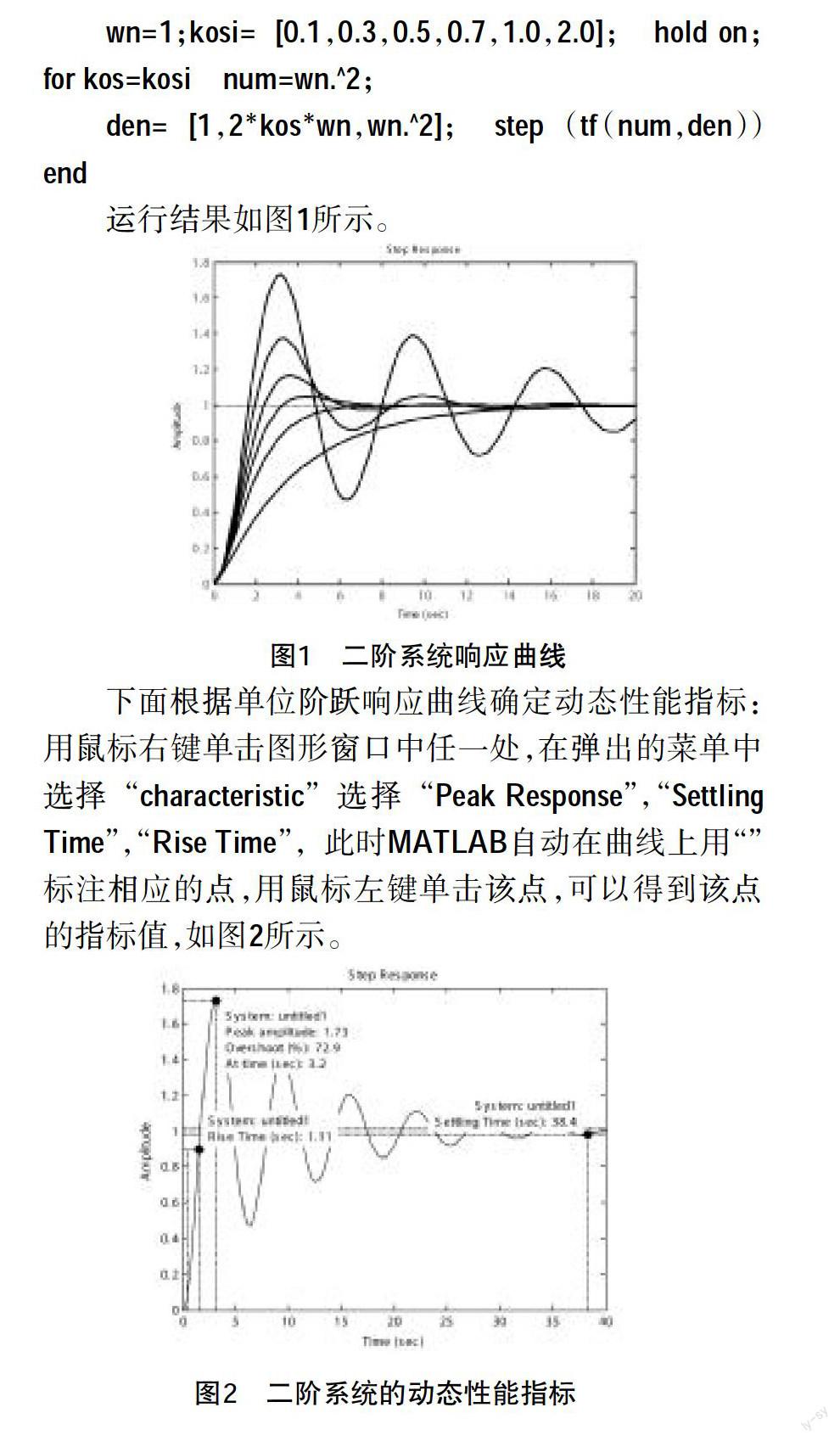
运行结果如图1所示。

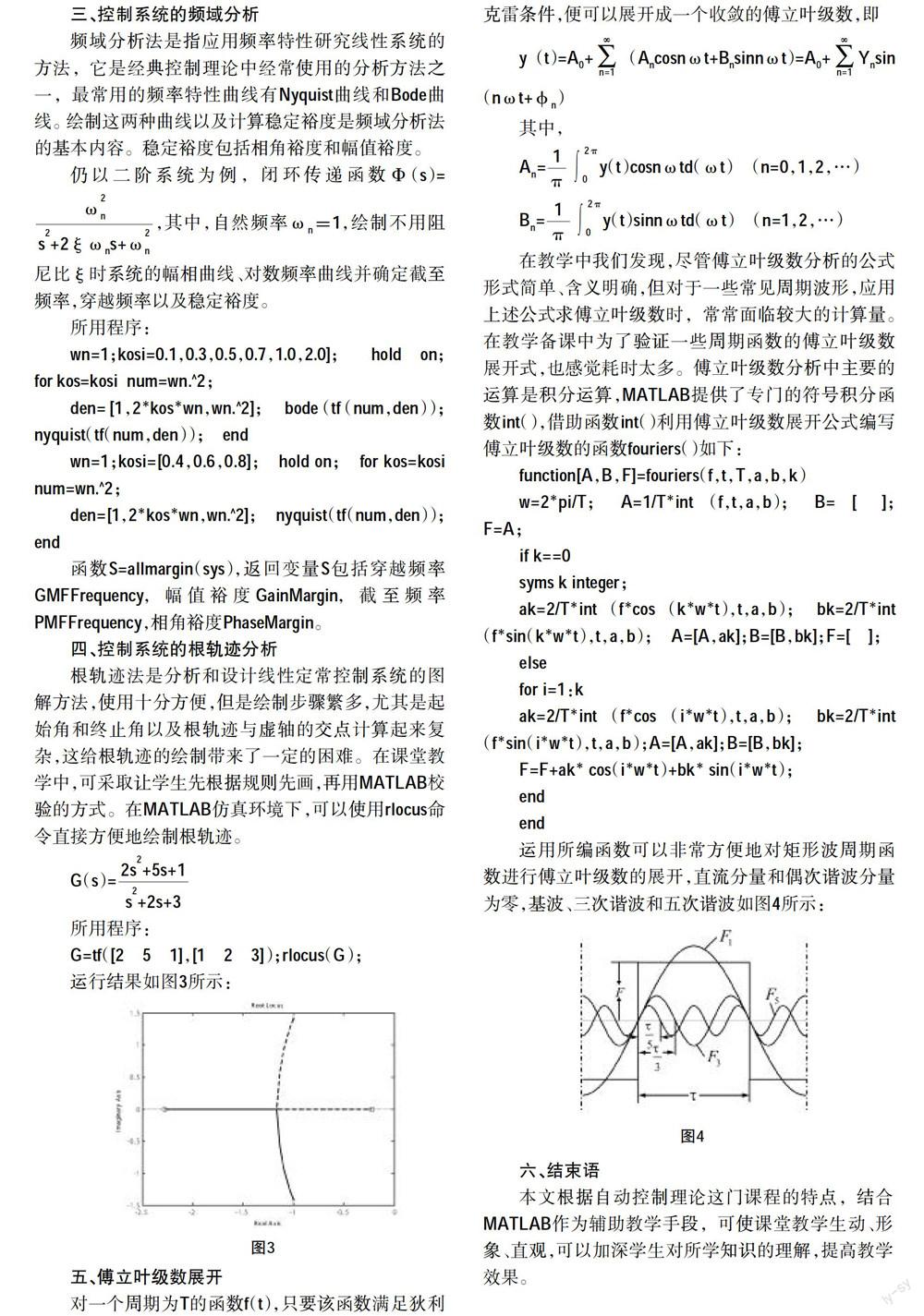
下面根据单位阶跃响应曲线确定动态性能指标：用鼠标右键单击图形窗口中任一处，在弹出的菜单中选择“characteristic”选择“Peak Response”，“Settling Time”，“Rise Time”，此时MATLAB自动在曲线上用“”标注相应的点，用鼠标左键单击该点，可以得到该点的指标值，如图2所示。

三、控制系统的频域分析

频域分析法是指应用频率特性研究线性系统的方法，它是经典控制理论中经常使用的分析方法之一，最常用的频率特性曲线有Nyquist曲线和Bode曲线。绘制这两种曲线以及计算稳定裕度是频域分析法的基本内容。稳定裕度包括相角裕度和幅值裕度。

所用程序：

wn=1；kosi=0.1，0.3，0.5，0.7，1.0，2.0]； hold on； for kos=kosi num=wn.^2；

den=[1，2*kos*wn，wn.^2]； bode（tf（num，den））； nyquist（tf（num，den））； end

wn=1；kosi=[0.4，0.6，0.8]； hold on； for kos=kosi num=wn.^2；

den=[1，2*kos*wn，wn.^2]； nyquist（tf（num，den））； end

函数S=allmargin（sys），返回变量S包括穿越频率GMFFrequency，幅值裕度GainMargin，截至频率PMFFrequency，相角裕度PhaseMargin。

四、控制系统的根轨迹分析

根轨迹法是分析和设计线性定常控制系统的图解方法，使用十分方便，但是绘制步骤繁多，尤其是起始角和终止角以及根轨迹与虚轴的交点计算起来复杂，这给根轨迹的绘制带来了一定的困难。在课堂教学中，可采取让学生先根据规则先画，再用MATLAB校验的方式。在MATLAB仿真环境下，可以使用rlocus命令直接方便地绘制根轨迹。

运行结果如图3所示：

五、傅立叶级数展开

对一个周期为T的函数f（t），只要该函数满足狄利克雷条件，便可以展开成一个收敛的傅立叶级数，即

在教学中我们发现，尽管傅立叶级数分析的公式形式简单、含义明确，但对于一些常见周期波形，应用上述公式求傅立叶级数时，常常面临较大的计算量。在教学备课中为了验证一些周期函数的傅立叶级数展开式，也感觉耗时太多。傅立叶级数分析中主要的运算是积分运算，MATLAB提供了专门的符号积分函数int（），借助函数int（）利用傅立叶级数展开公式编写傅立叶级数的函数fouriers（）如下：

function[A，B，F]=fouriers（f，t，T，a，b，k）

w=2*pi/T； A=1/T*int（f，t，a，b）； B=[ ]； F=A；

if k==0

syms k integer；

ak=2/T*int（f*cos（k*w*t），t，a，b）； bk=2/T*int（f*sin（k*w*t），t，a，b）； A=[A，ak]；B=[B，bk]；F=[ ]；

else

for i=1：k

ak=2/T*int（f*cos（i*w*t），t，a，b）； bk=2/T*int（f*sin（i*w*t），t，a，b）；A=[A，ak]；B=[B，bk]；

F=F+ak* cos（i*w*t）+bk* sin（i*w*t）；

end

end

运用所编函数可以非常方便地对矩形波周期函数进行傅立叶级数的展开，直流分量和偶次谐波分量为零，基波、三次谐波和五次谐波如图4所示：

六、结束语

本文根据自动控制理论这门课程的特点，结合MATLAB作为辅助教学手段，可使课堂教学生动、形象、直观，可以加深学生对所学知识的理解，提高教学效果。