四川北部山区输电线路工程可研投资估算模型研究

李丽 王国珍 黄善领

摘要：四川北部山区输电线路工程具有独特性。一种简洁有效的可研投资估算方法和模型在理论上和实际工作中都意义重大。神经网络的非线性、自学习的特点，非常适合建立输电线路工程的投资估算模型。模型选取电压等级、线路长度、导线截面等8个输入变量，建立三层神经网络结构，用收集的训练样本训练神经网络模型，测试样本测试模型。测试结果表明模型效果良好。模型使用者无需掌握过多技术细节，适合于投资发展部门估算，前景良好。

关键词：输电线路工程；投资估算；神经网络；可研；预测

一、引言

投资估算是投资决策过程中确定融资方案、筹措资金的重要依据，对项目决策、项目管理、质量控制意义重大。

山区电网建设对当地经济和社会发展十分重要，线路工程是电网建设工程中的重要组成部分。四川北部山区，主要为山地，并向盆地过渡，气候复杂多变，秋冬季线路多覆冰，风速较大。特殊的地形和气候使得输电线路的建设难度和工程造价增加。一种科学的、合理的输电工程投资估算方法，对电网工程有益。

对于工程投资的快速估算，国内外都有一些相应的研究。国外有人采用成本估算的方法，建立工程成本的数据库，根据历史工程、类似工程的历史资料，结合相应的参考指标手册，用类比、回归的方法确定拟建工程的投资情况；也有人利用典型工程建设经验，将模糊数学引入工程造价进行投资估计，提高计算速度，减少了计算周期；还有人采用相似工程法来估算投资，但其主观性强。这些方法都要求估算者对工程本身和相应技术有较高的了解，但实际各地市电力公司的投资决策部门，多侧重经济和管理专业背景，因此，如果有一种简洁有效的方法和模型帮助进行变电站工程可研投资估算，将对投资决策和规划有很大帮助。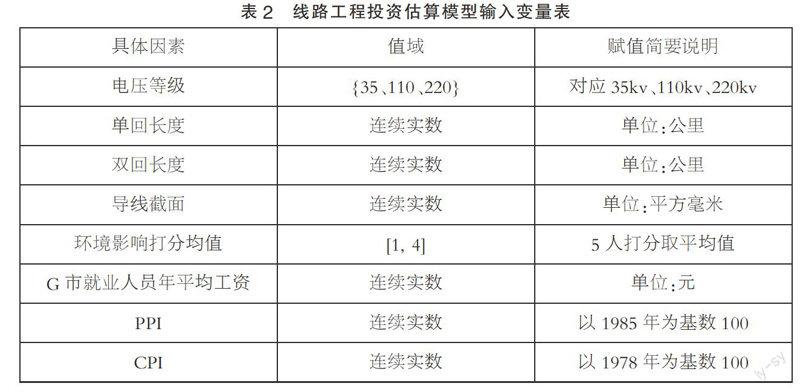

此篇论文，在收集对应的输电线路工程估算的历史数据基础上，采用神经网络模型和方法，建立四川北部山区输电线路工程投资估算模型，能简便准确地进行可研投资估算，效果很好。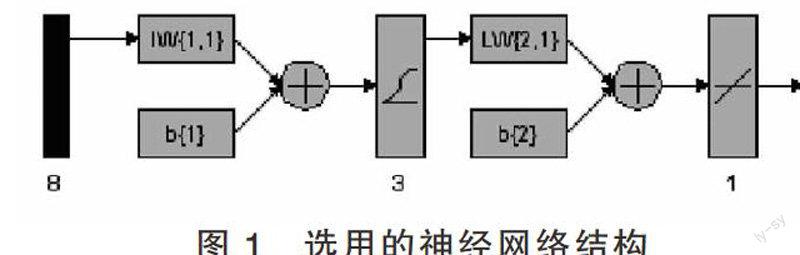

二、问题提出和解决思路

位于四川北部山区的G地级市，市国网公司从实际工作需要和上级要求出发，希望其投资发展部门在无技经和造价人员支持情况下，在编制可行性研究报告时能够由投资发展部门独立给出电力工程投资估算。为此，需要建立一无需掌握过多技术细节、容易理解的估算模型，进行输电线路工程的可研投资估算研究。

问题的解决，关键是投资估算方法和模型的选取建立。

神经网络是一种大规模并行的非线性动力学系统。BP（Back Propagation，后向）神经网络其层与层之间权重可自修正，并已经证明在闭区间内任何一个N维到M维的连续函数都可以用含有一个隐层的神经网络来实现任意精度的逼近。这种非线性、自学习的特点，非常适合输电线路工程的投资估算的预测。

模型确立后，重要的是影响因素即输入变量的选择以及输入数据的处理。

三、因素选择和数据预处理

影响线路工程投资估算的因素很多。选择时既考虑其影响性质和程度，又考虑数据的可取得性，并要结合模型而取舍。下面是选定的影响因素。

电压等级、线路长度、导线截面、环境因素、PPI、CPI、G市就业人员年均工资。

其中电压等级、线路长度、导线截面直接从项目可研批复获得。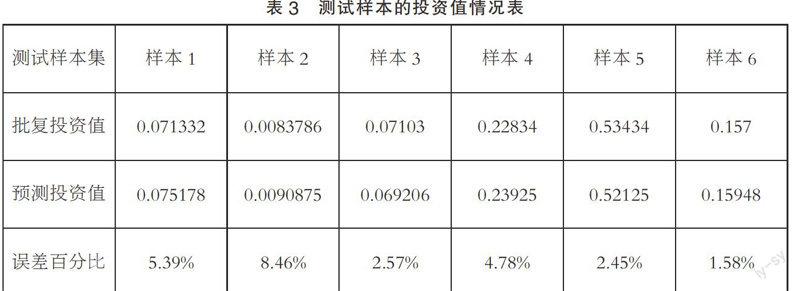

选择工程所在年份的年平均工资、PPI、CPI，是作为投资的动态影响因素，其中G市就业人员年均工资 来源于四川统计局数据，PPI、CPI来源于国家统计局数据。

环境因素是影响因素中最复杂多变的，它包含了气候水文地质地形等，由于其复杂多变，致使其影响程度不易简单测算获得。又由于环境因素对线路工程影响显著不可忽略，模型又提供给投资发展部门（不关注更多技术细节）独立给出电力工程投资估算。论文中为解决这一问题，采用多人评分法。由多名国网G市公司熟悉G市环境和线路工程的人员，比如投资发展部负责前期可研的人员，对各输电线路工程的环境影响投资的程度进行综合打分，取其平均值。从而解决此问题。

具体是由评分人员依据自己的了解和经验，假定其他因素固定，对地质地形气候等环境因素导致输电线路工程费用增大的程度，给所有线路工程项目逐一进行打分，打分标准如下表1所示。

通过对G市供电公司所收集的所有可研批复进行逐一梳理，对线路工程投资估算模型输入变量进行选定和预处理如下表2所示。

输出变量1个，为上级可研批复中批复的工程投资值，单位万元。

收集到的所有有效样本为76个。将所有样本分为训练样本集和测试样本集，从35kv、110kv、220kv线路工程中各选2个共6个样本为测试样本集，其余70个样本为训练样本集。训练样本集用于训练神经网络，测试样本集用于模拟实际情况测试模型。

四、 神经网络模型结构

选用 MATLAB 7.1为研究工具。

神经网络如图1所示，选择三层BP网络，分别为输入层、隐单元层、输出层。

输入层节点I=（I1，I2，......，I9），共9个，其中8个节点（I1，I2，......，I8）对应表2中8个变量，另外一个节点对应阈值。输入变量值在作为网络输入时进行规一化处理成[0，1]范围内值。

规一化公式为，max{I}、min{I}是第j项变量I在76个样本中的最大值、最小值。

中间一层隐单元层，隐单元层中的节点个数选择4个，其中3个节点接受输入层的结果，另外一个节点对应隐单元的阈值。

输出层节点数为1，对应输出变量。

隐单元层采用logsig函数，输出层用purelin函数。网络初始权值在 [-1，1]内随机产生。

五、模型训练

为提高训练效率，选用批处理训练，训练算法选用trainlm方法（Levenberg-Marquardt方法），性能函数选用MSE（mean squared error，均方误差）。

用预处理并规一化了的70条训练样本进行批处理训练，结果显示，在20周期后基本收敛稳定，性能函数MSE已经非常小。如图2所示。

至此，模型训练完成。

六、模型测试

以此训练后的神经网络模型对测试样本集的6条数据进行检验。

测试得到每条样本数据预测投资值和批复投资值（皆为规一化的数据）见表3所示。6个样本的误差百分比的均值为4.21%。模型预测效果良好。

七、结论及展望

神经网络的非线性、自学习的特点，适合输电线路工程的投资估算预测。用此建立的这个模型，无需掌握过多技术细节、无需技经和造价人员支持，适合于国网供电公司投资发展部（或投资决策部）在编制可行性研究报告时独立地较准确给出输电线路工程投资估算。由于模型采用G地级市电网数据训练，论文所建立的模型适合于G地级市以及四川北部山区的国网输电线路工程。

这种方法可以推广应用到其他地区和其他工程的投资估算。

参考文献：

[1]徐武明，徐玖平. 大型工程建设项目组织综合集成模式[J]. 管理学报，2012（01）.

[2] 彭光金，俞集辉，崔荣，韦俊涛，司海涛，朱辉.基于数据挖掘技术的输电工程造价估算[J].工业工程与管理， 2009（03）.

[3] 谢伟群.关于送电线路设计和工程造价的探讨[J].广东输电与变电技术，2005（02）.

[4]徐武明，徐玖平. 大型工程项目勘察承包商选择体系的构建[J]. 软科学，2011（12）.

[5] 胡志根.基于模糊预测的工程造价估算模型研究[J].系统工程理论与实践，1997（02）.

[6]徐武明，徐玖平.大型工程项目监理承包商的选择方法研究[J].统计与决策，2011（19）.