中考数学压轴题分层次教学

杨通明

摘 要：在我省的中考数学科目中，压轴题往往是最难的，也是最考验学生真实水平的，它的设置往往是为了考验学生对于数学知识的综合运用能力。笔者认为，应当针对压轴题进行分层次的教学，不仅彰显教师水平，同时还能够提升学生成绩。

关键词：贵州省；中考数学；分层次教学；压轴题

笔者在对黔南州的中考数学进行了常年的研究与分析，并且在一线的教学当中加以实践，取得了良好的实际教学效果。在这里给各位教师以及同学们进行经验的分享。

一、做好心理攻坚战

数学的考试时间往往比较紧张，很多同学做到压轴题时往往已经所剩无几。这时候如果没有良好的心态，就连题目都会读不懂，更不要说将题目完美解出并拿分了。尤其是结合黔南州的具体出题方式，更是强调灵活性的解题方法。所以，各位教师一定要从心理上对学生予以指导，告诉他们压轴题并不难，其设置的目的也并非为了考倒学生，而是为了考察学生对于数学知识掌握的灵活程度。

通常压轴题分为三部分。第一部分根据已知条件求得问题和第二部分根据已知条件采取逆向思维的能力梳理整道题的脉络求得答案，一般中等数学水平的同学都能答的出；第三部分就是真正意义上的“压轴题”，在做这一题时，千万不能慌，可以根据已知条件和所求问题再重新进行思索，采取多种思路，看看是否存在别的方法和解题方式。

二、重视解题技巧，提升分析能力

仅仅教会学生一道题的作用是相当有限的，但是如果能够教会学生一种解题的思路和解题的技巧，则对于学生的学习来说就非常有益处了。比如在平面几何中，已知条件是AB是圆O的直径，那么学生马上就应当根据这个条件联想到“AB所对应圆周角是直角”，跟这个条件往往会成为解题的关键所在；再比如说，如果要求证明CD是圆O的切线，则需要证明CD与圆O相交于点C，则需要连接OC，并找出OC⊥CD成立。在实际的教学当中，需要经常锻炼学生的这种双向思维的习惯。一旦学生能够拓展开自己的思维，则在解压轴题的时候定会有新的思路和想法。

笔者在实际教学当中总结出了几种常见的解题策略：

1.树立随时随地建立坐标系的思想，懂得数形结合；

2.以直线或者抛物线的知识作为载体，利用函数与方程的思想进行解题；

3.懂得不同知识点之间的融会贯通，擅长利用等价转换；

4.注意某些条件线的平移、旋转和延长，往往通过对已知条件里的直线进行平移或者是延长，就能够得到解题的关键所在。黔南州数学界流传一句话：“遇中点，必延长”。由此可见，一定要注意挖掘潜在的已知条件。

三、案例分析

下面，笔者以黔南州2015年刚刚考过的一道压轴题为例，讲述其解题思路和解题技巧。

本题所占分值为10分，是2015年中考数学的第22题。

1.题目

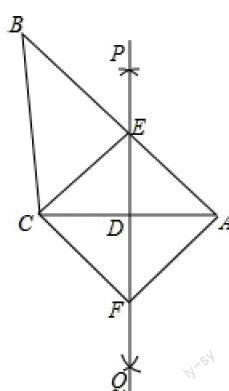
如图所示，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF。

（1）求证：△AED≌△CFD；

（2）求证：四边形AECF是菱形.

（3）若AD=3，AE=5，则菱形AECF的面积是多少？

2.考点

菱形的判定；全等三角形的判定与性质；线段垂直平分线的性质。

3.分析

下面是笔者做出的分析：

（1）由作图知：PQ为线段AC的垂直平分线，从而得到AE=CE，AD=CD，然后根据CF∥AB得到∠EAC=∠FCA，∠CFD=∠AED，利用ASA证得两三角形全等即可；

（2）根据全等得到AE=CF，然后根据EF为线段AC的垂直平分线，得到EC=EA，FC=FA，从而得到EC=EA=FC=FA，利用四边相等的四边形是菱形判定四边形AECF为菱形.

4.解答过程

解：（1）由作图知：PQ为线段AC的垂直平分线，∴AE=CE，AD=CD

∵CF∥AB，∴∠EAC=∠FCA，∠CFD=∠AED

在△AED与△CFD中，∠EAC=∠FCA，∠CFD=∠AED，且AD=CD

∴△AED≌△CFD

（2）∵△AED≌△CFD，∴AE=CF

∵EF为线段AC的垂直平分线，∴EC=EA，FC=FA

∴EC=EA=FC=FA

∴四边形AECF为菱形

（3）∵AD=3，AE=5，∴根据勾股定理得：ED=4

∴EF=8，AC=6，∴S菱形AECF=8×6÷2=24

∴菱形AECF的面积是24

5.点评与分析

本题考查了菱形的判定、全等的判定与性质及基本作图，解题的关键是了解通过作图能得到直线的垂直平分线。这就牵扯到了笔者在前文2.4当中所讲到的，通过作图的方式，将已知条件进行延伸，从而找出隐藏的已知条件，方便进一步的解题。

四、注意答题规范

平时教学注重认真审题，探究解题思路，得出正确答案，同时注意答题规范，板书演示，详略得当。提醒学生答题时关键不能省，过程不过繁，书写要整洁，布局要合理。

五、结束语

压轴题是为了让参加中考的学生成绩更有区分度，因此并非所有学生都能够答上压轴题。但是我们要知道中考的评分标准是只要写上了相关知识点就能够给分，因此即使无法得到满分，也应当尽力拿分。

参考文献：

[1]李振盛.中考数学压轴题分层次教学[J].亚太教育，2016（5）：167-168.

[2]付艳艳.浅谈中考数学复习中应注意的问题[J].商情，2014（39）：205.

（作者单位：贵州省黔南州惠水县民族中学）