基于CW环氧浆液流变性的注浆扩散理论研究
邓弘扬,汪在芹,魏 涛
(1. 长江科学院 a.材料与结构研究所; b.院长办公室,武汉 430010;2. 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌 443002)
基于CW环氧浆液流变性的注浆扩散理论研究
邓弘扬1a,2,汪在芹1b,2,魏涛1a,2
(1. 长江科学院 a.材料与结构研究所; b.院长办公室,武汉430010;2. 三峡地区地质灾害与生态环境湖北省协同创新中心,湖北 宜昌443002)
摘要:为建立更符合实际的化学注浆扩散模型,针对CW环氧浆液的流变性能进行了多组黏度时变性试验研究,结果表明温度不变时各种配比浆液的黏度和时间存在一定的指数函数关系。结合球形、柱形注浆扩散理论,对环氧浆液的注浆量和注浆扩散半径公式进行了时变性优化。通过分析优化公式,显示环氧浆液在渗透过程中呈减速运动;当各种环境系数保持不变时,注浆最大注浆量和最大扩散半径取决于黏度与时间函数关系中参数的乘积。对比了各组环氧浆液的函数参数乘积,得到黏度增长较慢的浆液具有更好的注浆扩散能力。
关键词:CW环氧浆液;流变性;黏度;注浆量;注浆扩散半径
1研究背景
目前,化学注浆已经广泛应用于渗透注浆工程中,相较水泥浆,对化学浆的研究尚无完整的理论体系。国内外工程中计算浆液的注浆量和注浆扩散半径广泛地依据渗透理论[1-2],该理论对实际注浆有一定的指导意义,也存在一定的局限性,如没有考虑浆液流变性中黏度的时变性。若进一步研究化学浆液的流变性能,建立更符合实际的化学注浆扩散模型,描述化学浆液在被灌介质中的运动规律并预测出浆液的注浆扩散范围,不仅能减小注浆的盲目性,更能提高注浆效率和效益,具有很大的理论意义和实践价值。为此,本文基于已经成功应用于工程实际的CW环氧浆液对其流变参数中黏度的时变性进行试验研究,并将结果补充进注浆扩散理论作进一步分析探讨。
2环氧浆液流变性
要建立注浆扩散模型,首先必须确定浆液的流型,前人证明了在注浆液流型不变的假设后,方可对浆液的流变性能和扩散规律进行研究[3-4]。很多学者认为化学浆液在其具有注浆性能时属于牛顿流体[5],流变参数对浆液的扩散半径有着较大的影响,而黏度是影响注浆液流变性能的最主要参数[6],我们通常采用黏度来反映注浆液的流变性能。前人总结的注浆扩散理论大多忽视了浆液黏度随时间的变化以简化扩散模型,那么研究浆液流变性中黏度的时变性,可以对现有理论进行更贴合实际的补充。
2.1CW环氧浆液黏度时变性试验
按质量比m(A)∶m(B512)=4∶1,5∶1,6∶1和m(A)∶m(B511)= 4∶1,5∶1,6∶1配制CW环氧浆液(A,B512和B511分别为CW环氧浆液A组分、快固化剂和慢固化剂),快速搅拌使其充分反应;将搅拌后的浆液倒入NDJ-79型旋转黏度计的测量筒中,筒外通恒定室温的流水保持筒内温度不改变,测量浆液的黏度,记录黏度初值,并记录当时的温度;保持测试环境温度不变,每隔一段时间记录3次黏度值,取平均值后作为可用数据,直到黏度值>200 mPa·s后即可停止记录[7-8]。
采用OriginLab作图并对得到的6组数据进行分析拟合,得出不同组分、不同配比环氧浆液的黏度与时间函数关系,绘制拟合关系曲线,如图1所示。
通过软件拟合可知各组CW环氧浆液的黏度η随时间t变化均符合形如η=aebt的指数函数关系,其中参数a表示浆液的初始黏度,参数b表示浆液黏度增长的快慢程度,b值越小,黏度增长越慢。a,b取值以及拟合系数R2值如表1所示。

图1 环氧浆液黏度与时间拟合关系曲线

浆液名称配比abR2A+B512A+B5114∶128.6480.03290.99735∶126.3870.01570.99826∶124.3130.00770.99854∶122.5620.00510.99715∶120.5730.00270.99796∶118.5440.00250.9968
从表1不难看出6组浆液的拟合系数R2均大于0.995 0,非常接近于1,可见CW环氧浆液的黏度随时间变化规律确实符合η=aebt的指数函数关系,说明温度不变条件下CW环氧浆液在其具有注浆性能时的黏度存在时变性。
对比表1中不同配比及组成浆液的待定系数a,b值可以发现:a从物理意义上代表了化学浆液的初始黏度,其值从28.648减小到18.544,虽慢固化剂浆液的黏度比快固化剂的更小,A组分加入量越多,初始黏度则越低,但数值上差距不大。这是因为浆液在记录初值的时刻点近似于牛顿流体,浆液组分间的交联反应还没来得及促使浆液的黏度显著升高,所以a值相近;而b值从0.032 9减小到0.002 5,降低了13倍有余,其物理意义代表了化学浆液黏度随时间增长的快慢程度,b值越大则黏度上升越快,反之则越慢,这恰恰说明了随着环氧基团与其他基团交联反应的进行,浆液中聚合成大分子量的分子会慢慢增多,加入慢固化剂的浆液其黏度对比加入快固化剂的浆液(简称“快浆”)增长便会更慢,而A组分加入量越多则浆液黏度增长就越缓慢。
2.2注浆扩散理论
1938年马格作了如下假定:①被灌土体为均质各向同性体;②浆液为牛顿体;③浆液从钻杆底部孔灌入土体,注浆源为点源,浆液在地层中呈球状扩散[9-10],如图2所示。
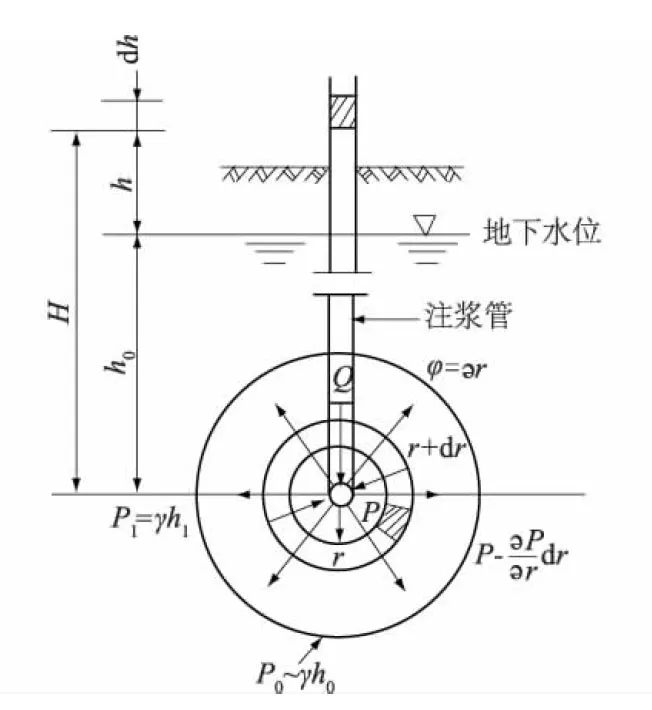
图2 球形理论注浆扩散示意Fig.2 Schematic diagram of spherical diffusion
根据达西定律和边界条件[11],最后推导出形式简单的球形扩散公式为
(1)
式中:Q为浆液的流量(cm3/s);r1为浆液渗透半径(cm);k为土体的渗透系数(cm/s);β为浆液黏度与水的黏度之比,β=ηg/ηw,其中ηg,ηw分别为浆液和水的黏度;h0为注浆点静水压力水头(cm);H为注浆点总压力水头(cm);t为注浆时间(s);r0为注浆管的半径(cm)。
将式(1)移项变换,并将β用浆液黏度与水的黏度之比代换,再将上述试验得到的CW浆液黏度随时间变化的关系式η=aebt代入式中可得
(2)
人们以往只考虑初始黏度作为黏度的唯一指标,而式(2)对比原马格公式考虑了化学浆液黏度随时间的变化,更加准确地反映了化学浆液任意时刻的扩散量。
化学浆液在被灌体里渗透时,考虑r1>>r0时可得浆液的球形扩散半径r1最终表达式为
(3)
式中n为土体的孔隙率。
将浆液黏度随时间的变化规律η=aebt引入式(3)中,同理变换简化可得
(4)
得到的式(4)即为考虑了浆液黏度随时间变化的化学浆液球形扩散半径公式优化形式,它更加准确地表明了化学浆液任意时刻t的扩散范围。
对式(4)作一定的变换化简为如下形式,引入c作为与浆液本身性质无关的常数,此常数只与被灌体、注浆孔、水的黏度和注浆压力等环境系数有关,则可得
(5)
浆液的扩散半径r1与注浆时间t有一定的函数关系,记为F(t),则有
(6)
将式(6)左右两边对时间t求导,整理后可得
(7)
令F′(t)=0得到1-bt=0,即t=1/b。当t<1/b时,F′(t)>0;当t>1/b时,F′(t)<0。根据F′(t)所代表的物理意义,可知其为化学浆液的球形扩散速度,不能为负数,说明t的取值范围只能在0~1/b之间。以此推出化学浆液的最大球形扩散半径为
(8)
当浆液达到最大扩散半径时最大注浆量为
(9)
再将表示化学浆液扩散速度的函数F′(t)表达式(式(7))左右两边同时对时间t求导,整理后即能得到物理意义为化学浆液球形扩散加速度的函数F″(t),形式为
(10)
观察式(10)可知,当t在0~1/b的范围内取值时,F″(t)<0,表明化学浆液在被灌体里球形渗透直到停止的过程中加速度一直保持负值,即浆液在渗透时作减速运动。
由上述试验研究可知,化学浆液的黏度随时间的增大而升高,既然浆液在渗透时作减速运动,则浆液的扩散速度随其黏度的增大而降低,而当浆液黏度过大时,浆液的减速使其扩散速度就会在很短距离内降低到0,注浆扩散停止。
柱形扩散与球形扩散的假设一致[12],区别只在于浆液在压力作用下于孔下部呈柱形扩散,如图3所示。

图3 柱形理论注浆扩散示意Fig.3 Schematic diagram of cylindrical diffusion
同理可以得出浆液的柱形扩散半径r2表达式为
(11)
将浆液黏度随时间的变化规律η=aebt引入式(11)中,按照上述方法进行类似变换可得考虑浆液黏度随时间变化的柱形扩散半径公式优化形式,其表达式为
(12)
对式(12)作一定的变换化简为如下形式,引入m为与浆液本身性质无关的常数,类似于上述常数c,则有
(13)
可见式(13)为隐函数形式,对比球形扩散推导中对(1/r0-1/r1)作出简化,最后得到r1的显函数关系式而言误差更小。将式(13)左右两边对时间t求导,整理后可得
(14)
观察式(14)后可以得到与球形扩散一致的结论:当t=1/b时,r2的一阶导数等于0,即柱形扩散速度等于0。类似地得到t的取值范围只能在0~1/b之间。以此可推出浆液的柱形最大扩散半径为
(15)
再将柱形扩散速度表达式左右两边同时对时间t求导得到加速度表达式,形式比较复杂,在此不作表述,计算后也可以得到t在0~1/b的范围内取值时,r2的二阶导数<0,表明浆液在被灌土体里柱形渗透直到停止的过程中加速度一直保持负值,同样说明浆液渗透时作减速运动,与球形扩散推导时得到的结论一致。
依据以上球形扩散和柱形扩散的公式不难发现,当所有与浆液本身性质无关的环境待定系数保持不变时,环氧浆液的最大注浆量和最大扩散半径均与黏度时间函数η=aebt中参数a,b的乘积有关。根据试验结果表1中的数据计算得知,a,b乘积随着A组分量的增加、B组分从快固化剂改为慢固化剂而减小,如图4所示。

图4 不同浆液的a,b乘积Fig.4 Product of a and b of different slurries
综合2种注浆方式的优化表达式(8)、式(15)和图4中a,b的乘积推知:
(1) 由于注浆扩散表达式中a,b乘积为分母项,其值越小说明扩散半径和扩散量越大;又根据前述分析知各组浆液的初始黏度相差不大,则黏度增长更慢的浆液比快浆扩散距离长,注浆量大,其中m(A)∶m(B512)=4∶1浆液的a,b乘积是m(A)∶m(B511)=6∶1浆液的20多倍,差距很大。
(2) 同种组分浆液中A组分量越大,扩散距离越大,注浆量也越大,其中m(A)∶m(B511)=4∶1浆液的a,b乘积为m(A)∶m(B511)=6∶1浆液的2倍多。
上述试验结果及推导说明了黏度增长更慢的浆液比快浆更能渗透到被灌体中,拥有更好的渗透性,且多种浆液进行复合注浆渗透时,采用先快浆后慢浆的注浆办法也与应用CW环氧浆液的实际工程项目中的经验和效果相符合,验证了该理论的正确性。
3结论
针对CW环氧浆液的流变性能进行了多组不同组分、配比浆液的黏度时变性试验研究,得到如下结论:
(1) 温度不变时各组浆液的黏度随时间变化规律符合η=aebt的指数函数关系。
(2) 将黏度与时间的指数关系η=aebt应用于球形扩散理论和柱形扩散理论中,得到了考虑浆液黏度随时间变化的注浆量和扩散半径表达式优化形式。
(3) 推导分析所得优化公式,指出浆液在被灌介质中的渗透过程呈减速运动,注浆的最大注浆量和最大扩散半径在与浆液本身性质无关的环境系数保持不变时,只与浆液的黏度时间函数中参数a,b的乘积有关,乘积越小,最大扩散半径和最大注浆量越大。
(4) 对比不同组分、配比的6组CW环氧浆液,得到黏度增长更慢的浆液比快浆具有更好的注浆扩散能力。
参考文献:
[1]BAKER C. Comments on Paper “Rock Stabilization in Rock Mechanics”[R]. New York: Springer-Verlag, 1974:45-78.
[2]顾慰慈. 渗流计算原理及应用[M]. 北京:中国建材工业出版社, 2000:25-33.
[3]莫乃榕. 工程流体力学[M]. 武汉:华中科技大学出版社, 2000:76-83.
[4]YESILNACAR M I.Grouting Applications in the Sanliurfa Tunnels of GAP, Turkey[J]. Tunnelling and Underground Space Technology, 2003, (18):321-330.
[5]SNUPAREK R,SOUCEK K.Laboratory Testing of Chemical Grouts[J]. Tunneling and Underground Space and Technology, 2000, 15(2):175-185.
[6]杨秀竹,王星华,雷金山. 宾汉体浆液扩散半径的研究及应用[J]. 水利学报, 2004, 35(6): 75-79.
[7]汪在芹,魏涛,李珍,等. CW系环氧树脂化学灌浆材料的研究及应用[J]. 长江科学院院报, 2011,28(10):167-170.
[8]魏涛,汪在芹,薛希亮,等. CW系化学灌浆材料的研制[J]. 长江科学院院报, 2000, 17(6): 29-31.
[9]阮文军. 基于浆液粘度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报, 2005, 24(15): 2709-2714.
[10]阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报, 2005, 27(1): 69-73.
[11]坪井直道. 化学注浆法的实际应用[M].吴永宽,译. 北京:煤炭工业出版社, 1980.
[12]刘嘉财,王保昌,崔文广,等. 水工聚氨酯灌浆[C]//水利电力科学研究院科学研究论文集(第8集). 北京:水利水电出版社,1982:169-176.
(编辑:黄玲)
Grout Diffusion Theory Based on CW Epoxy Grout’sTime-varying Characteristics of Viscosity
DENG Hong-yang1,3, WANG Zai-qin2,3, WEI Tao1,3
(1.Material and Engineering Structure Department, Yangtze River Scientific Research Institute, Wuhan430010, China; 2.Administration Office, Yangtze River Scientific Research Institute, Wuhan430010, China; 3.Collaborative Innovation Center for Geo-hazards and Eco-environment in Three Gorges Area of Hubei Province, Yichang443002, China)
Abstract:In order to explore the model of chemical grout diffusion which is more consistent with reality, we conducted tests on the time-varying characteristics of viscosity of CW epoxy grout, and obtained that the relationship between viscosity and time at a given temperature accords with exponential function. Furthermore, according to the spherical diffusion theory and the cylindrical diffusion theory, we optimized the formulas of epoxy grout quantity and grout diffusion radius in terms of time-varying characteristics. The optimized formulas reveal that the grout is in negative acceleration motion in the process of infiltration; the maximum grout diffusion radius and maximum grout quantity are dependent on the product of the parameters of viscosity-time function when other parameters which don’t depend on grout itself remain constant. Through comparison of the product of function parameters of different epoxy slurries, we conclude that the grout of which viscosity grows more slowly has better penetration.
Key words:CW epoxy grouting slurry; time-varying characteristics; viscosity; grout quantity; grout diffusion radius
中图分类号:TV543.2
文献标志码:A
文章编号:1001-5485(2016)05-0121-04
doi:10.11988/ckyyb.201501902016,33(05):121-124,134
作者简介:邓弘扬(1990-),男,湖北武汉人,助理工程师,硕士,主要从事化学灌浆新材料的研发与水工工程安全方面的研究,(电话)15972972302(电子信箱)404026767@qq.com。
基金项目:国家自然科学基金项目(51378078)
收稿日期:2015-03-16;修回日期:2015-05-21

