基于不规则颗粒离散元的土石混合体三维随机模型及其数值试验
金 磊,曾亚武,叶 阳,夏 磊
(武汉大学 土木建筑工程学院,武汉 430072)
基于不规则颗粒离散元的土石混合体三维随机模型及其数值试验
金磊,曾亚武,叶阳,夏磊
(武汉大学 土木建筑工程学院,武汉430072)
摘要:为了更加真实地模拟土石混合体的物理力学特性,提出了一种基于不规则块石球度和凹凸度的随机几何模型生成技术,并建立了相应的块石三维离散元模型。然后采用无底圆筒堆积试验对球度和凹凸度这2个块石几何模型控制参数进行了数值验证。最后建立了符合宏观统计规律的土石混合体三维离散元随机模型,对土石混合体大三轴试验进行颗粒流模拟,并与室内试验结果进行对比分析。结果表明:所提出的不规则块石几何模型随机生成方法简单实用,几何模型控制参数合理有效;通过选取合适的颗粒细观参数,建立基于随机不规则块石体的土石混合体数值模型,能很好地模拟土石混合体的物理力学性质,包括颗粒之间的细观接触特征、土石混合体的应力-应变关系特征等,为进一步研究土石混合体的变形破坏机理提供了一条有效的途径。
关键词:土石混合体;不规则颗粒;三维离散元;无底圆筒堆积试验;大三轴试验
1研究背景
土石混合体(soil-rock mixture,SRM)是指第四纪以来形成的,由具有一定工程尺度、强度较高的块石、细粒土体及孔隙构成且具有一定含石量(rock block proportion,RBP)的极端不均匀松散岩土介质系统[1]。土石混合体在自然界中分布非常广泛,地球上绝大多数滑坡体都是由土石混合体构成,研究土石混合体变形破坏机理对于进一步深化土石混合体力学理论体系和防治滑坡等地质灾害具有重要的意义。
有关土石混合体的研究主要包括土石混合体原位地质调查[2-3]、大型原位试验[4-5]、室内试验[6-7]和数值模拟[8-10]。原位地质调查可以获得土石混合体的分布、成因等资料,但无法揭示土石混合体的受力变形特征;原位试验和室内试验可以从宏观上揭示土石混合体的受力变形特征,但试验结果由于抽样的关系存在较大的离散性,也很难揭示其变形破坏机理。数值模拟大体上分为2类:一类是将土石混合体视为连续介质,采用连续介质的数值模拟方法,如利用有限元法、有限差分法等开展的研究;另一类是基于离散介质的数值模拟方法。由于土石混合体具有典型的非均质和非连续性,采用传统的建立在宏观连续介质上的力学模型和相应的分析方法,难以合理描述和反映其内部结构的复杂性,也难以从细观水平上揭示其变形破坏机理。而基于离散介质的数值模拟方法,如颗粒离散元方法,假设岩土体由颗粒组成来研究其宏观与细观力学特征,这类方法在分析非连续、大变形、各项异性力学特征方面具有一定优势,已被越来越多的学者所采用,且这类方法的关键在于能够建立反映实际土石混合体细观结构特征的数值模型。
徐文杰等[1]开发了基于任意多边形及椭圆形块石的土石混合体细观结构随机生成技术,并基于有限元法研究了含石量、块石空间分布和土-石界面类型等对土石混合体强度和破坏特征的影响,取得了一些有意义的研究成果。油新华[2]将块石简化为规则几何形状(如圆形、三角形等),建立了土石混合体的随机细观结构模型,并基于有限差分法研究了含石量和块石形状等对土石混合体强度和破坏特征的影响。丁秀丽等[10]基于数字图像处理技术获得了土石混合体典型剖面图像,建立了土石混合体颗粒流平面模型并进行了双轴压缩试验的数值模拟。上述研究, 即建立的块石模型都是平面模型,难以反映土石混合体的三维力学特征,此外将块石体简化为相对规则的形状,与实际块石形状存在较大的差异,即使是基于数字图像处理技术建立的块石模型也存在一定的局限性,难以获取所有研究区域的数字图像,也很难找到为某种研究目的所需要的理想剖面等。因此,尽管采用离散元方法开展土石混合体变形破坏机理的研究是一条有效的途径,但针对土石混合体数值模型建立方法的研究尚需深入进行,只有建立能够反映土石混合体工程实际的三维数值模型,尤其是不规则块石的三维数值模型,才能获得有意义的研究成果。
杜欣等[11]介绍了一种基于CT扫描的不规则颗粒三维离散元建模技术,能够获得不同精度的不规则颗粒三维离散元模型,使得模型精度与所需基本球体数目之间达到平衡,是一种有效的不规则颗粒建模方法。但是,对于土石混合体中存在的大量不规则块石,很难逐一进行CT扫描,而根据块石形态的统计特征建立符合宏观统计规律的块石随机结构模型则能较好地解决上述问题。为此,本文首先提出一种基于统计规律的不规则块石几何模型随机生成技术,并基于文献[11]提出的不规则颗粒三维离散元建模技术建立了不规则块石的三维离散元模型,并采用无底圆筒堆积试验验证不规则块石随机几何模型控制参数的有效性;同时通过分别建立块石形状为球体和随机不规则块体的土石混合体大三轴数值模型,开展了数值模拟试验,并与室内大三轴试验结果进行比较,以此验证本文提出的基于不规则颗粒离散元的土石混合体三维随机模型的合理性。
2不规则块石建模
土石混合体中块石颗粒形状和大小在一定程度上反映了其历史形成过程,土石混合体的宏观力学行为取决于细观水平上颗粒之间的相互作用,而颗粒形状是影响颗粒间相互作用的一个非常重要的因素。已有颗粒材料的研究结果表明:颗粒形状越不规则,自然堆积状态下孔隙比越大、整体刚度越小、临界摩擦角越大、对应力状态的变化越敏感[12]。油新华[2]和A. Graziani等[3]的研究也表明土石混合体中块石体的形态对其物理力学特性有着重要的影响。因此,要准确模拟土石混合体的力学性质和运动特性,必须首先实现不规则块石的模拟。
2.1不规则块石随机几何模型
对不规则颗粒的模拟首先需要对颗粒形态进行恰当的描述。部分学者采用分形理论或傅里叶分析方法来进行描述,如Bangaru等[13]将块石的二维外轮廓曲线采用快速傅里叶变换分解成一系列不同空间频率的正弦曲线来进行描述,不过这种方法数学计算过程复杂,不利于推广和应用。另外一些学者提出对不规则颗粒形态的描述可以分3个尺度来进行:①颗粒尺寸尺度上的,可以定义为球度,它反映了颗粒的总体形状,表示颗粒三向尺寸(长、宽、高)之间的比例;②比颗粒尺寸小一个数量级尺度上的,可以定义为凹凸度,它反映了颗粒表面的宏观凹凸程度;③细观尺度上的颗粒表面的粗糙度[12]。孔亮等[14-15]从受力和变形机理角度分析认为:颗粒之间的宏观内摩擦角是颗粒抗滑动与翻滚能力的体现,其中颗粒抗转动能力受颗粒的球度支配;颗粒间的宏观嵌入咬合力受颗粒外形的凹凸度支配;颗粒接触面、点之间的微观咬合受颗粒细观摩擦因数支配。
目前对随机形状块石的模拟多见于混凝土中粗骨料的研究,已有的建模方法基本上可分为以下2种:①通过将随机生成的三角形或多边形或具有简单数学表达的曲面作为基础,然后按特定算法进行延拓生成骨料,并通过凹凸判断来控制骨料为凸形,最后通过冲突判断来实现骨料的无重叠投放[16];②将基本几何体用多个平面进行随机切割来获得随机多面体模型[17]。已有的这些随机块体建模方法算法都比较复杂,效率都不高,很难生成高含石量的土石混合体模型,而且随机块体都是凸体,而实际的土石混合体滑坡中的块石体表现更多的是凹凸并存,因此,有必要提出一种新的适用于模拟土石混合体中块石形态特征的建模方法。
为了方便实际中对不规则块石形态特征进行描述和统计以建立符合宏观统计规律的块石模型,以及将块石的形态特征和受力变形机理联系起来,本文采用上述的球度、凹凸度作为块石几何建模的控制参数,提出了一种基于APDL(ANSYS参数化设计语言)参数化建模的随机块石体建模新技术,其主要原理和步骤概述如下。
2.1.1随机球度基面生成
将块石体三向尺寸中最大的作为建模时x向长度,最小的作为建模时z向长度,则z向长度与x向长度之比即为块石的球度S,处于中间的尺寸作为y向长度,即为颗粒的粒径。根据x,y,z向尺寸即可建立一个中心在原点的长方体,删除长方体,保留组成长方体的6个面,即可得到规定球度的基面。
应用时可根据实际统计得到的块石三向尺寸的特征,设定x向、y向长度值变化范围和球度S随机变化范围,由此可得到符合实际统计规律的随机球度的基面。
2.1.2随机凹凸面生成
将第2.1.1节得到的球度基面划分网格,单元形状宜选择三角形壳单元,单元尺寸可根据颗粒表面凹凸点个数确定,如较少(4个左右)则可将各边的分段个数设为1,以此类推。划分网格后记录各三角形面单元的组成节点信息,得到各个节点的球坐标,然后对各节点球坐标中的第一个分量r(该节点到原点的距离)进行随机比例的缩小变换,用公式表示为:

(1)

(2)
式中:a为缩小比例值的下限;RAND(a,1)为a~1范围内的随机数;C为块石表面点的凹凸度。根据前面记录的三角形面单元与其组成节点的关系以及随机变换后的新节点坐标重新生成面,即可得到需要的随机凹凸度的曲面。
2.1.3随机几何模型生成
根据变换后得到的随机曲面围成的空间即可建立随机几何体模型,将单元类型改为四面体单元,对生成的几何体进行体网格划分,即可得到满足后续离散元建模要求的几何模型。
根据已有土石混合体中块石形态特征的统计调查[18]并经试算对比,本文在块石随机模型的生成过程中进行了一定的简化,将块石颗粒y,z向尺寸设为相同,y,z向长度与x向长度比值即球度S设为在0.3~0.8的范围内随机取值,初始随机基面网格划分尺寸设为每个边的分段数均为2,各节点球坐标第一分量缩小比例在0.4~1.0的范围内随机取值,即凹凸度为0.6。在上述参数取值情形下,由第1步得到的某个随机球度的基面(x向长度为40 mm)如图1(a)所示,由第2,3步得到的随机几何模型如图1(b)所示。

图1 典型不规则块石几何模型Fig.1 Establishment for typical geometric model ofirregularly shaped(IRS) rock block
从以上建模方法和结果可以看出,本文提出的以球度和凹凸度作为几何模型控制参数的建模方法简单实用,只需要经过3步操作即可获得不规则块石的随机几何模型。至于不规则颗粒表面的粗糙度,几何模型中暂不用考虑,因为一方面可以通过数值模拟时对颗粒设定不同的细观摩擦因数来表示,另一方面由基本球体填充后建立的离散元数值模型的表面是不平整的,可近似模拟粗糙度。
2.2不规则块石离散元模型及其密度优化
根据第2.1节方法所得到的不规则块石几何模型,基于不规则颗粒三维离散元建模技术[11],可以建立不规则块石的三维离散元模型。其主要步骤归纳如下:
(1) 针对所获得的已划分网格的不规则块石几何模型,导出模型的表面节点坐标和内部节点坐标信息。
(2) 对于任意一个内部节点,计算其到每个表面节点的距离,只记录并存储其中的最小值。对所有内部节点都进行一次计算,即可得到所有内部节点到表面各自对应的最小距离值。然后以内部节点为球心,以对应的最小距离值为半径生成球体,所有的球体组合就能刻画出不规则块石的外形。
(3) 根据研究的需要,引入最小球体半径Rlim和有效空间系数K来对基本填充球体数量进行优化,以节省计算资源。
图1(b)中建立的不规则块石几何模型划分网格后有2 314个表面节点和6 671个内部节点,则初始填充球个数为6 671个,如图2(a)所示,这样生成颗粒集合体时球体数量将会非常多,造成计算效率低下,因此,需要引入控制参数进行优化。取最小球体半径Rlim为2 mm,有效空间系数K为1.10,则优化后的离散元模型如图2(b)所示,该离散元模型由544个球体构成。由图2可见,优化后的模型填充球体数大大减少,而模型形态特征基本相同,可以大大节省计算资源。

图2 典型不规则块石三维离散元模型Fig.2 Typical 3-D DEM model of IRS rock block
基于基本球体重叠构建不规则块石的建模方法,不可避免地会出现模型密度分布不均匀的现象,为此,本文采用平均密度的方法使得模型的质量与实际块石的质量相等,用公式表示为:
(3)
(4)
式中:ρm为优化后各球体赋值密度;Vclump为模型体积;ρ0为颗粒实际密度;Vioverlap为每个球体中重叠的体积。
3不规则块石无底圆筒堆积数值试验
3.1颗粒流数值平台(PFC3D)概述
三维颗粒流数值平台(PFC3D)根据颗粒离散元理论,采用显示差分算法,交替运用力-位移定律和牛顿运动定律来模拟颗粒之间的相互作用和运动过程。PFC3D提供了3种基本的接触模型,分别是接触刚度模型、滑移模型和黏结模型。其中黏结模型分为接触黏结和平行黏结。根据土石混合体的结构组成特征,本文选取接触刚度模型、滑移模型和接触黏结模型来进行模拟。
PFC3D中提供了clump以供不规则颗粒的模拟,它由基本的球体颗粒聚集而成,基本颗粒间位置保持相对固定,在循环过程中基本颗粒间的接触计算被忽略,从而大大节约计算时间。clump边缘颗粒与其外部颗粒产生相互作用,但是不管是否有接触力作用在其上面,clump都不会解体[19]。土石混合体中块石的强度和刚度较细粒土体基质要大得多,因此,采用clump来模拟不规则块石是比较合适的。
3.2 无底圆筒堆积数值试验
3.2.1数值试验方案
无底圆筒堆积试验是散体颗粒材料物理特性的基础试验之一,用于测定颗粒集合体的自然安息角(angle of repose,AOR)。一般来说,对于无黏性颗粒,无底圆筒堆积试验所测得的自然安息角应该等于颗粒系统的内摩擦角,而内摩擦角是散体颗粒材料最主要的物理力学参数之一。为了测试和验证不规则颗粒球度和凹凸度对散体颗粒材料物理力学性质的影响,本节分别进行了各块石体球度和凹凸度单独变化时的块石集合体无底圆筒堆积试验的数值模拟。
为便于比较,数值试验采用当量粒径均为50 mm的块石颗粒,所谓当量粒径是指与该块石体积相同的球体的粒径。采用第2.2节的建模方法建立三维离散元模型时取最小球体半径为2 mm,有效空间系数为1.20,各块石密度均为2 680 kg/m3,法向刚度和切向刚度均为109N/m,细观摩擦因数为0.4。无底圆筒直径为200 mm(4~5倍粒径),颗粒堆积高度为600 mm(3倍圆筒直径),圆筒和地面均用墙来模拟,其刚度和摩擦因数与颗粒相同。为了尽可能真实地模拟无底圆筒堆积试验的环境,本文采用颗粒自由落体填充方法对圆筒模型进行填充,提筒速度设为0.5 mm/s。填充后的试样如图3所示,提筒后的堆积体如图4所示。
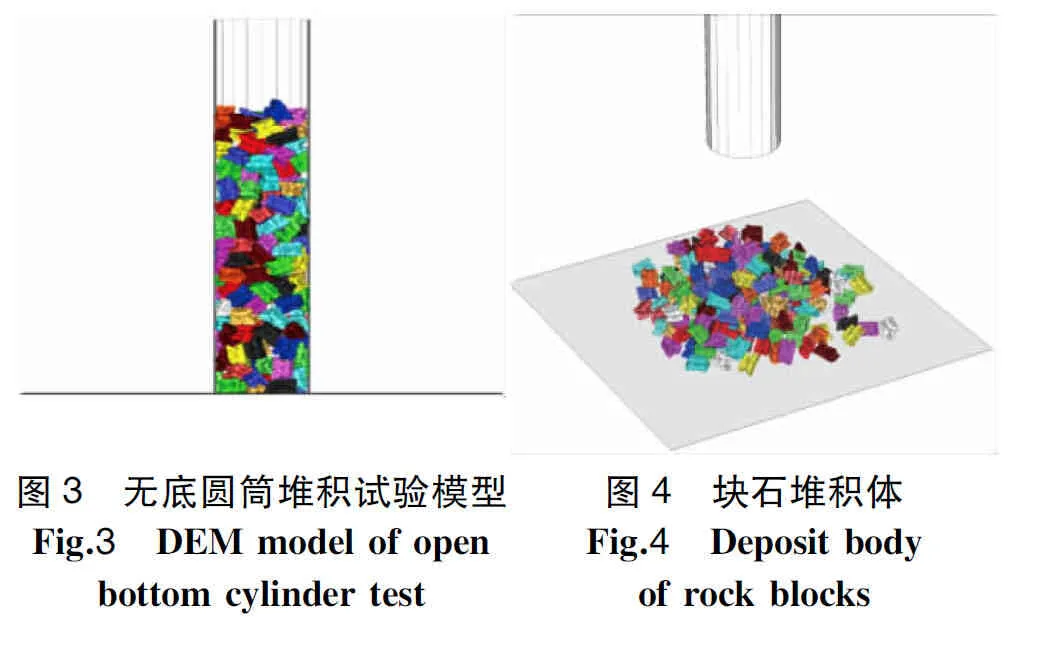
图3 无底圆筒堆积试验模型Fig.3 DEMmodelofopenbottomcylindertest图4 块石堆积体Fig.4 Depositbodyofrockblocks
3.2.2数值试验结果分析
3.2.2.1不同球度块石堆积体的试验结果

图5 不同球度的块石离散元模型Fig.5 DEM models of rock blocks withdifferent sphericity

图6 不同球度块石堆积体形态和自然安息角Fig.6 Morphology and AOR (angle of repose) of depositbody of rock blocks with different sphericity
取块石球度分别为0.9,0.6和0.3,建立相应的块石堆积体模型。此时单个块石表面无凹凸(离散元数值模型表面并非平面,而是由若干基本球体表面构成,可近似描述颗粒表面的粗糙度),即为长方体。3种球度块石的三维离散元模型如图5所示。试验时,当颗粒集合体运动停止时,不同球度块石对应的堆积体形态和自然安息角如图6所示。由图6可见,块石表面无凹凸时,随着块石球度的减小,即颗粒长短轴比逐渐增大,堆积体的自然安息角逐渐增大。3.2.2.2不同凹凸度块石堆积体的试验结果
取块石凹凸度分别为0,0.3和0.6,建立相应的块石堆积体模型。此时各块石的球度保持不变,均为0.6,3种凹凸度块石的三维离散元模型如图7所示。

图7 不同凹凸度的块石离散元模型Fig.7 DEM models of rock blocks withdifferent angularity
需要指出的是,为了保证各凹凸度块石之间具有明显的差别以便进行对比,这里在建立几何模型的第2步时,各节点的内缩比例并没有在设定的范围内随机取值,而是按照线性规律变化,即初始球度的基面划分网格后,第一个节点的缩小比例为1(不内缩),最后一个节点的缩小比例分别为1,0.7和0.4,其它节点的缩小比例按编号线性插值得到(近似均匀分布)。试验时,当颗粒集合体运动停止时,不同凹凸度块石对应的堆积体形态和自然安息角如图8所示。由图8可见,相同球度条件下,随着块石凹凸度的增大,即颗粒表面凹凸程度逐渐增大,堆积体的自然安息角也随之增大。

图8 不同凹凸度块石的堆积体形态和自然安息角Fig.8 Morphology and AOR of deposit body of rockblocks with different angularity
不同球度和凹凸度的块石集合体无底圆筒堆积数值试验结果表明,块石球度越小、凹凸度越大,块石体形态越不规则,其堆积体的自然安息角越大,即松散堆积体的内摩擦角越大,这与已有研究结果[12]是一致的。由此可见,本文用于描述块石体不规则特征的2个控制指标(球度和凹凸度)不仅能够很好地描述块石的不规则形态,而且能够很好地体现不规则块石的受力变形特性,说明本文所提出的不规则颗粒几何模型建模方法控制参数是合理和有效的。
4土石混合体大三轴试验数值模拟
4.1土石混合体室内大三轴试验
截至目前,专门针对土石混合体进行的室内大三轴试验较少,可供参考的完整资料则更少。实际上,近年来试验研究较多的堆石料和粗粒土就是一种特殊的土石混合体。文献[20]中较详细地介绍了一种堆石料的室内大三轴试验,并采用大球模拟块石针对试验进行了颗粒流数值模拟。文中采用的大三轴试样高为500 mm,直径为200 mm,初始孔隙率为0.253,由砂土和形状极不规则的碎石组成,基本无黏结,试样级配见表1,分别进行了围压为0.2,0.4,0.6 MPa的排水剪切试验及相应的颗粒流数值模拟。

表1 土石混合体重塑样颗粒级配
4.2基于不规则颗粒离散元的土石混合体大三轴数值模拟
文献[20]中采用较大球体来模拟土石混合体中的块石,而为了考虑块石之间的相互嵌入、咬合作用,引入了颗粒间的接触黏结模型,并且将颗粒细观摩擦因数取为1.0,以提高数值试样的峰值强度从而逼近室内试验的结果。虽然采用这种方法能够获得与试验结果基本一致的应力-应变关系,但显然与采用的堆石料基本无黏结的性质不符,同时颗粒间的细观摩擦因数取值也偏大,对于进一步研究土石混合体变形破坏机理显然不合适。因此,有必要建立更加符合实际的土石混合体数值模型,以此开展包括对块石形状、颗粒间的相互作用特征等相关研究。
为此,本文针对文献[20]中的无黏结堆石料大三轴试验,采用不规则颗粒模型来模拟块石,颗粒间无黏结,仅适当考虑细观摩擦作用,建立堆石料(土石混合体)大三轴数值模型,开展颗粒流数值试验,并与试验结果进行比较。
4.2.1数值试样的生成
本研究所建立的大三轴数值试样与文献[20]中室内试验所采用的试样大小一致。根据Medley[21]的研究,土石混合体中土/石阈值可定义为
(5)
式中:dS/RT为土/石阈值;LC为土石混合体的工程特征尺度,对于三轴试验试样,可取为试样直径。
本文所研究的大三轴试样直径为200 mm,因此相应的土/石阈值为10 mm,即将粒径≥10 mm的颗粒作为块石处理,而粒径<10 mm的颗粒作为土体处理。根据室内试验试样级配情况(见表1),并考虑到计算效率,土颗粒占38.41%,采用基本球体模拟,粒径在1~10 mm范围内正态分布;块石颗粒占61.59%,采用不规则块石模型模拟,其粒径分为2个粒组,分别在10~20 mm(占28.77%)和20~40 mm(占32.82%)范围内服从正态分布。采用第3节所述的不规则块石随机几何模型及其数值模型建模方法,建立10~20 mm和20~40 mm两个粒组范围内不规则块石的离散元数值模型库。建模时,不规则块石粒径、球度、凹凸度等均在给定范围内服从相应的概率分布。为满足统计规律,所建立的不规则块石数值模型库应包括不少于100个粒径的随机颗粒。
建立不规则块石随机颗粒数值模型库以后,即可建立土石混合体大三轴数值试样,步骤如下:
(1) 将不规则块石随机投放到试样范围内的任意位置,并且保证投放的块石颗粒不重叠。本文提出一种简单实用的方法,即利用PFC3D中generate命令生成的球体不会重叠的特点,在比试样较高一些的空间中生成较大数目的、粒径较大的球体(目的是使投放的块石不重叠),则这些球体的球心坐标是随机的,将这些坐标输出即可获得足够的空间随机点坐标。任意选取一个随机点的坐标,随机选择数值模型库中的不规则块石颗粒球坐标文件,利用C++语言编制程序将选择的块石颗粒平移到选取的随机点上,同时进行随机旋转,这样就投放了一个不规则块石颗粒;重复上述步骤,选取其他随机点的坐标,继续投放块石颗粒,直到块石颗粒的总体积达到试样级配要求。所有块石投放完成以后,需要在PFC3D数值平台上运行块石颗粒文件,查看有无接触(防止发生重叠),若无接触即满足要求;若存在接触,则需要继续加大空间高度或球体直径,重新投放。
(2) 不规则块石随机投放完成并通过无重叠检查后,即可采用PFC3D中内嵌fish语言编制程序在加高的试样空间范围内生成满足级配要求的土颗粒(基本球体),然后使生成的块石颗粒和土体颗粒在自重作用下自由下落,并达到平衡。
(3) 在颗粒上方生成墙,将试样高度压缩至500 mm,并循环至平衡,即可得到一个密实度、块石分布与实际情况类似的土石混合体大三轴数值试样,如图9(a)所示。为了对比,本文还建立了以较大球体模拟块石、其它条件相同的数值试样,如图9(b)所示。图9中,土颗粒为蓝色的球体,块石为绿色的clump或较大球体。

图9 土石混合体大三轴数值试样Fig.9 Numerical specimens of SRM forlarge scale triaxial test
4.2.2细观参数和试验方法
参考土石混合体数值模拟的相关文献[1,3,9-10]和室内试验应力-应变曲线[20],经过反复试算,得到1组颗粒细观参数(见表2)。由于文献[20]试验所用堆石料基本无黏结,因此,本文的数值试验中也不考虑颗粒之间的黏结。压力室侧向约束应为柔性,数值试验中一般取圆筒的法向刚度为颗粒法向刚度的1/10~1/2;上下加载板应为刚性,其法向刚度应大于颗粒法向刚度。本文所取上下加载板的法向刚度为2×108N/m,侧向圆筒的法向刚度为2×105N/m,加载板和侧向圆筒的切向刚度和摩擦因数均为0,即将压力室理想为无摩擦的刚性墙。

表2 土石混合体细观力学参数
进行数值试验时,首先利用伺服控制程序施加围压并保持围压恒定,然后逐步施加轴压。轴压以应变控制方式施加,以模型的上下边界墙作为加载板,加载速度为0.1 m/s。需要说明的是数值试验中的加载速度不同于真实的室内试验中的加载速度[22]。
4.2.3结果分析
限于篇幅,本文仅给出围压为0.2 MPa和0.4 MPa下室内试验和数值试验的偏应力-轴向应变关系曲线和体变-轴向应变关系曲线对比图,如图10和图11所示。

图10 偏应力-轴向应变关系曲线Fig.10 Curves of axial deviatoric stress vs. axial strain

图11 体变-轴向应变关系曲线Fig.11 Curves of volumetric strain vs. axial strain
由图10可见,土石混合体室内大三轴试验所得偏应力-轴向应变关系曲线大致可以分为3个阶段,即压密阶段、应力强化阶段和塑性流动阶段。当轴向应变较小(<1%)时,试样主要表现为压密,偏应力-轴向应变关系曲线近似为直线段;试样屈服后,进入应力强化阶段,由于试样中块石的存在,偏应力-轴向应变关系曲线呈现一种台阶式上升的特征;偏应力达到峰值后,试样随即进入塑性流动状态。与均质土体的变形特征不同的是应力强化阶段,当土颗粒变形较大时,块石颗粒逐步开始接触、咬合,并随着应力的进一步增大可能产生滑移、错位,在偏应力-轴向应变关系曲线上就呈现出台阶式上升特征。
由图10可知,本文进行的2种数值模拟试验都能够描述堆石料(土石混合体)的偏应力-轴向应变曲线的基本特征。很明显看出,块石为随机不规则体的数值试样的应力-应变曲线与室内试验曲线吻合较好,而块石为较大球体的数值试样的曲线峰值强度与室内试验结果相差甚远,围压越大,这种差别也越大。
由图11可知,土石混合体在较低围压(0.2 MPa)下,先表现出一定的剪缩性,在峰值应力附近进入剪胀阶段。而在较高围压(0.4 MPa)下室内试验的试样剪缩程度增大,剪胀不明显。由图11中的数值模拟结果可见,块石为随机不规则体的数值试样能够模拟试样的剪缩性和剪胀性,在初始阶段表现出的剪缩趋势与室内试验基本一致,但随后的剪胀趋势与试验结果存在一定的偏差,主要原因可能是数值试验中侧墙只能发生整体位移,而不能像室内试验中试样周围的橡皮膜和压力室的水那样调整试样边缘局部的不规则变形。块石为较大球体的数值试样很难模拟土石混合体的剪胀性,其剪缩程度较室内试验也偏大,主要原因是球形颗粒易于错动、旋转,颗粒位置能快速调整。
5结论
为了更加真实地模拟土石混合体的物理力学特征,本文提出了一种基于不规则块石球度和凹凸度的随机几何模型生成技术,并建立了相应的数值模型,然后采用无底圆筒堆积试验进行了数值验证,最后建立了符合宏观统计规律的土石混合体三维离散元随机模型,开展了土石混合体室内大三轴试验的颗粒流数值仿真。本文的主要结论如下:
(1) 本文提出的以球度和凹凸度作为几何模型控制参数的建模方法简单实用,只需要经过3步操作即可获得不规则块石的随机几何模型。
(2) 不规则块石颗粒无底圆筒堆积数值试验表明,本文提出的几何模型控制参数不仅能很好地描述块石的不规则形态,而且能很好地体现不规则块石的受力变形特性。
(3) 通过选取合适的颗粒细观参数,建立基于随机不规则块石体的土石混合体数值模型,能很好地模拟土石混合体的应力-应变关系特征,并能够模拟土石混合体的剪缩性和剪胀性。
本文提出的基于不规则颗粒离散元的土石混合体三维离散元模型可以较真实地模拟土石混合体的细观结构特征,为进一步从细观水平上深入研究土石混合体的变形破坏机理奠定了坚实的基础。当然,由于土石混合体中块石形态非常复杂,对于本文随机建模时采用的2个控制参数,尤其是凹凸度,目前还只能通过观察和参数试算对比来确定其取值范围,至于其他简明确定凸凹度取值范围的方法尚需进一步研究。
参考文献:
[1]徐文杰, 胡瑞林, 岳中崎. 土-石混合体随机细观结构生成系统的研发及其细观结构力学数值试验研究[J]. 岩石力学与工程学报, 2009, 28(8): 1652-1665.
[2]油新华. 土石混合体的随机结构模型及其应用研究[D]. 北京: 北方交通大学, 2001.
[3]GRAZIANI A, ROSSINI C, ROTONDA T. Characterization and DEM Modeling of Shear Zones at a Large Dam Foundation[J]. International Journal of Geomechanics, 2012, 12(6): 648-664.
[4]李晓, 廖秋林, 赫建明. 土石混合体力学特性的原位试验研究[J]. 岩石力学与工程学报, 2007, 26(12): 2377-2384.
[5]COLI N, BERRY P, BOLDINI D. In Situ Non-conventional Shear Tests for the Mechanical Characterization of a Bimrock[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 95-102.
[6]董云. 土石混合料强度特性的试验研究[J]. 岩土力学,2007, 28(6): 1269-1274.
[7]刘建锋, 徐进, 高春玉, 等. 土石混合料干密度和粒度的强度效应研究[J]. 岩石力学与工程学报, 2007, 26(增1): 3304-3310.
[8]XU Wen-jie, YUE Zhong-qi, HU Rui-lin. Study on the Mesostructure and Mesomechanical Characteristics of the Soil-rock Mixture Using Digital Image Processing Based Finite Element Method[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(5): 749-762.
[9]贾学明, 柴贺军, 郑颖人. 土石混合料大型直剪试验的颗粒离散元细观力学模拟研究[J]. 岩土力学, 2010, 31(9): 2695-2703.
[10]丁秀丽, 李耀旭, 王新. 基于数字图像的土石混合体力学性质的颗粒流模拟[J]. 岩石力学与工程学报, 2010, 29(3): 477-484.
[11]杜欣, 曾亚武, 高睿,等. 基于CT扫描的不规则外形颗粒三维离散元建模[J]. 上海交通大学学报, 2011, 45(5): 711-715.
[12]CHO G C, DODDS J, SANTAMARINA J C. Particle Shape Effects on Packing Density, Stiffness, and Strength: Natural and Crushed Sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(5): 591-602.
[13]BANGARU R S, ANIMESH D. Aggregate Shape Characterization in Frequency Domain[J]. Construction and Building Materials, 2012, 34: 554-560.
[14]孔亮, 彭仁. 颗粒形状对类砂土力学性质影响的颗粒流模拟[J]. 岩石力学与工程学报, 2011, 30(10): 2112-2119.
[15]MATSUSHIMA T, CHANG C S. Quantitative Evaluation of the Effect of Irregularly Shaped Particles in Sheared Granular Assemblies[J]. Granular Matter, 2011, 13(3): 269-276.
[16]宋来忠, 彭刚, 姜袁. 混凝土三维随机参数化骨料模型[J]. 水利学报, 2012, 43(1): 91-98.
[17]NASSAUER B, LIEDKE T, KUNA M. Polyhedral Particles for the Discrete Element Method[J]. Granular Matter, 2013, 15(1):85-93.
[18]徐文杰, 胡瑞林, 岳中崎. 土石混合体细观结构及力学特性数值模拟研究[J]. 岩石力学与工程学报, 2007, 26(2): 300-310.
[19]Itasca Consulting Group, Inc. Universal Distinct Element Code Version 3.1[M]. Minneapolis: Itasca Consulting Group, 2006.
[20]邵磊, 迟世春, 贾宇峰. 堆石料大三轴试验的细观模拟[J]. 岩土力学, 2009, 30(增): 239-243.
[21]MEDLEY E W.The Engineering Characterization of Melanges and Similar Block-in-matrix Rocks (Bimrocks)[D]. Berkeley, CA: Department of Civil Engineering, University of California, 1994.
[22]CHO N, MARTIN C D, SEGO D C. A Clumped Particle Model for Rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(7): 997-1010.
(编辑:黄玲)
Three-dimensional Stochastic Model of Soil-rock Mixture and ItsNumerical Experiments Based on DEM of Irregularly Shaped Particles
JIN Lei, ZENG Ya-wu, YE Yang, XIA Lei
(School of Civil Engineering, Wuhan University, Wuhan430072, China)
Abstract:In order to simulate the physic-mechanical properties of soil-rock mixture (SRM) realistically, a technique based on sphericity and angularity to constructing random geometric and discrete element method (DEM) model of irregularly shaped (IRS) rock block is proposed. Then particle flow simulations for open bottom cylinder tests of IRS rock blocks under different sphericity and angularity parameters are conducted. Finally, three dimensional (3-D) stochastic models of SRM which conform to the macroscopic statistical rule are established and DEM numerical simulations of large scale triaxial test are conducted. The numerical results and laboratory results are compared and analyzed. It is noteworthy that the proposed modeling method is simple and practical. The modeling controlling parameters are reasonable and effective. It is also indicated that particle flow simulation of SRM with stochastic IRS rock blocks can reproduce the physical and mechanical properties of SRM well, including mesoscopic contacting characteristics of IRS particles, stress-strain relationship, negative dilatancy and positive dilatancy. The proposed method in this paper provides an effective way to further study the deformation and failure mechanism of SRM.
Key words:soil-rock mixture (SRM); irregularly shaped (IRS) particles; 3D-DEM; open bottom cylinder test; large scale triaxial test
中图分类号:TU 44
文献标志码:A
文章编号:1001-5485(2016)05-0094-08
doi:10.11988/ckyyb.201501862016,33(05):94-101
作者简介:金磊(1989-),男,安徽安庆人,博士研究生,主要从事岩土体变形破坏机理等方面的研究,(电话)18062654787(电子信箱)whujinlei@whu.edu.cn。通讯作者:曾亚武(1964-),男,湖北安陆人,教授,博士生导师,主要从事岩石力学与工程方面的教学与研究工作,(电话)13808653023(电子信箱)zengyw@whu.edu.cn。
基金项目:国家自然科学基金项目(41272342)
收稿日期:2015-03-16;修回日期:2015-04-07

