考虑裂纹闭合效应的岩石损伤力学模型及耗散能量分析

温　韬，唐辉明，刘佑荣，王　康，易贤龙，谭钦文

(中国地质大学(武汉) 工程学院,武汉　430074)



考虑裂纹闭合效应的岩石损伤力学模型及耗散能量分析

温韬，唐辉明，刘佑荣，王康，易贤龙，谭钦文

(中国地质大学(武汉) 工程学院,武汉430074)

摘要：针对现有岩石损伤力学模型的局限性，考虑裂纹闭合效应，并引入统计损伤理论，同时提出分布参数确定的方法，建立新型岩石损伤力学模型。该模型更加符合岩石的变形破坏规律，还可以反映岩石的残余强度和延性特征，应用范围更广；与试验结果及前人成果对比，表明模型更为合理可行。不同围压下岩样的损伤变量演化曲线都遵循S型曲线，并可以依据S型曲线对岩石的变形破坏阶段进行划分。裂纹闭合系数(h)对损伤耗能率有较大影响，随着h的减小，损伤耗能率增大，当h达到一定值，岩石破坏阶段对应的损伤耗能率陡增。因此，岩石的变形破坏不仅与其应力状态有关，还与岩石的损伤演化积累以及裂纹闭合效应有关。

关键词：岩石力学；损伤；裂纹闭合系数；损伤耗能率；微元强度

1研究背景

岩石是一种复杂的地质体，岩石的变形破坏伴随着各种缺陷的形成、扩展以及贯通的过程。损伤力学研究材料内部微观缺陷的产生、发展所引起的宏观力学效应以及最终导致材料破坏的过程和规律。Kachanov等[1-2]在研究金属蠕变的过程中，首次引入损伤的概念。在该研究的基础上发展到今天，形成了细观损伤力学、宏观损伤力学和准宏观损伤力学3大块。

对于损伤力学，人们已经开展了广泛而深入的研究，取得了很多研究成果。Krajcinovic等[3-6]基于Weibull分布函数确定岩石的微元强度，建立了岩石损伤统计本构方程。曹文贵等[7-10]在此基础上，从岩石微元强度分布的随机性出发，建立了岩石损伤本构方程，可反映岩石破裂的全过程，尤其是软化特性。温韬等[11]提出影响因子，建立了考虑损伤阈值影响的岩石损伤统计本构模型。杨明辉等[12]探讨了岩石损伤软化统计本构模型参数与岩石软化变形破裂过程的应力-应变全曲线的特征参量的理论关系，建立了本构模型参数新的确定方法。徐卫亚等[13]基于概率论和损伤力学建立了弹塑性损伤统计本构模型，可以反映岩石的剩余强度。杨圣奇等[14]采用损伤力学理论，建立了单轴压缩下能够反映残余强度的岩石损伤统计本构模型。李兆霞[15]通过损伤力学理论探讨了各向同性、各向异性损伤问题及其在工程中的应用。尹光志等[16]从煤岩损伤力学角度出发研究了煤岩内部能量转化机制导出了脆性煤岩损伤能量释放率。笔者[17]分析了砂岩在三轴压缩试验和峰前卸围压试验下的能量变化规律。本文在前人研究的基础上，建立了考虑裂纹闭合影响的岩石损伤本构方程，并找到了模型参数确定的有效方法，所建立的模型能反映不同围压下的应力变化情况；此外，考虑裂纹闭合效应，对损伤耗能率的变化规律进行了详细的分析。

2岩石损伤本构模型的建立

2.1三轴压缩下损伤统计本构方程的推导

统计损伤理论建立岩石变形的全过程模拟主要有2个方法：其一，基于J.Lemaitre应变等价理论建立岩石损伤模型；其二，基于破损理论和岩土材料力学性质的改变程度建立岩土损伤模型。

基于J.Lemaitre应变等价理论，可以建立如下岩石损伤本构关系：

(1)

式中： [σ*]为有效应力矩阵；[σ]为名义应力矩阵；[c]为岩石弹性矩阵；[ε]为应变矩阵；D为岩石损伤变量；h为裂纹闭合系数，0≤h≤1。

若破坏前岩石微元的应力-应变关系符合虎克定律，则可得岩石弹性损伤本构方程为

(2)

假设岩石的破坏准则通式为

(3)

式中:k0为与材料黏聚力和内摩擦角有关的常数； σ*为有效应力。F=f(σ*)反映了岩石微元破坏的危险程度，可以用它作为岩石微元的强度。

由于岩石内部缺陷分布的随机性，岩石的强度也必然是随机的。假设岩石强度服从Weibull分布，其概率密度函数为

(4)

式中:F为微元破坏Weibull分布的强度变量；m与F0均为Weibull分布参数。以岩石微元破坏概率作为损伤变量D，由此可得岩石的损伤变量即统计损伤演化方程为

(5)

可以看出，只要确定了岩石微元强度就确定了损伤变量D。

目前岩石力学中已认可的破坏准则的表现形式有很多，由于德鲁克-普拉格破坏准则具有参数形式简单、适用于岩土介质等优点，本文选用德鲁克-普拉格破坏准则确定岩石的微元强度F,其表达式为

(6)

考虑假三轴条件可得：

(7)

(8)

(9)

(10)

将式(10)代入式(7)、式(8)可得I1和J2：

(11)

(12)

由式(2)、式(5)可得三轴压缩情况下的损伤统计本构模型为

(13)

2.2分布参数的确定方法

根据上述2个条件，由式(13)可以求出参数m与F0：

(14)

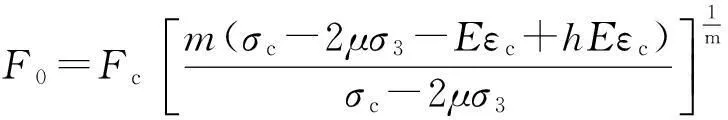
(15)

将式(6)、式(14)和式(15)代入式(13)得到本文的岩石损伤本构模型，其中裂纹闭合系数h可以通过假设岩样受载前后体积不可压缩求得，但它存在不少缺陷，本文采用新方法进行计算。

当岩石破坏处于残余强度时，假设此时的损伤变量D=1，故本文引入的裂纹闭合系数h可以通过式(13) 求得。设残余强度对应的应力、应变分别为σr,εr，则可得出裂纹闭合系数h为

(16)

2.3模型的改进

该模型仅仅适用于特定围压下应力-应变的情况，若能将其用于不同围压下，则该模型更具普遍意义。从文献[9]可知σc和εc的值与围压有关，因此可以根据试验数据建立它们与围压的关系式。

由Mohr-Coulomb准则可得

又因为εc和σ3呈线性关系，即

(18)

式中a和b为常数，结合试验数据并根据式(17)、式(18)可得到σc和εc与围压的关系式。然后代入式(14)、式(15)，最后代入式(13)得到本文改进的岩石损伤力学本构模型。

此外，在计算弹性模量和泊松比时，考虑到围压σ3对岩石的变形破坏有影响，文中的弹性模量E和泊松比μ按式(19)计算。

(19)

式中：σ1，σ3分别为轴向应力和环向应力；ε1，ε3分别为轴向应变和环向应变;B为环向应变与轴向应变的比值。

3实例与验证

为了验证本文改进的损伤本构方程的合理性，选取岩样进行试验研究。岩样来自锦屏某高边坡区厚70 m、青灰色的厚层—块状变质石英细砂岩(T2-3z3(1-1))。对岩样进行三轴压缩试验，通过相应的数据处理可得其岩石内摩擦角φ=39.3°，凝聚力c=25.9 MPa，单轴抗压强度σc=109.1 MPa，其他力学参数见表1。

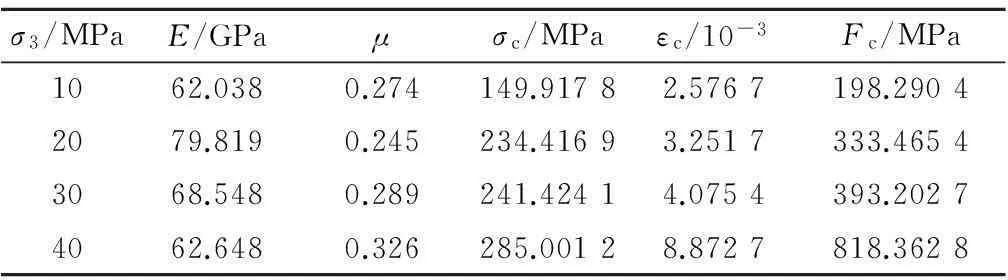
表1　岩样力学参数

经选择不同的h值代入本文提出的岩石损伤力学模型，得出不同裂纹闭合系数下的本构方程，对h选取了1,0.98,0.96,0.94,0.92,0.9,0.8七个值进行分析，当h=1时所得本构方程即为文献[10]所提出的岩石损伤本构方程。不同围压、不同h值时Weibull分布参数m,F0见表2。

从表2可知，m和F0的大小不仅与围压有关，还与h值有关。其中围压越大，m值越小，F0值越大；裂纹闭合系数h越小，m值越大，F0值越小；并且低围压(10，20，30 MPa)时，随着h的的减小，m和F0的变化值也较小，当h值变化0.02时，围压10，20，30 MPa情况下，F0的变化值分别约为0.6,1.6,3.2；高围压(40 MPa)下，m和F0的变化值较大， 当h值变化0.02时，F0的变化值达25以上。说明高围压下，裂纹闭合系数h对m,F0的影响更加显著。

表2　不同围压、不同h值时Weibull分布参数m和F0

图1　试验曲线与理论曲线的比较Fig.1　Comparison of curves between theoreticaland measured values

图1为理论曲线与试验曲线的比较。从图1可知，峰值前，h值对应力-应变曲线影响不大；峰值后，h值对应力-应变曲线影响更加显著。随着h的减小，岩石的残余强度有所增大，并且峰后延性特征更加明显，说明裂纹闭合系数h可以反映岩石的残余强度特征。当h=0.9和0.92时，所得理论曲线与试验曲线吻合程度较好，因此，选择不同的h值，本文的损伤力学模型就可以模拟反映岩石残余强度以及延性特征在内的损伤力学本构方程。

通过将本文理论曲线与试验曲线和文献[10]曲线(即h=1理论曲线)进行比较，可以看出本文模型存在以下特点：

(1) 分布参数的确定方法更具有目的性，本文求解的分布参数更符合实际。

(2) 本文引用了裂纹闭合系数h，将其代入本构方程，能够反映裂纹对应力-应变曲线的影响，更加符合岩石的变形破坏规律，还可以反映岩石的残余强度和延性特征，使之更符合工程实际，具有较高的实用价值。

(3) 与文献[10]理论曲线相比，本文理论曲线与试验曲线能够较好地匹配，充分反映岩体的应变软化特性，并能够很好地反映岩石变形破坏全过程。

图2为根据式(5)得出的不同围压下岩样的累积损伤变化曲线，表明不同围压下岩样的损伤演化曲线单调递增，当达到屈服强度时，损伤变量的增长速率加快。初始加载时岩样的应变量小，其损伤变量也较小，劣化不明显或无劣化。随着加载的进行，应变量增大，岩样内部微裂纹相互摩擦、扩展，损伤累积增大，它是一个汇聚损伤累积的过程。很明显，不同围压下岩样的损伤变量演化曲线都遵循S型曲线，该曲线的特征是初始阶段，曲线近乎水平；中间阶段，曲线迅速上升；终了阶段，曲线斜率逐步减小。该类型曲线能够很好地反映岩石压缩过程中的不同变形阶段：

(1) 弹性变形至微破裂稳定发展阶段，对应图中损伤变量的缓慢增长阶段，几何上为向上凹，微观上表现为可恢复的弹性变形，伴随局部少量微裂纹的出现。

(2) 非稳定破裂发展阶段(或累进性破裂发展阶段)，对应图中的损伤累积速率迅速增加阶段，该阶段微裂纹的发展发生了质的变化，轴向应变和体积应变速率迅速增大，裂纹不断发展。

(3) 破坏后阶段，对应图中的损伤累积速率减小阶段，几何上为向上凸，其内部结构完全破坏，裂纹也已贯通。因此，可以构建适用于该变形破坏过程的损伤演化过程曲线。

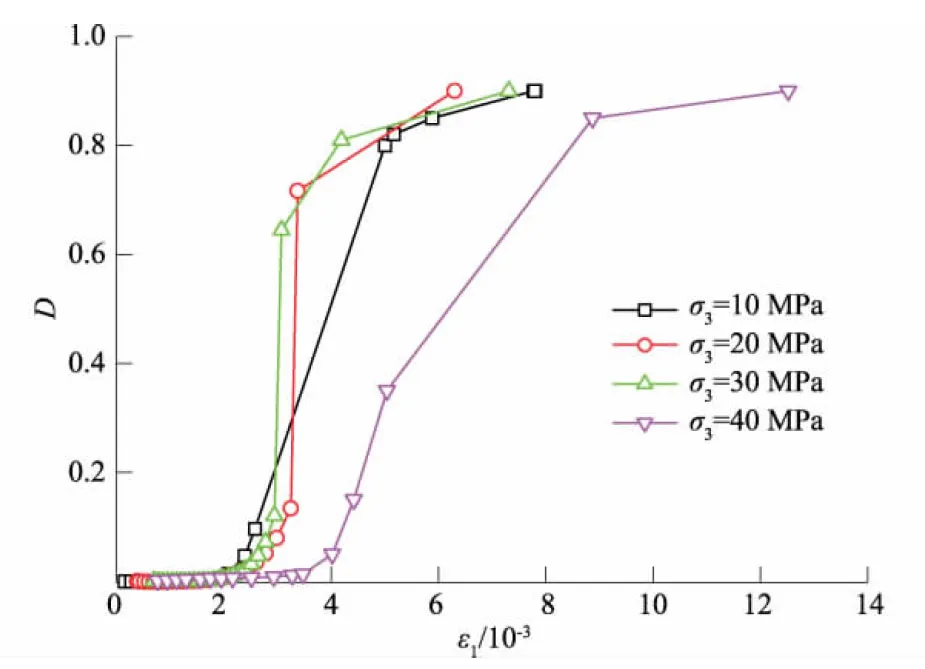
图2　不同围压下岩样的损伤变量曲线Fig.2　Curves of damage variable of rock specimenunder different confining pressures

4耗散能量分析

本文中的损伤耗能率是基于自由能的塑性部分和弹性损伤部分无关的假设，从可观察变量的自由能位势导出的，损伤耗能率还可被定义为恒应力和恒温条件下与损伤变化对应的弹性应变能变化量的一半[19]。

假设塑性应变与弹性应变之间不存在耦合，即弹性模量对塑性应变的影响很小，可忽略不计；微塑性与弹性之间仅有部分耦合；损伤与塑性之间也没有直接的耦合[15]。所以本文微塑性忽略不计，仅考虑裂纹闭合系数h的影响。

在一维问题中，有效应力可以修正为

(20)

本文仅考虑压缩情况，根据热力学第一、第二定律，用损伤变量D定义损伤耗能率[15]为

(21)

则有

(22)

又因为

可以啊。坐在后排的辛娜仰躺着摆出一个奇怪的姿势，左腿像一条倒空了的麻袋，更像残荷枯败的颓枝。你看，我不是幸好少了一条腿吗？

(23)

(24)

将式(23)、式(24)代入式(22)，得

(25)

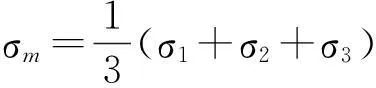
(26)

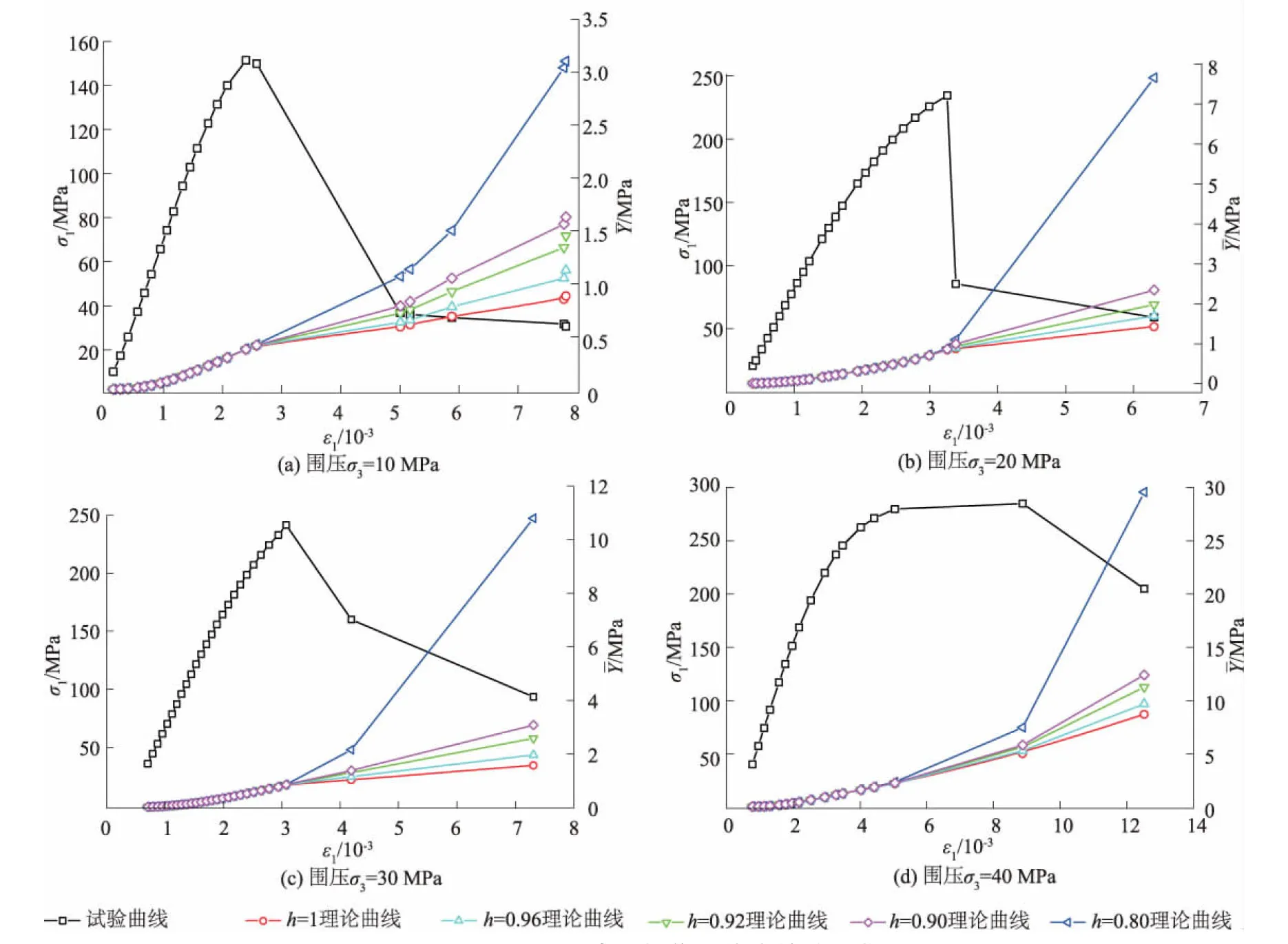
图3　不同围压下岩石损伤耗能率的关系曲线Fig.3　Curves of damage energy dissipation rate of rock under different confining pressures

再将式(5)代入式(26)得出损伤耗能率的计算式。此时裂纹闭合系数h的取值是分析损伤耗率的关键。

图3为不同围压下岩石损伤耗能率的关系曲线。由图3可知，从加载开始，损伤耗能率较小；峰值强度之后，损伤耗能率增长速率加快，且随着围压的增大，岩石达到残余强度时对应的损伤耗能率越大。裂纹闭合系数h对损伤耗能率有较大影响，随着h的减小，对应的损伤耗能率增大，当h达到0.8时，岩石破坏阶段对应的损伤耗能率陡增。说明峰值前岩石变形以弹性为主，塑性变形量较小，故前期损伤耗能率较低；峰值后，岩石内部的微裂纹迅速扩展、贯通，形成宏观裂纹，微裂纹的扩展体现了突变性，故损伤耗能率快速增加。裂纹闭合系数越小，接近峰值点或超过峰值点以后，岩石内部损伤加剧越快，宏观表现为应变软化阶段，储存的弹性应变能逐渐转化为因损伤而消耗的能量，故损伤耗能率越大。因此，岩石的变形破坏不仅与其应力状态有关，还与岩石的损伤演化积累以及裂纹闭合效应有关。

图4和表3为不同σ3和h下，裂纹闭合效应所对应的岩样破坏后的损伤耗能率。

图4　不同h值对应破坏后的损伤耗能率曲线Fig.4　Curves of damage energy dissipation ratein the presence of different h values

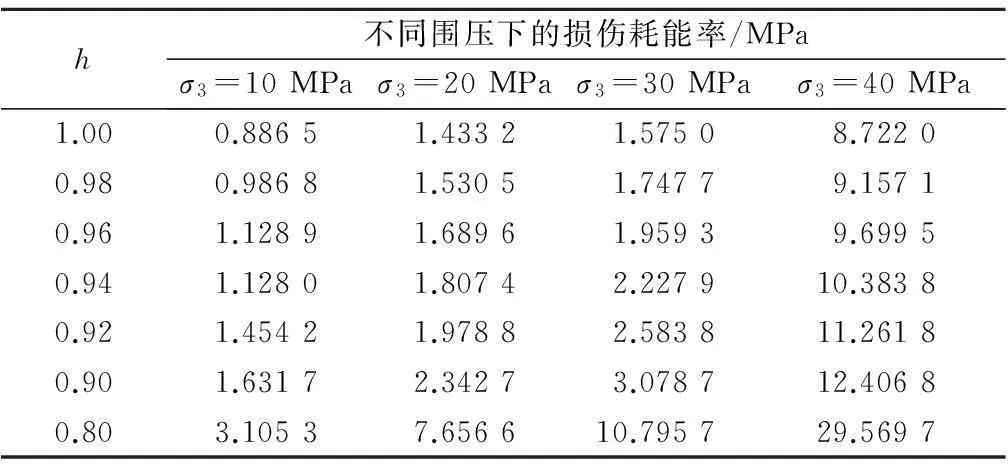
h不同围压下的损伤耗能率/MPaσ3=10MPaσ3=20MPaσ3=30MPaσ3=40MPa1.000.88651.43321.57508.72200.980.98681.53051.74779.15710.961.12891.68961.95939.69950.941.12801.80742.227910.38380.921.45421.97882.583811.26180.901.63172.34273.078712.40680.803.10537.656610.795729.5697

5结论

本文结合岩石应变强度理论以及岩石微元强度服从Weibull分布的假设，引入裂纹闭合系数，从而提出更加完善的岩石损伤力学模型，该模型具有更广的适用性，能更好地表征岩石的本构关系。并且通过引入损伤耗能率，研究了考虑裂纹闭合效应的耗散能量的变化规律，得出如下主要结论：

(1) 低围压下，裂纹闭合系数对m，F0的影响较小；高围压下，该影响更加显著。

(2) 针对现有岩石损伤力学模型的局限性，本文提出裂纹闭合系数建立新的损伤本构方程，使其应用范围更广，更加符合岩石的变形破坏规律，还可以反映岩石的残余强度和延性特征；与试验结果和前人成果比较分析，表明本文模型更为合理可行。

(3) 裂纹闭合系数h对损伤耗能率具有较大影响，随着h的减小，损伤耗能率增大，当h达到一定值，岩石破坏阶段对应的损伤耗能率陡增。

参考文献：

[1]KACHNOV M. Effective Elastic Properties of Cracked Solids: Critical Review of Some Basic Concepts [J]. Applied Mechanics Reviews, 1992, 45(8):304-335.

[2]KACHANOV M, TSUKROV I, SHAFIRO B. Effective Modulus of Solids with Cavities of Various Shapes[J]. Applied Mechanics Review, 1994, 47(Sup.1): 151-174.

[3]KRAJCINOVIC D. The Continuous Damage Theory of Brittle Materials[J]. Journal of Applied Mechanics, 1981，48(8) : 809-822.

[4]KRAJCINOVIC D. Statistical Aspects of the Continuous Damage Theory[J]. International Journal of Solids and Structures, 1982, 18(7): 551-562.

[5]KRAJCINOVIC D，SILVA M A G. Statistical Aspects of the Continuous Damage Theory[J]. International Journal of Solids and Structures, 1982, 18(7): 551-562.

[6]谢和平．岩石、混凝土损伤力学[M]．江苏徐州：中国矿业大学出版社，1990.

[7]曹文贵，赵明华，刘成学．基于统计损伤理论的德鲁克-普拉格岩石强度准则的修正[J]．水利学报，2004，(9)：18-23.

[8]曹文贵，莫瑞，李翔．基于正态分布的岩石软硬化损伤统计本构模型及其参数确定方法探讨[J]．岩土工程学报， 2007，29(5)：671-675.

[9]曹文贵，李翔，刘峰．裂隙化岩体应变软化损伤本构模型探讨[J]．岩石力学与工程学报，2007，26(12)：2488-2494.

[10]曹文贵．岩石损伤软化统计本构模型之研究[J]． 岩石力学与工程学报， 1998，17(6)：628-633.

[11]温韬，唐辉明，刘佑荣，等.影响因子修正的新型岩石损伤统计本构模型[J].中国矿业大学学报(自然科学版)，2016，45(1)：142-150.

[12]杨明辉，赵明华，曹文贵．岩石损伤软化统计本构模型参数的确定方法[J]．水利学报，2005，36(3)：345-349.

[13]徐卫亚，韦立德．岩石损伤统计本构模型的研究[J]．岩石力学与工程学报，2002，21(6)：787-791.

[14]杨圣奇，徐卫亚，韦立德，等．单轴压缩下岩石损伤统计本构模型与试验研究[J]．河海大学学报(自然科学版)，2004，32(2)：200-203.

[15]李兆霞．损伤力学及其应用[M]．北京：科学出版社，2002：16-19.

[16]尹光志， 张东明．脆性煤岩损伤模型及冲击地压损伤能量指数[J]．重庆大学学报：自然科学版， 2002，25(9)：75-78.

[17]温韬，刘佑荣，胡政. 高应力区砂岩加卸载条件下能量变化规律及损伤分析[J]. 地质科技情报，2015，34(2):200-206.

[18]杨光松．损伤力学与复合材料损伤[M]．北京：国防工业出版社，1995.

[19]让·勒墨特黑，余天庆.预估结构中的塑性破坏或蠕变疲劳破坏的损伤模型[J].固体力学学报，1981，(4):512-525.

(编辑：赵卫兵)

A Rock Damage Mechanics Model and Analysis on Damage EnergyDissipation in Consideration of Crack Closure Effect

WEN Tao, TANG Hui-ming, LIU You-rong, WANG Kang, YI Xian-long, TAN Qin-wen

(Faculty of Engineering, China University of Geosciences, Wuhan430074, China)

Abstract:In view of the insufficiency of the present rock damage mechanics models, we propose a statistical constitutive model of rock damage considering the crack closure effect by introducing the statistical damage theory. The model is more consistent with the deformation and failure regularity of rock, and reflects the residual strength and ductility, hence having a wide range of application. The model is proved to be rational and feasible through comparison with the existing research results and measured data. The curves of damage variable under different confining pressures conform with the “S” shape, which can be divided into different phases according to the deformation failure stages. Crack closure coefficient (h) has great influence on the damage energy dissipation rate. With the decrease of h , damage energy dissipation rate increases; when the value of h reaches a certain value, the damage energy dissipation rate rises sharply. Therefore, the deformation failure of rock is not only related with stress state, but also involves the accumulation of damage evolution and crack closure effect.

Key words:rock mechanics; damage; crack closure effect; damage energy dissipation rate；micro element strength

中图分类号：TU45

文献标志码：A

文章编号：1001-5485(2016)05-0069-07

doi:10.11988/ckyyb.201501382016,33(05):69-75

作者简介：温韬(1990-)，男，江西宜春人，博士研究生，从事工程地质与岩土工程方面的研究，(电话)13476117745(电子信箱) wentao200840@sina.com。

收稿日期：2015-02-16；修回日期：2015-03-27