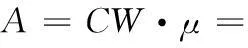基于优化集对分析模型的水质综合评价方法
黄 瑞,张防修
(1.河海大学 环境科学学院,南京 210000;2.扬州市职业大学 资源与环境工程学院,江苏 扬州 225000)
基于优化集对分析模型的水质综合评价方法
黄瑞1,2,张防修1
(1.河海大学 环境科学学院,南京210000;2.扬州市职业大学 资源与环境工程学院,江苏 扬州225000)
摘要:针对标准集对分析存在同异反评语细化问题,对传统模型进行改进。在水质权重确定过程中,因单一采用主观确权法或客观确权法均存在缺陷,提出综合确定权值的思路。选用改进后的AHP法主观确权和熵权系数法客观确权,然后依据最小鉴别信息原理进行综合确权,提高了权重确定的科学性。将新方法运用在大伙房水库水质评价中,将评价结果与基于模糊评价法、BP神经网络法的评价结果进行比较。结果表明新方法能更贴近实际,反映水质特征,具有良好的应用前景。
关键词:水质评价;集对分析;组合权重;AHP法;大伙房水库
1研究背景
水质评价是指依据水质对居民生活、生产的适宜程度,根据预先设定的评价目标,选择相关水质参数、评价标准和水质评价方法,开展水体的利用价值评价。常用方法主要为确定性方法与不确定性方法2类。确定性方法包括单因子指数法及综合指数法,由于计算简单、便于操作,在国内水质评价实践中被大量采用[1-3]。不确定性方法包括数理统计分析、灰色理论、模糊集理论、人工神经网络等,在应用中各有特点,但也存在不足之处,如数理统计分析需以大量实测数据为前提;灰色理论概念清楚,操作性强,但评价值趋向平均、分辨效果不佳[4];模糊评价中的取大取小处理思路,运算简单便捷,但在处理过程中容易发生信息丢失,尤其当评价指标分散,各指标的权重均较小时,可能会得不出结论[5];运用人工神经网络方法,处理过程存在收敛速度慢、易陷入局部极小点,无法得到全局最优点等缺点[6]。
水环境质量测评需要对系统中的多维变量进行细致分析,这对评价模型提出了很高的质量要求。集对分析是在一定的问题背景下,对2个集合的确定性与不确定性进行系统分析的一种数学方法,它通过层次性的分析水质评价值的确定性程度,逐步给出细致严谨的评价结果。该方法可以研究水环境系统中广泛存在的不确定因素及相互之间复杂的变化关系。集对分析方法已在灾害预测和水资源预测等领域获得应用。针对传统集对分析方法存在同异反评语细化问题[7]以及评价指标权重值设定不合理的问题[8]。本研究对传统方法进行优化,细化评价分类。在水质指标权重值的确定过程中,提出组合主客观评价方法,优化权重评价值。改进后的评价方法能更准确地反映被评价水环境特征。
2优化集对分析评价模型
2.1标准集对分析评价模型

(1)

2.2优化标准集对分析模型
标准集对分析方法将2个集合的所有特性粗略地划分为3类,这种分类方法能满足一些简单对象的分类要求,但针对一些具有高维信息特征的对象,这种评价方法显得过于简单。根据联系度可展性原理,应对差异度b、对立度c作深入的细化分类。
在水质评价中,对于水质样本集合C、水质标准集合U有
式中:Cij为第i个样本第j项评价值,i=1,2,…,m,j=1,2,…,n;Uij为第j项指标第k级别限值,k=1,2,…,p。
开展水质样本C和水质标准U 2个集合的比较分析,对于越小越优型指标,若U(i-1)j≤Cij≤Uij,则认为是相同,a=1,且b1,b2,c1,c2均为0。若Cij
(2)
其中:a+b1+b2+c1+c2=1;i+∈[0,1],i-∈[-1,0],且i++i-=i∈[-1,1];j+={0,1},j-=-1。
待评价水质样本对应5类水质级别的同异反联系度按式(3)至式(7)准则确定。
(3)
(4)

(5)
(6)
(7)
模型中U1j,U2j,U3j,U4j,U5j分别为《地表水环境标准》(GB 3838—2002)中5类水质界限值。
3水质评价指标权重的确定
3.1传统水质指标权重确定方法
水质指标的权重确定是水质评价研究的难点之一。常用方法分主观赋权法和客观赋权法2类[9-10]。主观赋权法无需样本数据,主要依靠决策者的主观信息进行决策,如层次分析法、专家调查法等。这种方法依赖于决策者的意向,评价结果具有很大的主观性。客观赋权法是根据一定的规则,数据信息自动赋权的一类方法,如主成分法、熵技术法及多目标规划法等。客观赋权结果具有较强的数学理论依据,但是决策过程未能体现决策者的经验和知识信息。国内外学者为了克服采用单一评价方法存在的缺陷,开展了相关专题研究[11-13]。李秋元等[8]运用层次分析法、基于实数编码遗传算法的投影寻踪方法确定主观与客观权重,然后计算组合权重。由于该方法仅仅采用简单的乘法合成归一化方法进行集成,主客观权值的优化组合缺乏必要的理论依据,因此还存在问题。针对现有方法存在的不足,本次研究提出改进解决思路,运用改进AHP(Analytic Hierarchy Process)法确定主观评价值,运用熵权系数法确定客观权重值,然后依据最小鉴别信息原理计算组合权重。该方法兼顾了决策者的主观知识和经验,同时反映了分析对象本身的数据特征。使得评价结果更加符合水质的实际情况。
3.2组合权重值计算
3.2.1主观评价法与客观评价法权重值计算
3.2.1.1基于改进后层次分析法的主观评权计算
传统层次分析法一般建议1—9个评价标度。过高标度设计容易形成错误评价结论,所构建的判断矩阵往往不具有一致性。考虑到在水质评价领域,对水体质量主观分类能力以及各等级水体水质之间的差异性,提出选用6个等级标度开展水质评价。根据标度评价结果的传递性,如果确定了指标A对指标B的相对重要性标度为A∶B,指标B对指标C的相对重要性标度为B∶C,则由传递性可以确定指标A对指标C的相对重要性标度为A∶C。这样就可以建立两两比较的判断矩阵M。求解矩阵M的最大特征值及其特征向量,并将其特征向量归一化,对矩阵M进行一致性检验,即可求得基于改进AHP法的主观权重向量。
3.2.1.2基于熵权系数法计算客观评价权重值
熵权法属于客观赋权方法,处理思路是根据相关水质指标变异程度,利用信息熵计算出熵权,再以熵权为基础,修正各指标的权重,从而优化客观权重值的确定。
对于水质样本集合Cij,首先进行归一化处理,方法如下:
(8)
得到归一化矩阵:
(9)
计算第j个评价指标下第i个评价样本指标特征值比重为
(10)
计算第j个评价指标的熵为
(11)
计算第j个评价指标的权重为
(12)
3.2.2水质权重组合赋权法


(13)
采用拉格朗日乘子法求解上述问题,可得
(14)
4案例分析
将优化集对分析模型应用于大伙房水库水质评价。大伙房水库是国家重点水源地之一,为辽宁省7个市2 300万人提供水源。水库水质好坏直接关系到广大人民群众的生命安全及周边社会经济发展。近年来,有关水质监测结果表明,水质污染和富营养化问题有严重发展趋势。为了更好地保护水库水质,维护周边群众健康,应及时开展水库水质评价。
4.1数据来源
根据大伙房水库的水体特征及开展水质监测的现实条件,本次研究选取7种水质污染因子作为2010年水质评价的分析对象(见表1)。因素集U={u1,u2,u3,u4,u5,u6,u7}={溶解氧,BOD5,高锰酸盐指数,粪大肠菌群,氨氮,总磷,总氮},评价集V={v1,v2,v3,v4,v5}= {Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}。各水质指标值采用《地表水环境质量标准》(GB 3838—2002)(见表2)。
4.2数据评价
以大伙房水库浑73(库末端)监测断面为例,由式(3)至式(7)计算联系度矩阵为
μ=(a+b1i-+b2i++c1j-+c2j+)j×k=

表1 2010年大伙房水库7个断面的水质监测值
注:“ 表2 地表水质量分类指标 基于改进后AHP法,水质评价主观权重值为 SW=[sw1,sw2,sw3,sw4,sw5,sw6,sw7]= [0.059 5,0.059 5,0.143 4,0.139 9,0.205,0.278,0.224 7]。 基于熵权系数法,由式(8)至式(12),水质评价客观权重值为 OW=[ow1,ow2,ow3,ow4,ow5,ow6,ow7]= [0.092,0.092,0.143,0.141,0.171,0.199,0.179]。 基于水质权重组合赋权法,由式(13)和式(14)计算得到组合权重值为 CW=[0.091,0.091,0.141,0.139,0.168,0.195,0.176]。 进行模糊矩阵复合运算,求得浑73(库末端)断面的综合联系度矩阵A为 计算联系度的集对势,scv(u)=a/c,当a/c>1时,则为集对同势,说明评价样本和标准级别在同、异、反联系中存在同一趋势,并且趋值越大同一性越强。若a>c>b,为“强同势”;若a>b>c,为“弱同势”;若b>a>c,为“微同势”,若b=0为“准同势”;当a/c<1时,则为集对反势;当a/c=1时,则为集对均势。 表3为7个监测断面评价结果。由表3可知,水库浑73(库末端)监测断面水质样本对应5类水质标准的集对势分别为:scv(u1)=4.47,scv(u2)=6.51,scv(u3)=4.62,scv(u4)=3.35,scv(u5)=2.36。归一化后,得到浑73(库末端)监测断面对5级的趋同程度分别为:20.97%,30.54%,21.68%,15.72%,11.07%,故水质评价的判断等级为Ⅱ级。 当集对势接近时,会影响评价结果准确判定,这时需要通过比较c1,c2的大小或者区分“强”、“弱”、“微”同势来判定水质级别。 表3 7个监测断面评价结果 为了验证评价模型的合理性,将计算结果与基于综合水质评价、基于模糊评价[15]、基于BP神经网络[16]方法的评价结果进行比较(见表4)。可以看出3种评价方法的评价结果大体一致,仅就北杂木断面水质评价存在异议。此断面的7项水质指标中有2项为Ⅰ级,2项为Ⅱ级,2项为Ⅲ级,1项为Ⅴ级,综合评定为Ⅲ级较为合理。比较集对分析方法和人工神经网络、模糊评价等方法的运算过程,集对分析计算方法思路清晰,运算过程简便,评价分辨率高,且在运算过程中不依赖于主观判断因素,不遗失中间数据信息,因此评价结果更为合理可信,能准确反映水质实际状况。 表4 3种方法评价结果比较 5结论 (1) 针对水环境系统存在高维变量信息特征,对标准集对分析方法提出了改进措施,细化了同、异、反特性,评价模型能更细致地反映水质评价样本与5类水质等级的趋同程度。 (2) 基于改进AHP法的主观权重,基于熵权系数法确定客观权重,并依据最小鉴别信息原理确定各水质指标的主客观综合权重值。这种评价方法合理借鉴了决策者的知识与经验信息,同时又能反映评价数据本身所反映的特征。基于新方法的评价结果更符合水质实际情况。 (3) 将新方法运用于大伙房水库的水质评价,并将评价结果与模糊评价、BP神经网络评价的结果开展比较。结果表明优化集对分析模型评价方法能更准确反映待评价对象的水质特征,是一种可行的评价方法。 参考文献: [1]陈仁杰,钱海雷,袁东,等. 2010.改良综合指数法及其在上海市水源水质评价中的应用[J].环境科学学报, 2010,30(2): 431-437. [2]朱国宇,熊伟. 模糊评价法与综合指数法在生态影响后评价中的应用比较研究[J].东北农业大学学报,2011,42(2):54-58. [3]张鉴, 束龙仓, 张琛, 等. 基于熵权的综合指数法在地下水水质评价中的应用[J]. 水电能源科学,2010,28(8):30-32. [4]富天乙,邹志红,王晓静.基于多元统计和水质标识指数的辽阳太子河水质评价研究[J]. 环境科学学报,2014,34(2) :473-480. [5]黎育红,贺石磊. 基于粗糙-信息熵的水质综合评价方法[J].长江流域资源与环境,2014,23(1):109-116. [6]苏彩红,向 娜,陈广义,等.基于人工蜂群算法与BP神经网络的水质评价模型[J].环境工程学报,2012,6(2):699-704. [7]王颖,邵磊,杨方廷,等.改进的挤兑分析水质综合评价方法[J].水力发电学报,2012,31(3):99-106. [8]李秋元,刘东.组合权重模糊模型在区域地下水水质评价中的应用[J].中国农村水利水电,2014,(3):1-8. [9]胡晓雪,杨晓华,郦建强,等.河流健康系统评价的集对分析模型[J].系统工程理论与实践,2008,(5):164-176. [10]徐兵兵,张妙仙,王肖肖.改进的模糊层次分析法在南苕溪临安段水质评价中的应用[J].环境科学学报,2011,31(9):2066-2072. [11]金菊良,黄慧梅,魏一鸣.基于组合权重的水质评价模型[J].水力发电学报,2004,23(3):13-19. [12]周振民,穆文彬.组合权重可变模糊模型在地表水水质评价中的应用[J].中国农村水利水电,2011,(10):82-86. [13]唐摇影,黄显峰,方国华.基于组合权重的模糊物元评价模型在丰县水质评价中的应用[J].水电能源科学,2014,32(6):37-41. [14]邢军,付芝,孙立波.基于熵权的地下水水质模糊综合评价[J].节水灌溉,2011,(8):5-7. [15]黄瑞,韩龙喜,张鸿,等.基于模糊评价和AHP的大伙房水库水质评价[J].人民黄河,2013,35(4):32-34. [16]马玲玲,周林飞,王铁良.基于BP神经网络的大伙房水库水质综合评价[J].沈阳农业大学学报,2014,45(5):637-640. (编辑:赵卫兵) Method of Comprehensively Evaluating Water QualityBased on Optimal Set Pair Analysis HUANG Rui1,2, ZHANG Fang-xiu1 (1.College of Environmental Science, Hohai University, Nanjing210000, China; 2.College of Resources and Environmental Engineering, Yangzhou Polytechnic College, Yangzhou225000, China) Abstract:This paper proposed an improved set pair analysis model to solve the problem of subtle differentiation between uniform. In view of the defects of using subjective analysis separately, or objective analysis alone, we put forward a new idea of comprehensively determine the weight coefficients. Weight coefficients are calculated by the aid of optimized analytic hierarchy process for subjective weights and entropic coefficients method for objective weights, and then the objective weights and subjective ones are combined according to the minimum discrimination information principle, which improves the veracity of the weight. This method was used to evaluate the water quality of the Dahuofang reservoir, and the result is compared with those from fuzzy set method and BP neural network method. The results show that the new method has good application prospect as it reflects the actual situation and water quality much better. Key words:water quality assessment; set pair analysis; combinational weight;AHP; Dahuofang Reservoir 中图分类号:X824 文献标志码:A 文章编号:1001-5485(2016)05-0006-05 doi:10.11988/ckyyb.201501572016,33(05):6-10,17 作者简介:黄瑞(1980-),男,江苏南通人,副教授,博士,主要从事水环境保护研究, (电话)13773521819(电子信箱)1546028308@qq.com。 基金项目:水利部公益性行业科研专项(201101031) 收稿日期:2014-03-05;修回日期:2015-03-26