基于砂箱模型试验的加筋土挡墙合理布筋方式探讨
张玉广,罗 强,张 良,蒋良潍,谭小英
(西南交通大学 a.高速铁路线路工程教育部重点实验室;b.土木工程学院,成都 610031)
基于砂箱模型试验的加筋土挡墙合理布筋方式探讨
张玉广a, b,罗强a, b,张良a, b,蒋良潍a, b,谭小英a, b
(西南交通大学 a.高速铁路线路工程教育部重点实验室;b.土木工程学院,成都610031)
摘要:针对加筋土挡墙中拉筋水平和垂直间距、筋带宽度和拉筋长度的合理布设问题,根据拉筋所受土压力相等的等土压应力面积法,提出了拉筋水平等间距、垂向沿埋深逐层加密的布置方式及相应的计算式;采用砂箱模型试验,以墙体处于极限稳定状态下的最少用筋面积为条件,探讨了加筋土挡墙的合理布筋方式。试验分析表明:采用与土压力沿深度逐渐增大相适应的拉筋“上疏下密”布置形式可实现筋带均衡受力,在“窄筋密布”的条件下具有更好的稳定性且用筋量更少;与墙后填土潜在破裂楔体呈上宽下窄形状相适应的筋带“上长下短”布置方式稳定性优于“上下等长”布置;采用“窄筋长布”的方式较“宽筋短布”能增加筋带有效锚固面积,提高挡墙稳定性。
关键词:加筋土挡墙;砂箱模型;合理布筋方式;等土压应力面积法;潜在破裂面
1研究背景
现代加筋土技术是由20世纪60年代由法国工程师H.Vidal提出的[1],20世纪70年代引入我国,并得到广泛的应用和发展[2]。众所周知,土体的抗剪强度远大于抗拉强度,在土中加入抗拉性能较好的筋材,形成加筋土,利用土体与筋材界面间的摩擦作用,改善土体的强度和变形特性。随着加筋土技术的不断发展,其应用领域不断扩大,包括挡土墙、边坡、地基等[3]。加筋土挡墙是一种由挡墙面板、拉筋材料和填土三者组成的能适应地基一定变形的柔性轻型支挡结构。由于它具有施工简便,抗震性强,节约占地,造价低等特点,使加筋土挡墙广泛应用于公路、铁路、水利、电力、市政等领域[4]。
对于加筋土挡墙,拉筋的布置方式包括拉筋水平、垂直间距,筋带宽度和拉筋长度,三者对加筋土挡墙结构的稳定性起主要影响作用。然而,过大的拉筋水平、垂直间距或过短的拉筋长度可能导致加筋土挡墙结构产生过量变形,甚至导致其结构整体破坏而失去稳定;反之,则浪费筋材,结构不够经济。所以,如何设计合理的拉筋布置方式是加筋土挡墙支挡结构的关键技术问题之一。
目前,在加筋土拉筋布置方式理论研究方面,杨锡武等[5]基于离心模型试验和断裂理论研究加筋边坡合理布筋方式,认为加筋增加边坡稳定性的效果与布筋方式密切相关,在中下部H/3~H/2高度范围内加密布筋为加筋边坡最合理的布筋方案;雷胜友等[6]利用加筋土三轴试验得出筋材周向布置时的加筋土强度提高效益数比径向布置时大;张孟喜[7]根据有限元分析和试验验证研究加筋土挡墙拉筋的合理布置方向,指出对以自重为主的加筋土挡墙,其最佳布筋方向为下倾角10°左右,且筋条越长,其效果越明显,而超载比例较大时,水平方向布筋效果最好;同时,也有学者从不同角度对加筋间距进行研究,王初生等[8]通过模型试验探讨了沉降与加筋间距和填土荷载的关系,得出加筋垂直间距>50 cm时,模型路堤沉降增量与路堤压力呈正相关,而在加筋垂直间距为30 cm时,该沉降增量随着荷载增加呈减少趋势,逐渐趋于稳定,从而确定柔性桥台合理加筋间距为30~50 cm;包承纲等[9]采用大型叠环式剪力仪进行了土工格栅的拉拔试验,分析格栅与填土之间界面的特性,认为界面两侧一定范围的土体由于应力场的变化而存在间接影响带,此影响范围大致在30 cm左右;O.Bilgin等[10]对比分析了MSE挡土墙的4种不同拉筋材料 (土工格栅、土工布、金属条和金属带) 长度受墙高、附加荷载、拉筋垂直间距和筋材特性等因素的影响规律,认为拉筋长度应在[0.5H,0.7H]范围内。
可见,拉筋的水平、垂直间距,筋带宽度和拉筋长度等几何要素是影响加筋土挡墙稳定的关键因素,其合理布置方式是加筋土挡墙结构设计的首要内容。但现有的加筋土挡墙设计理论并未提出明确的拉筋布置原则,实际工程中多基于经验采用等间距的布置形式。已有研究工作多限于单一因素的规律性分析,鲜有对多因素相互影响下的拉筋合理布置方式的探讨。论文采用等土压应力面积的拉筋布置原则,首先建立水平向等间距、垂向沿墙高逐层加密的拉筋立面布置模式,推导相应计算式;进而基于砂箱模型试验,根据墙体处于极限稳定状态下用筋量最少原则,确定挡墙立面布筋间距及筋带宽度、挡墙剖面拉筋长度等关键参数。研究对完善加筋土挡墙的结构设计有指导意义。
2拉筋合理布置方式分析
对于加筋土挡墙,筋土界面对筋材两侧一定范围内土体的应力状态进行了改变,可视为对土体的间接加固作用。这种间接加固是由于界面受剪时扰动了界面两侧一定范围土体内的颗粒,促使加筋土体强度的增大,确定影响范围的大小,有助于确定筋材布置的合理间距[9]。将筋土界面的影响范围简化为一个长方形,确定每根拉筋影响范围的宽Sx和高Sy,即可确定加筋土挡墙的拉筋水平、垂直布置间距,如图1所示。其中a为单根拉筋宽度。

图1 拉筋影响范围示意图Fig.1 Scope of reinforce-ment effect
加筋土挡墙内部稳定分析大多采用应力分析法和楔体平衡分析法。前者根据拉筋平衡填土中最大拉应力分力的水平应力,假定在挡土墙顶部为静止状态,随深度逐步向主动应力状态变化,深度到6 m以下便为主动应力状态,填料产生的水平土压应力按式(1)计算[11],土压力系数及土压应力分布如图2(a)所示[12];后者通过拉筋承受其影响范围内墙面板所受的土压力,滑动楔体达到平衡状态时,拉筋与填土产生相对位移使墙体处于主动应力状态,土压力系数取主动土压力系数,土压应力分布如图2(b)所示[12]。

(1)
其中,
式中:σ为填料产生的水平土压应力(kPa);γ为加筋体的填料重度(kN/m3);hi为墙顶距第i层拉筋的高度(m);Ki为加筋土挡墙内hi深度处的土压力系数;K0为静止土压力系数;Ka为主动土压力系数,Ka=tan2(45°-φ/2) ;φ为填料综合内摩擦角。

图2 应力分析法和楔体平衡分析法计算示意图Fig.2 Calculation schemes of stress analysis andelastic wedge equilibrium analysis
墙体处于极限稳定状态时,拉筋与填土之间产生相对位移而发挥摩擦作用,填土体已达到主动应力状态,拉筋所平衡的是填土产生的水平主动土压力。因此,墙体的土压力系数取朗肯主动土压力系数。以朗肯土压力理论为基础,对于较简单界面(挡土墙墙背直立、墙后填土面水平、墙背光滑)的无黏性土主动土压力强度与深度z成正比,呈三角形分布[13]。
2.1等土压应力面积法
假设水平土压力全部由筋材承担,每层拉筋承担拉力Ti相等,将水平土压力n等分,如图3所示,等分的土压力由所受拉力相等的拉筋承担,使整个墙体受力均衡,拉筋影响范围内的土压力面积Ai相等,如式(2)所示。
(2)
式中:Ai为第i层拉筋分担的土压应力面积(m2)。
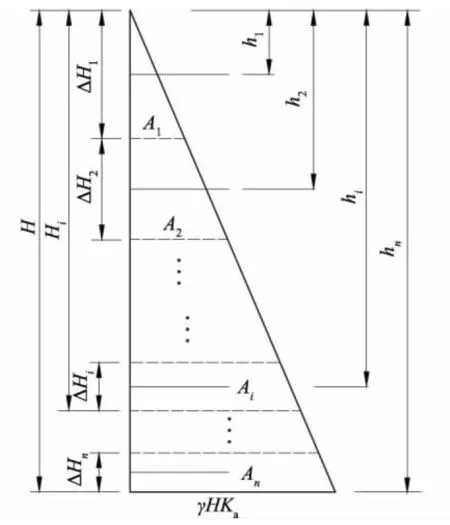
图3 土压力等面积分配示意图
2.2拉筋垂直布置间距

(3)
(4)
(5)
式中:Hi为第i层拉筋所受土压力层底端至挡墙顶端的距离(m)。
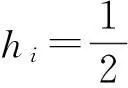
(6)

(7)
(8)
(9)

(10)
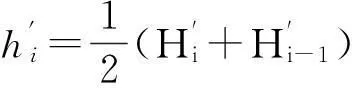
(11)

2.3拉筋水平布置间距
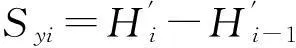
(12)
由于Syi沿填土深度逐渐减小,拉筋的影响面积相应变小,拉筋水平和垂直布置均沿着填土深度逐渐加密,总体呈上疏下密布置形式,如图4(a)。但是,这样的布置形式会使材料和构件的制作及挡墙施工操作变得复杂,为方便施工,将拉筋按水平向等间距布置,其有2种形式:①以挡墙上部较大间距统一布置;②以挡墙下部较小间距统一布置。考虑到结构的经济性和合理性,第2种布置形式间距较小,布置拉筋数较多,用筋量较第1种布置形式大;而挡墙上部最大间距为Sy1,但第1层土压力小,拉筋布置受到边界松弛及填料密实的干扰大,故采用挡墙上部第2层较大间距布置形式,即拉筋水平间距Sx=Sy2如式(13)所示,布置方式如图4(b)所示。

(13)

图4 拉筋立面布置形式
2.4拉筋初始长度
加筋体潜在的破裂面为拉筋最大拉力点的连线,基本上为对数螺旋线,加筋体被拉筋最大拉力点的连线分为活动区和稳定区,可按0.3H简化计算,简化破裂面如图5所示[11]。

图5 “0.3H法”破裂面分界线Fig.5 Fracture surface boundary using “0.3H method”
根据破裂面的分布,将土体分为稳定区和滑动区,拉筋的抗拔性与加筋体的破裂面相关,只有深入破裂面后稳定区的拉筋长度才具有可靠的抗拔力,此段长度为有效锚固长度Lbi;处于滑动区的长度为无效长度Lai[15],有效锚固长度Lbi产生的抗拔力Pfi应大于或等于拉筋所受拉力Ti,如式(14)所示[11],极限稳定状态下取等号,如式(15)所示。
(14)
(15)
式中:σvi为第i层单根拉筋所在位置的垂直压应力,σvi=γhi;a为单根拉筋宽度(m);f为拉筋与填料间摩擦系数。
不考虑附加荷载,进而得有效锚固长度Lbi如式(16)所示,滑动区无效长度Lai如式(17)所示[4],每层拉筋的初始长度L0i=Lbi+Lai,由式(18)可得。
(16)
(17)
(18)
当拉筋在挡墙上半部分时,拉筋长度仅随拉筋垂向影响范围Syi减小而减小;处于挡墙下半部分时,拉筋长度的变化包括随破裂面变化的无效长度和随Syi减小的锚固长度2部分。而拉筋的长度存在1个最优值,拉筋并不是越长越好,应综合考虑包括安全性、实用性、经济性等各方面因素来选择最佳拉筋长度[16]。因此,基于极限稳定状态,用筋面积最少的原则,需通过试验对L0i进行折减,得出最佳拉筋长度。同时,为了材料制作以及施工方便,可将长度相近的相邻层拉筋设置为等长度。
3试验设计
3.1试验材料
模型箱体材料侧板为1.5 cm厚胶合板,底板厚度为2 cm厚胶合板,净空间尺寸长73.5 cm、宽47 cm、高48 cm,如图6所示。

图6 模型箱Fig.6 Model box
挡墙面板采用150 g标准双胶纸作为墙面板,平面尺寸50 cm×50 cm,试验中需对墙面纸板进行折叠,两侧向后折叠1.5 cm,底部折叠2.0 cm。折叠后实际尺寸宽47 cm、高48 cm。
填料为干燥的洁净粗砂(石英砂),填砂重度γ=15.81 kN/m3,由直剪试验得抗剪强度指标c≈0,φ=34.8°。砂土的颗粒级配曲线如图7所示。干砂的密实度对于筋材拉力和筋材与砂间的摩阻力发挥十分关键,但夯实一定程度后压密作用不明显,密实度不会一直增加[17]。因此,为了排除填土密实度对拉筋布置方式的影响,试验过程中将统一用胶锤捶打垫板对砂土进行夯实,直至砂土无明显下沉。

图7 颗粒级配曲线Fig.7 Gradation curve of grain size
加筋材料为信封用100 g无纹牛皮纸,抗拉试验测得宽0.5 cm的筋带抗拉力[σ]=20.62 N。与填砂之间的摩擦系数f=1.16。
3.2模型填筑步骤
裁剪拉筋和墙面板,将拉筋用胶带粘贴到墙面板内侧;将可拆卸挡板固定在模型箱侧板上,粘贴有拉筋的墙面板紧贴可拆卸挡板内侧放置;向模型箱内分层填入填砂,每层统一用胶锤捶打垫板对砂土进行夯实,同时整平,铺入相应层拉筋,直至试验箱顶,完成填筑;撤去可拆卸挡板、使纸质墙面板及拉筋承受土压力,完成模型。

图8 拉筋布置方案Fig.8 Schemes of reinforcement arrangement
4试验数据及分析
4.1合理拉筋间距试验
为避免其他因素的干扰,探究合力的拉筋间距布置规律,统一取筋带宽度0.5 cm,拉筋长度沿深度方向分3部分:墙面板上H/3部分取30 cm,中H/3部分取20 cm,下H/3部分取15 cm。墙面布筋层数n分别取5,6,7层,通过式(10)和式(12)初步拟定层数n下的拉筋布置间距。为方便制作模型和数据对比,对计算的拉筋布置间距进行适当调整,同时,采用每层4,5,6根拉筋等8种布筋方式进行对比。
试验中,由于拉筋长度足够长,材料强度大,挡墙基础为刚性基础,结构的失稳破坏只存在墙面板局部变形过大而导致的丧失正常使用功能的破坏形式,以此判断结构的稳定状态,若墙面板变形小,往外凸出不超过1 cm,则视为稳定状态,反之,视为失稳破坏。8种布置形式如图8所示,所得试验结果如表1所列。
极限稳定状态下,拉筋的合理布置形式为“7层×5根”,加筋密度为35根,拉筋的水平、垂直间距如图8(h)所示。将n=7代入式(9)和式(11),运用等土压应力面积法计算的拉筋垂向布置位置和水平布置间距,如表2所列。
按等土压应力面积法,单层拉筋承担的土压力Pai按式(19)计算,总土压力Pa如式(20)。

表1 拉筋布置试验结果

表2 拉筋水平、垂直间距
(19)

(20)
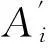
试验中,拉筋间距并未严格按照等土压应力面积法计算布置,做了一定的调整,故试验值拉筋的Syi取其上下层间距中点。8种布筋方式下Pai/Pa曲线见图9。

图9 单筋土压应力与总土压应力比值曲线Fig.9 Curves of the ratio of single-layer soilcompressive stress to total soil stress
从图9中可知,5层、6层拉筋布置疏密不合适,不符合等土压应力面积布筋,单根拉筋受力不均衡;墙体稳定下的7层布筋形式符合等土压应力面积法,布筋疏密合理,筋带受力均衡,墙面板平整度最好。稳定的7层布筋形式下每层拉筋承担的土压应力逐渐趋于等值,但考虑填土体与模型箱的边界摩擦作用和墙体顶部拉筋与填土摩擦力不足的影响,第一层拉筋间距可在理论值基础上适当减小,底部的拉筋间距可适当增大。
4.2筋带宽度试验
采用图8(h)所示的合理布置间距和拉筋长度,取筋带的宽度分别为0.5,0.4,0.3 cm(低于0.3 cm的筋带制作困难)进行试验,试验结果如表3所列。试验得出,墙面板按照“7层×5根”布筋方式,3种宽度的筋带均能保持稳定,而0.3 cm用筋量最小,较0.5 cm节约了40%,较0.4 cm节约了25%。

表3 筋带宽度试验结果
4.3拉筋长度试验
采用“7层×5根”的拉筋布置方式,取0.5,0.4,0.3 cm 3种筋带宽度,初始长度如图8(h)所示长度布置形式,分别取α=1,0.8,0.7,0.6,0.5进行拉筋长度折减。试验中,结构的破坏形式只存在由于拉筋过短的墙面板 “整体倾覆”破坏。不同长度的布置方案如图10所示,试验结果见表4。

图10 拉筋长度布置方案

拉筋长度筋带宽0.5cm筋带宽0.4cm筋带宽0.3cm用筋面积/cm2结构状态用筋面积/cm2结构状态用筋面积/cm2结构状态1.0li362.0稳定290.0稳定217.0稳定0.8li290.0稳定232.0稳定174.0稳定0.7li253.0稳定203.0稳定152.3稳定0.6li217.5稳定175.0破坏130.5破坏0.5li181.3破坏145.0破坏108.8破坏
极限稳定状态下,筋带宽度0.3 cm的最短筋带长度为0.7li,用筋面积152.3 cm2,较0.4 cm宽度下筋带长度为0.7li的用筋面积少25%,较0.5 cm宽度下筋带长度为0.6li的用筋面积少30%。布置方式相同时,墙体的稳定性取决于拉筋的有效锚固面积,宽筋的拉筋长度可适当较短布置,窄筋可相应较长布置,但窄筋较宽筋的无效加筋面积少,经济性好。
4.4拉筋布置方式的对比试验
一般而言,沿整个挡墙高度上拉筋等长布置。为探讨“上长下短”及“上下等长”2种拉筋随埋深的布置类型的优劣,取筋带长度系数 、筋带宽度0.5 cm、图8(h)所示的“上下等长”布置方式与相同用筋面积、筋带宽度、拉筋布置间距的“上下等长”布置方式进行试验对比,“上下等长”布置方式如图11所示。

图11 拉筋等长布置方案Fig.11 Scheme of equal length
筋带“上长下短”布置方式的用筋面积为217.5 cm2,拉筋总根数m=35根,换算为“上下等长”布置方式的筋长l=S/(ma)=12.4cm。
“上下等长”布置的墙面板呈现筋带被拔出的失稳破坏现象,而 “上长下短”模型稳定。
5结论
通过砂箱加筋土挡墙模型试验,进行了关于拉筋间距、筋带宽度和拉筋长度的合理布置方式分析,得出以下结论:
(1) 根据加筋土挡墙结构特点,为实现墙面板土压力与拉筋拉力的平衡、拉筋拉力与填土摩擦锚固的稳定,提出了“等土压应力面积法”的拉筋均匀化受力布置原则,推导了土压力三角形分布模式下使拉筋均能充分发挥强度的墙面拉筋间距比计算式,是对传统“等间距”布筋方式的合理改进。
(2) 砂箱模型试验表明,基于等土压应力面积法布筋原则,采用与土压力沿深度逐渐增大相适应的拉筋“上疏下密”布置形式可实现筋带均衡受力,在“窄筋密布”的条件下具有更好的稳定性且用筋量更少。
(3) 加筋土挡墙的稳定性主要取决于穿过滑动土体锚固于稳定区域的筋带面积,在总筋带面积相等条件下,与墙后填土潜在破裂楔体呈上宽下窄形状相适应的筋带“上长下短”布置方式稳定性优于“上下等长”布置,更能均衡地沿墙高提供拉筋锚固力,与等土压应力面积法布筋原则相一致。
(4) 同等用筋量时,采用“窄筋长布”的方式较“宽筋短布”能增加筋带有效锚固面积,提高挡墙稳定性;相同稳定状态下,“窄筋”在滑动区无效面积较“宽筋”少,总用筋量小,有较好的经济性。
参考文献:
[1]VIDAL H. The Principle of Reinforced Earth[J]. Highway Research Record, 1969, 282: 1-16.
[2]何光春,周世良. 加筋土技术的应用及进展 [J]. 重庆建筑大学学报,2001,23(5):11-15.
[3]欧阳仲春. 现代土工加筋技术[M]. 北京:人民交通出版社,1991.
[4]杨广庆. 加筋挡土墙合理设计方法的探讨[J].长江科学院院报,2014,31(3):11-18.
[5]杨锡武,易志坚. 基于离心模型试验和断裂理论的加筋边坡合理布筋方式研究[J]. 土木工程学报,2002,35(4):59-64.
[6]雷胜友,陈辉. 不同筋材和布筋形式对加筋土强度影响的试验研究[J]. 西南大学学报(自然科学版),2013,35(8):122-127.
[7]张孟喜. 加筋土挡墙合理布筋方向的有限元分析与试验验证[J]. 公路,1993(5):42-46.
[8]王初生,王园,唐辉明. 土工织物加筋柔性桥台合理间距的模型试验对比研究[J]. 公路交通科技,2004,21(5):36-38.
[9]包承纲,汪明远,丁金华. 格栅加筋土工作机理的试验研究[J]. 长江科学院院报,2013,30(1):34-41.
[10]BILGIN O, MANSOUR E. Effect of Reinforcement Type on the Design Reinforcement Length of Mechanically Stabilized Earth Walls[J]. Engineering Structures, 2014, 59: 663-673.
[11]TB10025—2006,铁路路基支挡结构设计规范[S]. 北京:中国铁道出版社,2006.
[12]陈忠达,原喜忠. 路基支挡工程 [M]. 北京:人民交通出版社,2013.
[13]刘成宇. 土力学[M]. 北京:中国铁道出版社,2010.
[14]严驰,张书杰,徐奉池,等. 土工合成材料界面作用特性研究[J]. 石油工程建设,2007,33(6):11-15.
[15]张师德,吴邦颖. 加筋土结构原理及应用[M]. 北京:中国铁道出版社,1986.
[16]贺会团.加筋挡土墙关键技术研究[D]. 南京:南京水利科学研究院,2007.
[17]叶观宝,张振,徐超. 加筋土挡墙模型试验研究[J]. 勘察科学技术,2010(2):3-5.
(编辑:曾小汉)
Discussion on Rational Reinforcement Layout of Reinforced SoilRetaining Wall Based on Sand Box Model Test
ZHANG Yu-guang1,2, LUO Qiang1,2, ZHANG Liang1,2, JIANG Liang-wei1,2, TAN Xiao-ying1,2
(1.MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu610031, China; 2.School of Civil Engineering, Southwest Jiaotong University, Chengdu610031, China)
Abstract:The rational layout of reinforcement in reinforced soil retaining wall is discussed by using sand box model test. The horizontal and vertical spacings, width and length of reinforcement in the prerequisite of minimum reinforcement area under limit stable state are researched. According to the method of equal soil pressure, the layout of reinforcement which is increasingly denser in vertical direction with equal horizontal spacing is put forward, and the corresponding calculation formula is presented. Analysis shows that the layout pattern “sparse in the upper part and dense in the lower part” which is consistent with the increasing soil pressure along depth leads to a balanced force on the reinforcement, and this layout pattern (narrow geobelts distributed densely) requires less amount of reinforcement and achieves better stability; while the layout with long geobelts in the upper part and short geobelts downwards which adapts to the shape of backfill potential rupture wedge (wide in the upper part and narrow in the lower part) is prior to the layout with geobelts of equal length; and moreover, narrow and long geobelts could increase the effective anchorage area and improve the stability of retaining wall compared with wide and short geobelts.
Key words:reinforced soil retaining wall; sand box model; reasonable distribution of reinforcement; equal stress area method;potential rupture surface
中图分类号:TU43
文献标志码:A
文章编号:1001-5485(2016)05-0076-07
doi:10.11988/ckyyb.201500702016,33(05):76-82,87
作者简介:张玉广(1989-),男,贵州德江人,土家族,硕士研究生,主要从事铁路路基方面的研究,(电话)18280266884(电子信箱)421834085@qq.com。
基金项目:国家“973”计划课题(2013CB036204)
收稿日期:2015-01-12 ;修回日期:2015-03-25

