MoM法分析目标面-线-面结构的散射特性研究*

（西北工业大学电子信息学院,西安 710129）

隐身技术作为未来飞行武器设计的重要指标，一直受到世界各军事大国的高度重视。目前我国虽然在隐身飞行武器方面做了大量专题研究，但是隐身技术应用方面还处于起步阶段，主要集中于型号工程前期研究，尚无正式装备的隐身飞行武器。在总体设计、隐身/气动综合优化、吸收材料、测试技术等方面仍存在较大差距[1]。为了设计出隐身性能良好的武器装备系统，设计工程师在设计飞行武器结构时，常常采用面-线-面连接结构，通过对目标结构进行合理设计，可以在一定角域内显著减小雷达散射截面积（RCS），从而达到隐身目的。

由电磁理论可知，目标面-线-面结构中导线连接理想散射导体，改变了散射体的边界条件，从而改变了目标表面电流分布，进而使得目标本身的RCS值也随之变化[2]。即导线的引入使得飞行目标的电磁散射特性发生变化。要提高目标的隐身性能，只有将整个结构进行一体化分析，才能得出其准确的电磁特性。对于包含面-线-面连接结构的军事目标的电磁散射特性计算，本文采用基于电场积分方程的矩量法（EFIE-MoM）对该问题加以分析。

EFIE-MoM方法以电流为基础，通过求解出表面电流求解散射场[3]。求解目标表面电流需要计算分布在目标表面所有的未知量，因此当用MOM法求解边界积分方程时，基函数的选取显得尤为重要。对于如线-线、线-面、面-面等复杂连接问题，单一的基函数已无法满足连接区域的电流连续这一重要边界条件。近年来已有很多学者尝试结合不同基函数及边界条件去解决这一问题：文献[4]针对线-面连接问题，对于纯导线和导体面区域，采用一般的分域基函数，然而对于特殊的线-面连接处，则引入同时满足边界条件和电流连续性条件的基函数，从而求解了该线-面连接问题的积分方程；对于面-面连接问题，文献[5]则采用全域基函数来表面电流计算，但因为其使用了全域基函数，同时引入了介质分界面的不同情况，从而使得求解公式较为复杂繁琐。对于另一常见的连接问题：面-线-面连接问题，文献[6]研究了仅一个连接点的情况，而对于实际的飞行武器结构，庞大的飞行器表面需要多根导线同时工作，因此研究计算存在多个连接点的面-线-面连接结构十分必要。

本文在上述研究的基础上，通过MoM法对含有面-线-面结构的目标电磁特性进行理论计算分析，验证了导线的引入对整体结构散射特性的影响。在面-线-面连接域的处理上，本文采用模型通用的Costa基函数[7]，很好地解决了面-线-面连接处的电流不连续性，为方便准确分析出目标的隐身特性提供了基础。可以证明，此方法适用于几乎所有的细导线与任意形状散射导体目标表面相连的情形，而且算法时间复杂度和空间复杂度较小。

1 散射理论

对于散射导体目标，在入射平面电磁波的照射下，其表面S会产生感应表面电流，这里S通常指目标所有散射导体面与所有导线的组合。这些表面电流就是二次辐射源，向空间各点产生散射效应，通过干涉（各散射点的矢量叠加）在空间某点形成确定的电场，这也是雷达能够探测到目标的理论依据[8]。

因此，散射问题的计算首先需要求出目标在平面波照射下的感应电流，感应电流与入射电磁场相互作用，引起空间电磁场分布的改变。因此，目标散射问题求解过程的核心即是：在给定的平面波照射下，采用精确解解析、数值方法或近似方法求解目标上的感应电流密度。本文采用数值方法MoM法对目标结构表面电流分布进行分析求解。

2 MoM法分析面-线-面结构散射特性

2.1 电场积分方程

当入射平面电磁波照射到导体目标上时，目标表面要产生感应电流J(r)，该感应电流进而在自由空间进行辐射形成散射场。将等效电流J(r)代入电场积分方程[9]，如式（1）所示，可以计算散射导体目标的散射电场和磁场。

式中，A(r)为磁矢量位函数，Φ(r)为标量电位函数。它们的表达式分别如式（2）和式（3）所示：

式中，为真空磁导率，为真空介电常数，为入射波的角频率，为三维自由空间的标量Green函数，其中k0为传播常数，为源点到场点的距离。

2.2 基函数

为了获得目标中面-线-面连接结构的矩量解，首先将该目标结构的导体表面及导线离散化：导体表面被剖分为三角面元，这样可以简单有效地刻画出导体表面的局部精细特征；细导线结构采用直接的线元剖分。矩量法的一个关键步骤是基函数的选取。面-线-面连接结构共选定3组分域基函数，即导体基函数、导线基函数以及连接域基函数。连接域即连接点的周边区域。

理想散射导体表面采用三角形面元剖分并选用广泛使用的RWG基函数[10]，(r)代表这组基函数，为导体i的第n个基函数。细导线采用线元剖分和线状结构常用的脉冲基函数[11]，(r)代表这组基函数，其含义为导线j的第n个基函数。连接域基函数fk(r)表示面元与线元第k个连接点的基函数。对于任意理想散射导体与细导线的面-线-面结构，假设导体个数为Nb，第i个导体的三角面元之公共边的个数为NBi；线元的节点数目为Nw；三角面元与线元的交叉点个数为Nj。则此结构上的电流分布可展开为式（4）所示。

式中，为未知系数。

为了获得军事目标准确的散射场特性，必须着重处理好面-线-面连接处电流的不连续性。面-线-面连接结构中最重要的问题即是处理好三角面元与线元的连接点。对于任意几何结构上的连接处区域，其连接点处的基函数应具备的变化规律。这种面-线-面的第k个连接域基函数fk(r)可具体分为两部分加以研究：第一部分是关于细线的部分（与连接点相连线段的前半段），第二部分则是关于连接点附近的散射导体面部分[7]，如图1所示。

图1 连接点的基函数Fig.1 Basis function of the connected points

式中，是与连接点k有关的三角形顶角的和，用来保持与线元部分的电流连续。以平板结构中间部分为例，其值就是2π。η为面积坐标，和r0分别表示三角形面元内的任意一点和与其相连接点的坐标。对于连接点周围的某三角形，如图2所示，若选取顶点2为连接点，则，其中/是整个三角形的面积，A则为三角形面元内的任意点r与顶点1、3组成的面积。

式（5）中在导线上的表达式为：

式中，表示从连接点到连接段中点处的单位矢量，且

式中，s代表导线沿轴向的长度，即在连接点处，如图1所示。

这样，由于每个连接点在其所连接的散射导体与导线两个部分的基函数表达方式不同，同时每个连接点仅有一个未知数，且与连接点周围三角形的个数无关，使得算法时间复杂度和空间复杂度得到很大程度上降低。

通过对式（5）的求解，连接域k的电荷密度如式（9）所示：

可证明，连接域 所包含的导体部分电荷量为1，所包含的导线半段上的电荷量为-1，因此每块连接域总电荷量为零，从而说明引入Costa基函数很好地解决了目标结构中连接点处电流不连续问题。

2.3 矩阵方程

图2 连接点周围的三角形Fig.2 Triangles around the connected points

在积分方程和基函数确定后，即可应用矩量法进行求解。应用MoM法中常用的检验方法伽辽金（Galerkin）法[12]，将式（4）代入式（2）、式（3）并对式（1）作检验，遵循矩量法的求解步骤，可得矩阵方程式（10）。式（10）中，Z为阻抗矩阵，由分别表示三角面元及线元的自作用及相互作用的九个子矩阵组成。因为Z表示多个散射导体的阻抗矩阵，因此式（10）中的每个子矩阵又分别由许多子矩阵构成。

式中，表示维数为Nm×Nn的子矩阵（m、n可表示B、W、J），其中

式中，NB、NW和NJ分别表示理想散射导体、理想导线和连接点总的未知电流数数目；NBi、NWj分别表示理想导体i中和理想导线j中的未知数数目；Nb、Nw和Nj分别表示散射导体、理想导线和连接点的数目。

在式（10）中，对于电流列向量有：

类似的，对于电压列向量有：

求解矩阵方程式（10），即可得到面电流、线电流及面元和线元之交叉点处电流的展开系数，从而获得目标面-线-面连接结构的电流分布，进而由RCS定义式可计算出连接结构的散射场。

3 验证实例

为了说明本文算法的正确性，利用上一节介绍的MoM法及所选定的基函数，对理想面-线-面连接结构的RCS值进行了Matlab编程计算。隐身结构中，为了对比导线连接分形散射体对目标整体散射特性的影响，程序计算了未经细导线连接的面-面结构和经细导线连接的面-线-面连接结构的RCS值。同时本文使用HFSS电磁仿真软件对面-线-面结构进行仿真计算，通过对比验证文中所述方法及所编程序的正确性。

图3是基于HFSS软件的面-面结构和面-线-面结构的表面电流矢量分布显示图。设定入射波为频率1GHz沿Z负半轴入射的单位平面波，极化方向为x轴。理想散射导体的尺寸均为 （λ/4）×（λ/4）（λ为入射波的工作波长），模型均放置在xoy平面内。图3（b）结构中细导线长度l=λ/4 。

由麦克斯韦方程组可知，分形散射体经细导线连接后，其边界条件发生改变，同时由于导线的引入改变了整个结构的相位，使得结构的表面电流分布发生了明显的变化，如图3所示。

图3 基于HFSS的两种结构表面电流矢量分布图Fig.3 Distribution profiles of two kinds of structure surface current vector

在Matlab编程计算中，图3（a）的模型中只有两个散射导体平面，没有细导线和连接域，因此计算中不用考虑导线部分和连接域问题，仅对散射导体平面进行三角面元剖分，采用RWG基函数进行Galerkin检验后计算矩阵方程，获得RCS值。图3（b）的模型中有两个散射导体、一根细导线和两个连接域，按照上一节的分析步骤进而计算出RCS值。

当雷达接收机方位角phi= 0°时，利用HFSS软件对面-面结构和面-线-面连接结构的RCS值进行运行绘制，其数值随俯仰角theta的变化曲线如图4所示。

由图4中两条曲线可以看出，后向RCS变化约15dB，从而证明了细导线引入对目标散射特性的影响。同时，由于该结构的对称性，RCS减缩作用也呈现相应的对称性。其中，导线对目标散射特性的影响程度与平面入射波的频率、极化、入射方式及散射体的形状、尺寸、连接方式有直接关系。

图5是对未经导线连接的面-面结构运用MoM法计算的RCS与HFSS软件仿真结果的比对，图6是对经导线连接的面-线-面结构运用MoM法计算的RCS与HFSS软件仿真结果的比对。

由图5和图6对比曲线可以看出，采用本文选定的MoM方法计算的RCS值与HFSS仿真结果基本吻合，从而验证了文中方法在包含面-线-面结构的目标散射特性分析计算中的有效性与正确性。这里需指出的是，虽然本文仅对矩形导体板面-线-面结构进行了例证，但其方法同样适用于其他任意形状的导体板及导线连接结构。

图4 基于HFSS的两种结构RCS值仿真比较Fig. 4 RCS results of two structures shown in Fig.3 simulated by HFSS

图5 MoM法计算与HFSS仿真结果比对（面-面结构）Fig.5 Comparison of RCS results obtained using MoM and HFSS,respectively (for surface-surface structure)

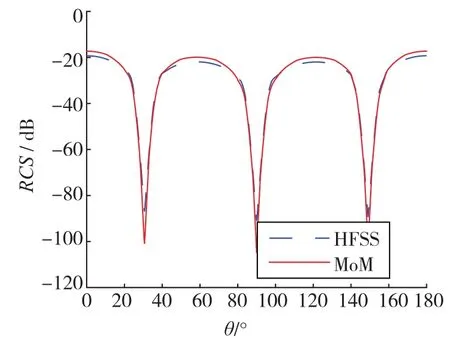
图6 MoM法计算与HFSS仿真结果比对（面-线-面连接结构）Fig.6 Comparison of RCS results obtained using MoM and HFSS,respectively (for surface-line-surface structure)

4 结束语

本文采用MoM方法分析隐身目标面-线-面结构的散射特性，不仅简单而且有效。同时，本文介绍了一种适合连接域的基函数，可以很好地解决连接处电流不连续问题。通过实例的Matlab编程计算与HFSS仿真结果比对不难看出，经细导线连接后的面-线-面结构散射体RCS值发生了变化。同时，计算结果验证了本文方法在面-线-面结构散射场计算中的正确性。

研究复杂结构目标表面的散射特性，对目标的高性能隐身设计有着深远的参考意义。本文所提出的方法为后续探索结构的单元尺寸、间距、连接方式给出了有力的技术支撑。

[1] 桑建华, 周海, 陈颖闻. 隐身技术推动新一代飞行器发展 [J].航空科学技术, 2012(3)：15-18.SANG Jianhua, ZHOU Tao, CHEN Yingwen. Development of new generation air vehicles driven by stealth technology[J]. Aeronautical Science and Technology, 2012(3)：15-18.

[2] 聂在平.目标与环境电磁散射特性建模--理论、方法与实现(基础篇)[M].北京：国防工业出版社, 2009.NIE Zaiping. Model for electromagnetic scattering characteristics of targets and environment -- theory, method and realization (foundation)[M].Beijing： National Defence Industry Press, 2009.

[3] 哈林顿. 计算电磁场的矩量法[M]. 王尔杰,译. 北京： 国防工业出版社, 1981.HARRINGTON R F. Field computation by moment methods[M].WANG Erjie translated. Beijing： National Defence Industry Press, 1981.

[4] HWU S U, WILTON D R. Electromagnetic scattering and radiation by arbitrary configurations of conducting bodies and wires[R].Applied Electromagnetics Laboratory, University of Houston, Houston,1989.

[5] KOLUNDZIJA B M. Electromagnetic modeling of compo-site metallic and dielectric structures [J]. IEEE Trans Microwave Theory and Tec, 1999, 47(7)：1021-1032.

[6] 万继响, 张玉, 梁昌洪. 任意导体与天线连接问题的MoM分析[J]. 电波科学学报, 2003,18(5)：523-525.WAN Jixiang, ZHANG Yu, LIANG Changhong. Method of moment analysis of connect between wire antennas and arbitrary shape conductors[J]. Chinese Journal of Radio Science, 2003, 18(5)： 523-525.

[7] COSTA M F, HARRINGTON R F. Minimization of radiation from computer system：Int. Elect. Electron[C]. Conference and Exposition Proc.1983：660-665.

[8] 王宇桢.复杂目标RCS计算[D]. 西安：西安电子科技大学,2008.WANG Yuzhen.RCS Calculation of Complex Targets[D].Xi’an：Xidian University, 2008.

[9] 段洪.任意形状目标电磁特性的矩量法研究[D]. 西安：西北工业大学, 2010.DUAN Hong.Method of moment research of electromagnetic characteristics of arbitrary shape objects[D].Xi’an： Northwestern Polytechnical University, 2010.

[10] 王兴,龚书喜,王文涛,等.一种快速分析面面结构电磁辐射特性算法[J].西安电子科技大学学报(自然科学版),2011,38(4)：106-111.WANG Xing, GONG Shuxi, WANG Wentao, Z Yujie. Fast analysis of electromagnetic properties of surface/surface configurations[J]. Journal of Xidian University, 2011, 38(4)：106-111.

[11] AN Xiang, L Zhiqing. An IE-FFT based Hybrid method for analyzing wire surface configurations on electrically large platforms[J].Microwave and Optical Technology Letters, 2009, 51(2)：409-418.

[12] RAO S M, WILTON D R , GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Trans on Antennas and Propagation, 1982, 30(3)：486-490.