基于等效板的含离散源损伤机翼结构分析*

（中国民航大学天津市民用航空器适航与维修重点实验室，天津 300300)

机翼和机身结构的安全性直接关系到飞机的安全，因此相关的飞机设计规范或适航条例对机翼机身结构的安全性均有明确的规定，其中一个重要的内容就是要求机翼和机身结构在带有离散源损伤的情况下, 保证安全飞行[1]。因机翼和机身结构复杂，设计难度大，而等效方法提出一种简单的方案或设想，使某些特性和规律等方面的性能和指标相同，即真实结构与等效模型之间的某些特性可以彼此互换，而分析结论一致，从而通过简化使问题化繁为简，快速得到解决办法。因此，简化部分机翼结构，使用等效设计方法建立精确的机翼结构模型，对于快速有效的分析机翼特性具有重要作用。

本文把压缩载荷作用下的含离散源损伤加筋板模型作为机翼结构[2]，采用Nastran优化设计方法，使优化设计之后的含离散源损伤不加筋板模型的静、动力学特性和含离散源损伤加筋板模型的静、动力学特性达到等效，从而使优化设计之后的不加筋板模型与机翼结构是等效结构，进而在等效模型上展开进一步分析和研究。这对于快速、有效的分析含离散源损伤机翼结构的力学特性具有重要作用。

1 离散源损伤初始模型建立

为研究含离散源损伤机翼结构的静、动力学特性，建立含离散源损伤不加筋板模型并作为初始模型；建立含离散源损伤加筋板模型即机翼结构模型并作为目标模型。使优化设计之后的初始模型和目标模型的静、动力学特性达到等效。含离散源损伤加筋板模型试件的几何尺寸如图1所示。

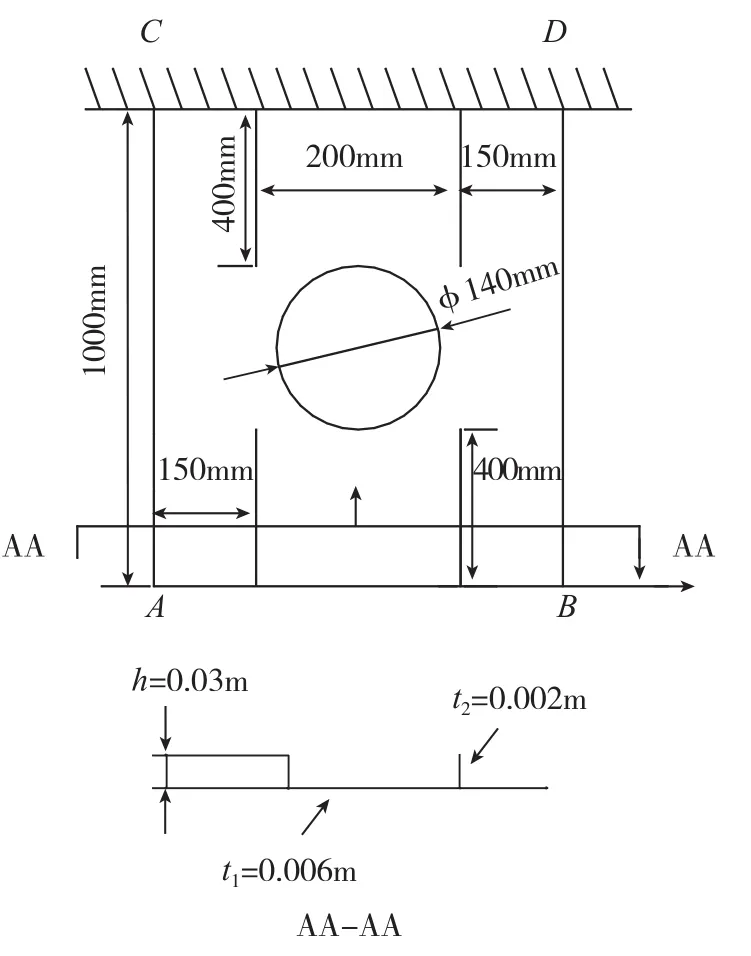
图1 含离散源损伤加筋板几何参数Fig. 1 Geometric parameters of stiffened plate with discrete source damage

模型均采用薄铝板材料，具体材料参数如表1所示。

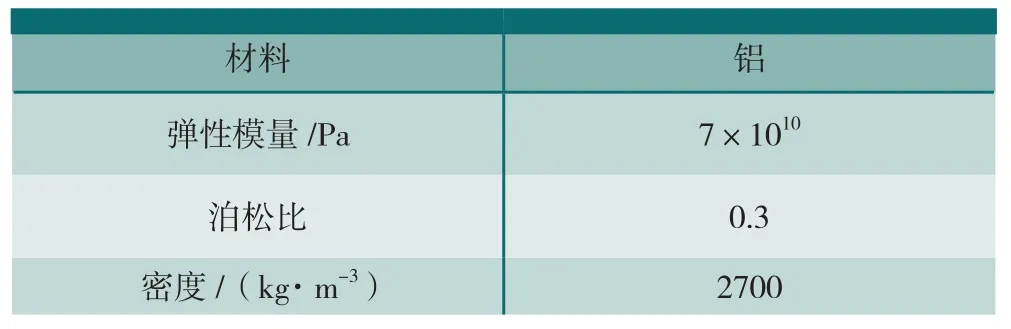
表1 材料参数

目标模型和初始模型的离散源损伤位置和几何尺寸相同，平面厚度相同且都不穿过两侧加强筋位置，具体如图2所示。

两个板模型的网格划分方向和大小相同，为得到更精确的计算结果，在离散源损伤周围对网格采取加密精细化处理。因为本文优化设计分析过程仅在线性范围内展开，因此对初始模型进行预加载仿真分析，确保优化设计过程不出现非线性变化等因素的影响。

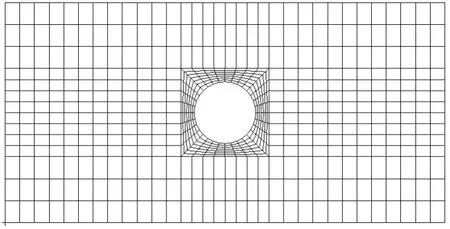
图2 含离散源损伤不加筋板模型Fig.2 Unstiffened plate model with discrete sources damage

通过PATRAN有限元分析可知，其自由端Z向变形位移和最大应力水平如图3、图4所示：

在对初始模型的仿真分析中，由分析结果可知：节点最大变形位移的百分比函数是7.99%，安全系数0.0615＜ns，均符合相关的国家技术标准[3]要求。因此，初始模型符合小变形要求和强度理论要求，后续的优化设计过程不会出现非线性等问题。

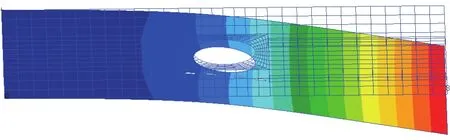
图3 最大变形位移图Fig.3 The biggest deformation displacement diagram

图4 最大应力图Fig.4 The biggest stress diagram

2 Nastran优化设计原理

Nastran优化设计程序基本原理[4]如下：

寻找一组合适的设计变量：

{x}={x1,x2,...xn}，

使目标函数的值达到最小：

minimize=F(x)，

满足约束条件：

区间约束条件：XLi≤Xi≤XUii=1,2...n,n，

不等式约束条件：Gj(x)≤0j=1,2,...,L，

等式约束条件：

Hk(x)=0k=1,2,...,k，

Nastran求解器对于优化设计,设置了3种优化算法。其中第3种方法是3种算法的核心，也是默认的优化算法[5]。

其中为第k+1次迭代的搜索方向，是满足条件θj和可行条件为标量的步长值。Nastran软件对可行性方向阀的主要改进在于：在约束边界条件上，搜索方向的选择是下面这个子优化分析问题的解：

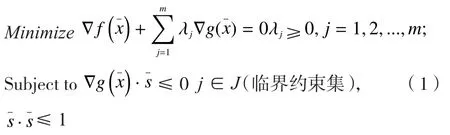
通过以上约束方程得到的搜索方向s紧贴着临界约束的边界移动，使目标函数逐渐下降。自动迭代运算直至出现最优结果，则停止计算。

3 静力学等效分析

基于Nastran优化设计原理展开对初始模型的优化设计分析，在静力学特性的基础上，通过优化设计计算，建立与目标模型静力学特性一致的静力学等效模型，若达到等效，则称优化设计之后的不加筋板模型为静力学等效模型。

设计变量：设计变量取板的厚度，设置如图5所示。通过优化T1、T2、T3三部分板厚，使初始模型与目标模型的静力学特性相同。初始厚度设置均为0.006m。

图5 优化设计变量Fig.5 Optimization of the design variables

优化设计的目标函数：

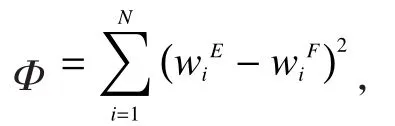
式中，N是板模型的节点数量；wiE是优化设计之后板模型第i节点位移；wiF是与优化设计之后板模型第i节点相对应的目标模型第i节点的变形位移[6]。

将包含初始模型几何尺寸、设计变量、目标函数等参数组成的优化设计程序提交Nastran求解器SOL200迭代计算[7]，设计变量T的变化如表2所示。

如表2中所示，经过5次迭代运算，找到了使目标函数Φ趋于最小的T值。把厚度最优的设计变量数值分别赋予T1、T2、T3，在Patran中重构初始模型并进行计算分析。验证优化设计后的不加筋板模型与目标模型之间各对应节点变形位移和模态频率是否相同。

本文选取图5的静力优化后不加筋板模型和目标模型互相对应的15个节点的变形位移作对比分析，此15个节点均为同一平面直线上最大的位移变形节点。验证对比如表3所示。频率结果对比如表4所示。

表3中，分别赋予优化迭代计算后的3个板厚值T之后，静力学优化设计后的不加筋板模型各节点变形位移与目标模型对应各节点变形位移数值基本相同，静力学特性基本达到等效，可称此优化设计后的模型为静力学等效模型，即建立了静力学等效。表4中的动力学特性模态频率方面，静力学等效模型和目标模型之间的模态频率仍相差较大，静力学等效模型在动力学方面的等效性则较差。因此，需要在静力学等效的基础上，继续展开对静力学等效模型的模态频率特性作进一步优化分析。

表2 静力学优化设计变量变化m

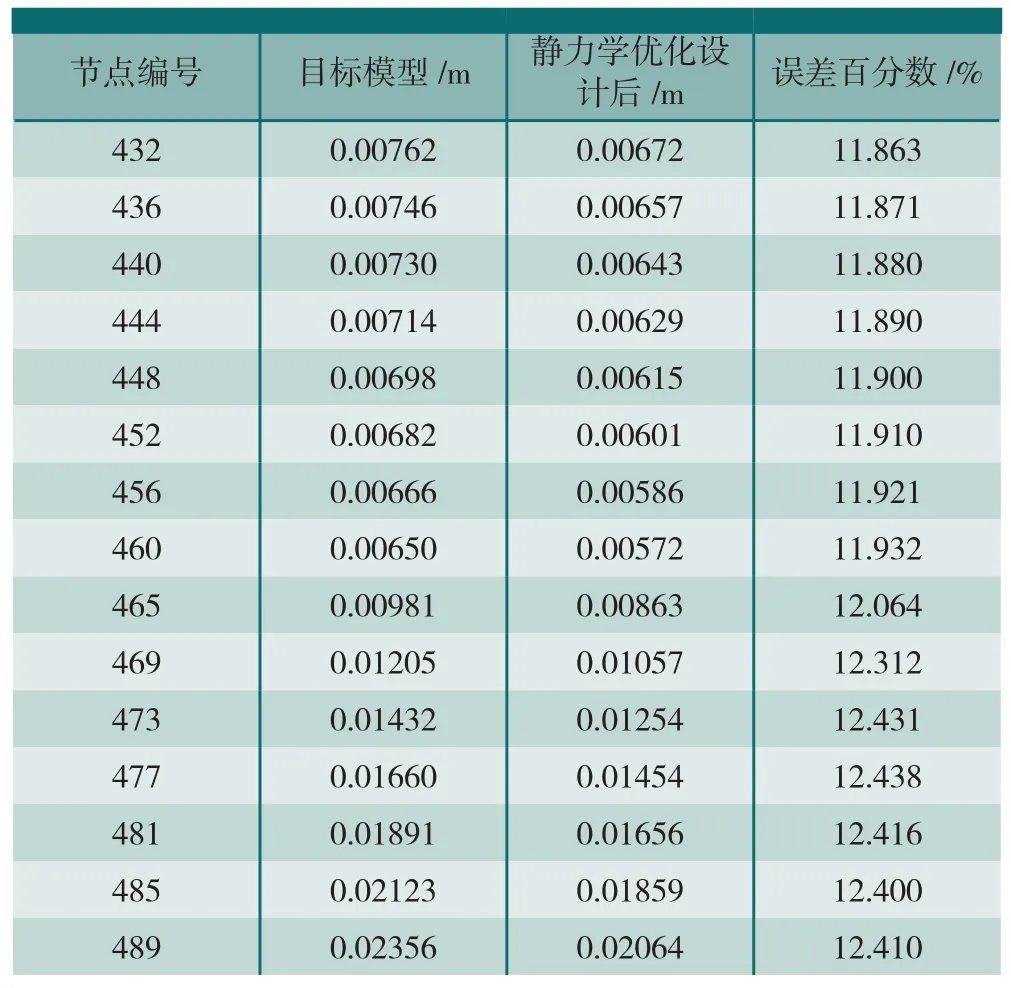
表3 静力学优化设计变形位移对比

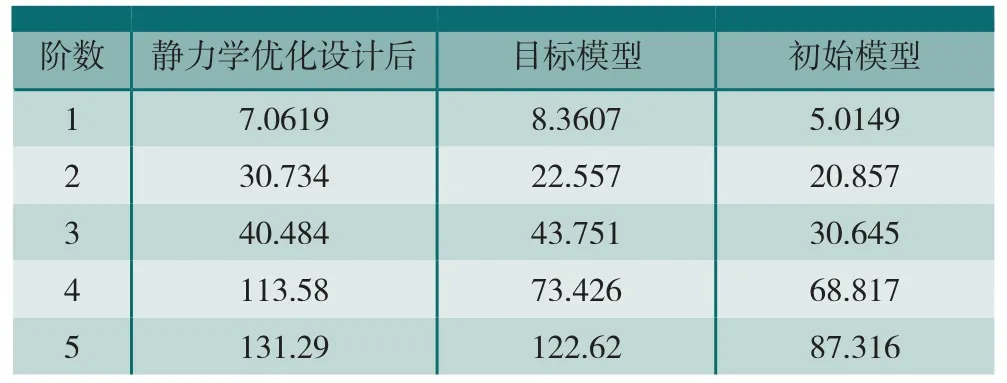
表4 静力学优化设计模态频率对比Hz

4 动力学等效分析

在静力学等效模型和目标模型的各节点变形位移相同的基础上，同时对模态频率展开优化设计分析，从而使动力学优化设计后的不加筋板模型与目标模型的变形位移和模态频率都相同，达到静、动力学特性同时等效的目的。根据Nastran优化设计原理和动力学特性，改善优化设计程序中目标函数、响应参数和限制条件的设置。

优化设计变量：板厚变化T1、T2、T3

MPC约束：所有节点的变形位移的最小二乘最小

优化设计目标函数：

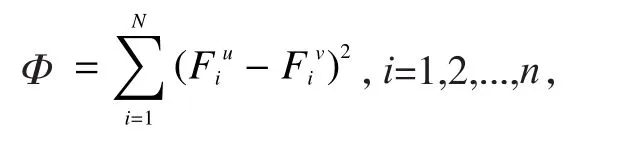
其中，N是板模型的节点数量；是目标模型的频率；动力学优化设计后板模型的频率[8]。

把修改之后的Nastran优化设计程序重新提交SOL200求解器求解计算，在静力学等效的基础上进行动力学优化设计计算。

动力学优化计算结果如表5所示。

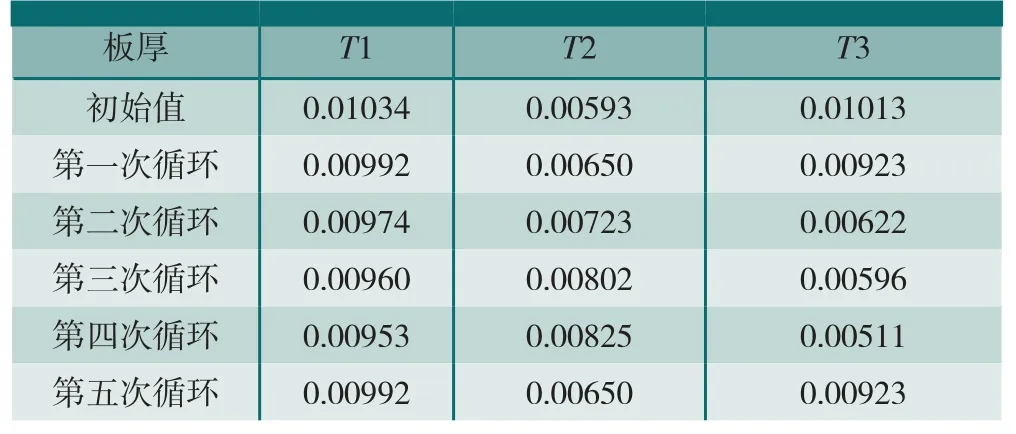
表5 动力学优化设计变量变化m

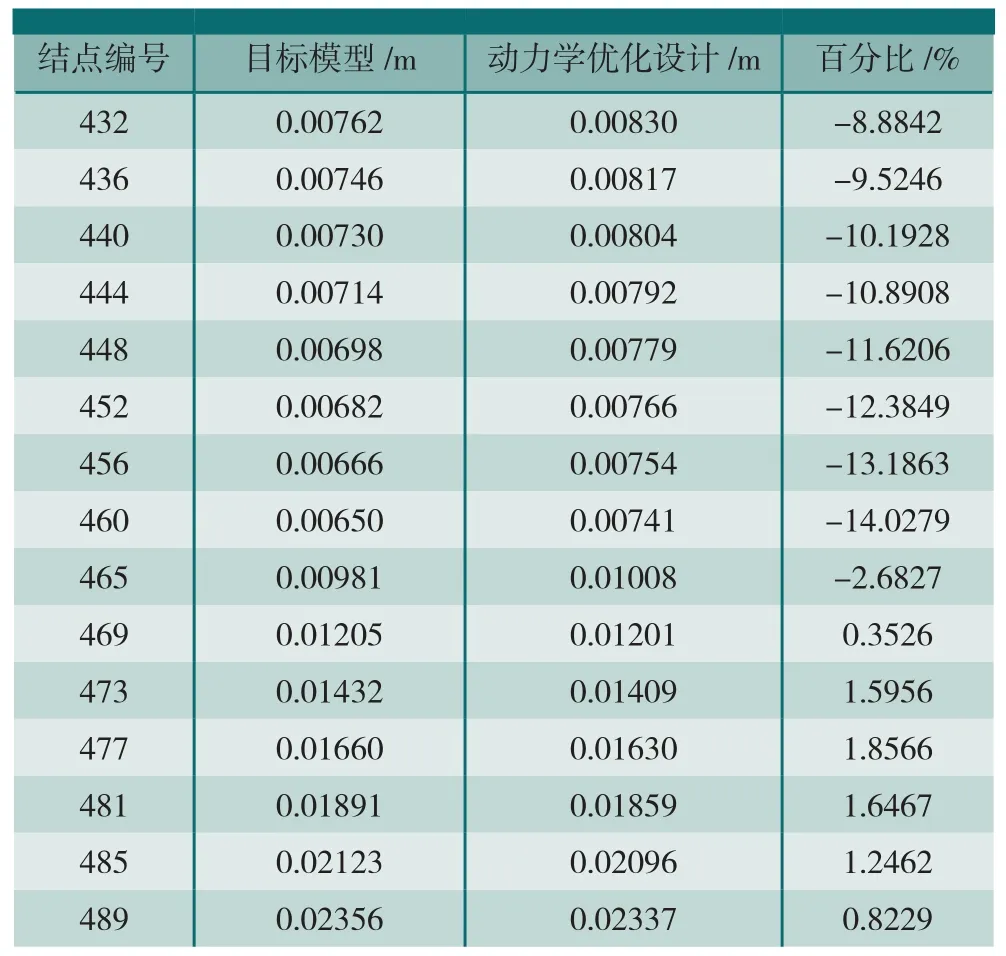
表6 动力学优化设计变形位移对比

表5中的板厚度变量T在经过5次迭代计算后，设计变量趋于稳定，目标函数Φ的最小二乘最小，目标函数取得最小值。把厚度最优的T值分别赋予板厚，在Patran仿真分析程序中对动力学优化模型进行静、动力学分析计算，提取数据文件。检验动力学优化设计后不加筋板模型节点变形位移和模态频率与目标模型各节点变形位移和频率是否相等。检验结果如表6所示。模态频率对比如表7所示。

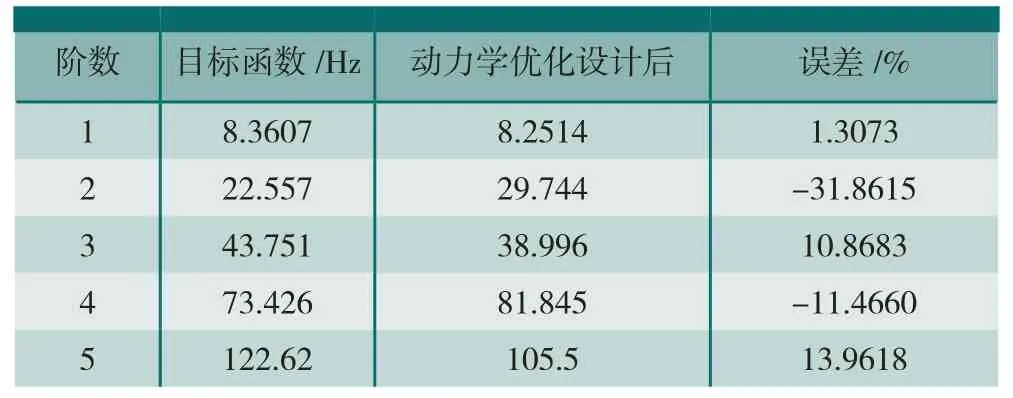
表7 动力学优化设计模态频率对比

其中，动力学优化设计板和目标模型的前3阶的弯曲和扭转振型如图6所示。

图6 有限元模型振型对比图Fig.6 Finite element model of vibration mode comparison chart

从表6、表7中可以看出，优化设计迭代计算之后，动力学优化设计后的不加筋板模型的各节点变形位移与目标模型各节点变形位移基本一致，模态频率也基本一致。静、动力学特性基本达到等效，可称此优化设计后的板模型为静、动力学等效模型。

5 算例

美国NASA兰利研究中心研发的AGARD 445.6机翼是一个国际上公认的用于在风洞中进行颤振试验的跨音速标准颤振计算模型。其试验结果可以和利用仿真分析软件计算的跨音速颤振结果进行对比验证[9]。

本文选取这一标模试验，验证Nastran动力学优化设计程序在模型等效处理上的有效性，进而分析本文编制的Nastran优化程序的有效性。

AGARD 445.6机翼翼型为NACA65A004,是具有明显跨音速气动特性的变厚度薄形机翼,展长为762mm,1/4弦线的后掠角为45°,机翼展弦比(展长与平均弦长的比值)为1.62, 机翼根稍比(翼稍与翼根部的比值)为0.66。

在Nastran优化设计程序中，图7建立的机翼模型是壳单元。AGARD 445.6机翼用匀质大的桃花芯木层合薄板制成，其二维模型如图7所示。

在Nastran优化设计程序中，图7建立的机翼模型是壳单元，AGARD 445.6机翼用匀质大的桃花芯木层合薄板制成，其具体材料参数如表8所示。

用桃花心木层合板制成的AGARD445.6机翼试验模型自然模态分布范围较宽,取前4阶计算结果。

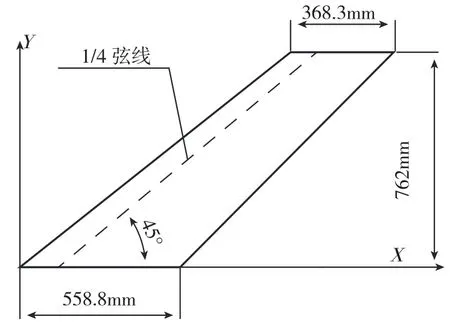
图7 AGARD 445.6 机翼二维模型Fig.7 AGARD 445.6 two-dimensional wing model

表8 AGARD 445.6机翼的材料参数

表9 AGARD 445.6机翼的固有频率表

表9为本文的计算结果与Goura[10]、Kolnay[11]、Ryan[12]计算结果和试验结果比较的数据。

AGARD 445.6机翼的固有频率比较，如表9所示。

取机翼前4阶模态的固有频率数值与Goura、Kolonay和Ryan的计算结果进行比较分析,本文的计算结果与试验值较为接近。固有模态云图如图8（a）～图10（a）所示,与文献[13]给出的模态图8（b）～图10（b）比较。

需要指出的是:图8～图11中的固有频率值是文献给出的计算参考结果,不是试验结果。所以这个值与表9中列举的值并不相同。图8中本文计算的模态图8（a）是向下,文献[13]给出图8（b）则是向上,这只是相位相差180°,振型仍然是一致的。图8～图11中振型没有相位差,本文计算的固有模态结果与文献[13]给出的模态是吻合的[14]。

图8 AGARD 445.6机翼第1阶模态对比图Fig.8 AGARD 445.6 wing for the first modal contrast

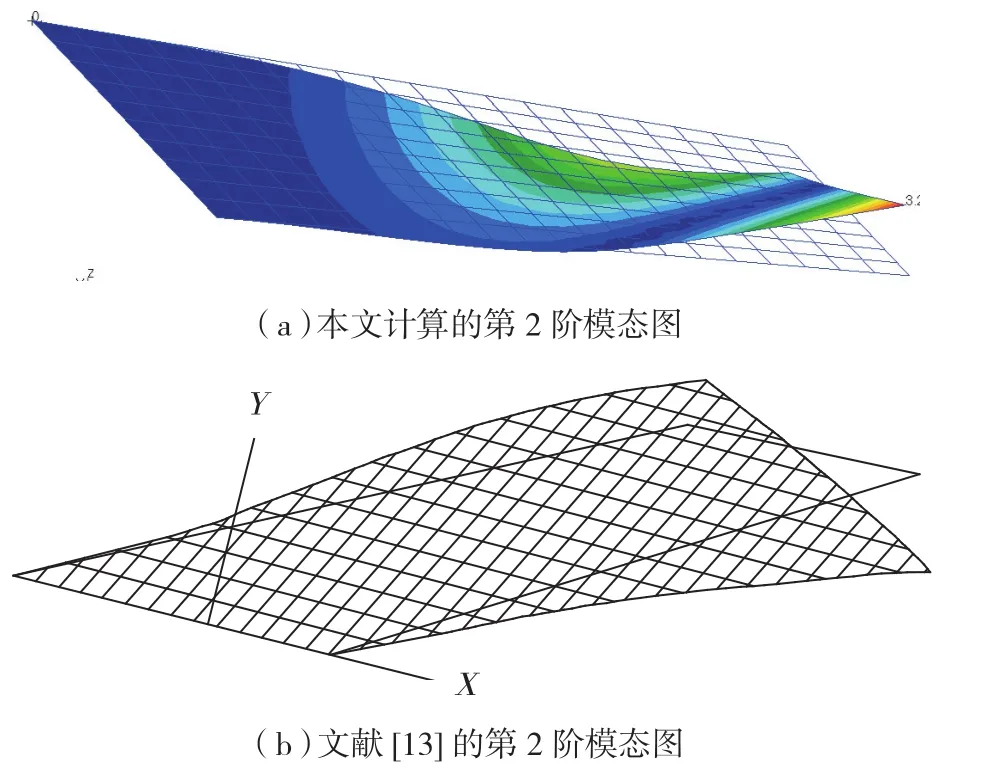
图9 AGARD 445.6机翼第2阶模态对比图Fig. 9 AGARD 445.6 wing for the second modal contrast

图10 AGARD 445.6机翼第3阶模态对比图Fig.10 AGARD 445.6 wing for the third modal contrast

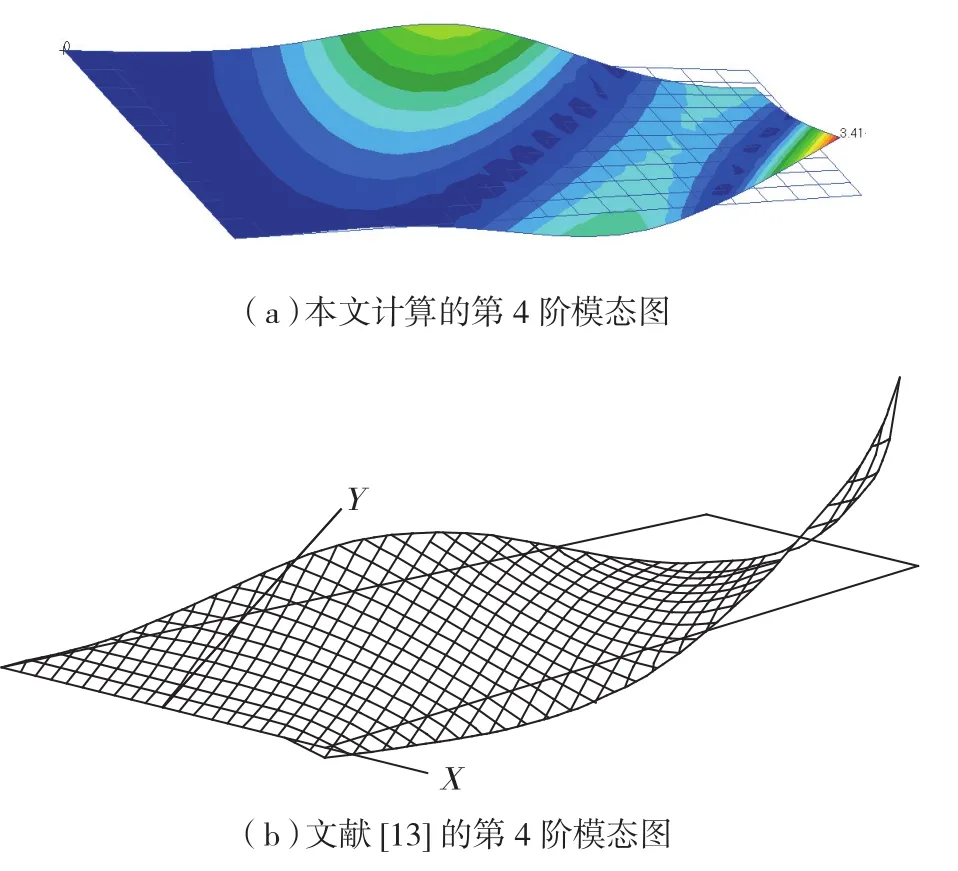
图11 AGARD 445.6机翼第4阶模态对比图Fig.11 AGARD 445.6 wing for the fourth modal contrast

6 结论

本文提出基于优化设计的等效分析方法，在针对含离散源损伤的机翼结构进行静、动力学分析的过程中，本方法只需要知道含离散源损伤的机翼结构的基本几何参数即可分析机翼结构的静、动力学特性。利用等效方法，使用参数化建模，内部自动迭代运算，计算效率高，适合于机翼结构初始设计阶段的快速建模分析。

采用本文开发的Nanstran优化设计程序对含离散源损伤机翼结构特性进行分析时，为准确对含离散源损伤机翼结构的仿真分析，要注意对约束、变量控制以及目标函数的选择和控制。

[1]杜凯，矫桂琼，王翔. 含离散源损伤复合材料加筋板的拉伸特性[J]. 复合材料学报, 2008,8:181-186.

DU Kai，JIAO Guiqiong， WANG Xiang. Tensile properties of stiffened composite panels with discretesource damage [J].Acta Materiae Compositae Sinica,2008,8:181-186.

[2]KRISHNAMURTHY T, BRIAN H. Mason.Equivalent plate analysis of aircraft wing with discrete source damage[C]// 7th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Confere,2006.AIAA 2006-2218.

[3]GB/T228.1-2010金属材料拉伸试验第1部分：室温试验方法[S].

GB/T228.1-2010 Test of metallic materials - Part 1 Tensile .RT Test Method [S].

[4]马爱军，周传月. Patran和Nastran有限元分析专业教程[M].北京：清华大学出版社, 2005.

MA AiJun，ZHOU ChuanYue. Patran and Nastran finite element analysis professional tutorial [M]. Beijing:Tsinghua University Press, 2005.

[5]程鹏. MSC/NASTRAN优化设计方法的讨论[J]. 航天器工程,1996,5: 221-225.

CHENG Peng. The MSC/NASTRAN discuss of optimization design method [J].Spacecraft Engineering,1996,5: 221-225.

[6]KRISHNAMURTHY T, Frequency response of an aircraft wing with discrete source damage using equivalent plate analysis [C]// 8th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Confere,2007, AIAA, 2007-2144.

[7]李增刚. Nastran快速入门与实例[M].北京： 国防工业出版社，2007,6：128-130.

LI ZengGang. Nastran quick start and example[M].Beijing: National Defence Industry Press，2007.

[8]KRISHNAMURTHY T.Frequencies and flutter speed estimation for damaged aircraft wing using scaled equivalent plate analysis[C]// NASA Langley Research Center, Hampton, VA 23681, U.S.A,2010.

[9]史爱明,杨永年,叶正寅. 两种跨声速气动弹性问题分析研究[J]. 空气动力学学报, 2005,23: 414-418.

SHI AiMing, YANG YongNian, YE ZhengYin. Investigation of two aeroelasticity problems in transonic flow[J]. Acta Aerodynamica Sinica,2005,23: 414-418.

[10]GOURA, LAURE G S. Time marching analysis of flutter using computational fluid dynamics[D].Glasgow: University of Glasgow, 2001.

[11]Kolonay, R. M. Unsteady aeroelastic optimization in the transonic regime [D].U S A: Purdue University,1996.

[12]RYAN J,BEAUBIEN, FRED N, et al. Time and frequency domain fluttersolutions for the AGARD 445.6 wing[R]. Ottawa:Carleton University. 2005.

[13]YATES C E,AGARD standard aeroelastie configu-rations for dynamic response - AGARD 445.6 Wing[R].1985.

[14]袁鹏程，非定常跨音速机翼的颤振分析[D]. 浙江:浙江大学, 2011.

YUAN PengCheng，Flutter analysisof unsteady transonic wing [D].Zhejiang :Zhejiang University,2011.