难加工材料切削用量可优化区间的限定

叶洪涛，王 伟，贺 芳，万 熠，刘战强

（1. 中航工业沈阳黎明航空发动机（集团）有限责任公司，沈阳 110043；2. 山东大学高效洁净机械制造教育部重点实验室， 济南 250061）

切削用量优化是机械加工领域的经典问题。传统上一种常用的优化方法是以泰勒公式（或刀具耐用度公式）为基础，确定约束条件和优化目标，并据此求取优化切削用量。

实际应用中通常以最高生产率、最低生产成本、最高利润率为优化目标。以其中1种或几种进行加权构造出目标函数。近年来，随着计算技术的发展，一些新的计算方法（如遗传算法、粒子群算法等）开始应用到切削用量优化计算中，但是其所依据的基本原则和方法并没有明显变化。一些新的优化模型仍然是在此基础上进一步研究形成的[1-4]。

该切削用量优化计算方法的建立和使用已有多年的历史并在生产中得到广泛应用。在使用普通机床进行一般材料加工、手工刃磨刀具的情况下，其符合性良好。但是在自动化程度较高以及大量使用难加工材料领域（如作者所从事的航空产品生产领域），上述优化方法时常出现一些问题。

另一种重要的优化方法是以马卡洛夫的最优切削温度守恒定律为基础[5]。鉴于两种优化方法在数学模型和理论基础上的差距，使用者在实际工程应用中很少考虑两种理论兼容的可能性，往往做出非此即彼的选择。尽管研究显示，对于难加工材料的切削过程，马卡洛夫的优化模型与实际情形更为接近。但是由于其试验设计更为复杂，同时生产实践中大多不具备相应的切削温度监测条件，故生产企业多数还是以前一种方法进行优化设计。

不过大量研究表明，泰勒公式仅在一个相对窄的范围内近似有效，在更广的范围内具有很大的局限性[5-6]。与常规加工相比，使用自动化设备加工难加工材料时，针对不同优化目标所得出的切削用量分布范围更广，常常超出泰勒公式或刀具耐用度公式的常规应用范围，进而与实际状态产生不同程度的偏离。马卡洛夫的优化模型在一定范围之外也同样存在局限性。而这些在实际的工程应用中又容易被忽略，常常导致意外的经营损失[7]。

因此，对于切削用量可优化区间加以限定是很有必要的。本文中作者提出采用磨损指数确定切削用量优化区间的方法，并对两种优化模型的适用范围加以界定。使用此种方法不需要复杂的试验设备和条件，易于在工程应用中实现。

1 刀具磨损的变化趋势

1.1 泰勒公式及相关经验公式

泰勒公式描述在一定切削条件下刀具耐用度Td与切削速度v之间的关系，可以表述如下：

综合考虑切削深度ap、每转进给量f的变化可以得到广义的刀具耐用度公式：

（1）、（2）式中，Cv、C、Ev、Ea、Ef均为常数，但在难加工材料生产性切削试验中，刀具耐用度Td往往难以准确测定和评价。故常常以检测刀具后刀面磨损宽度VB来取得刀具磨损公式：

式中，t为切削时间，Ct、Et、Eat、Eft、Evt均为常数。该公式成立的条件是试验中刀具均需处于正常磨损阶段[6]。

取VB等于刀具的磨钝标准，t=Td则可以从（3）式推导出相应切削条件下的广义刀具耐用度公式（2）。

1.2 刀具磨损随切削速度的变化

当ap、f、t固定，（3）式形式变为：

对于航空难加工材料，在其常用切削速度范围内，Evt的值通常在2～4之间。

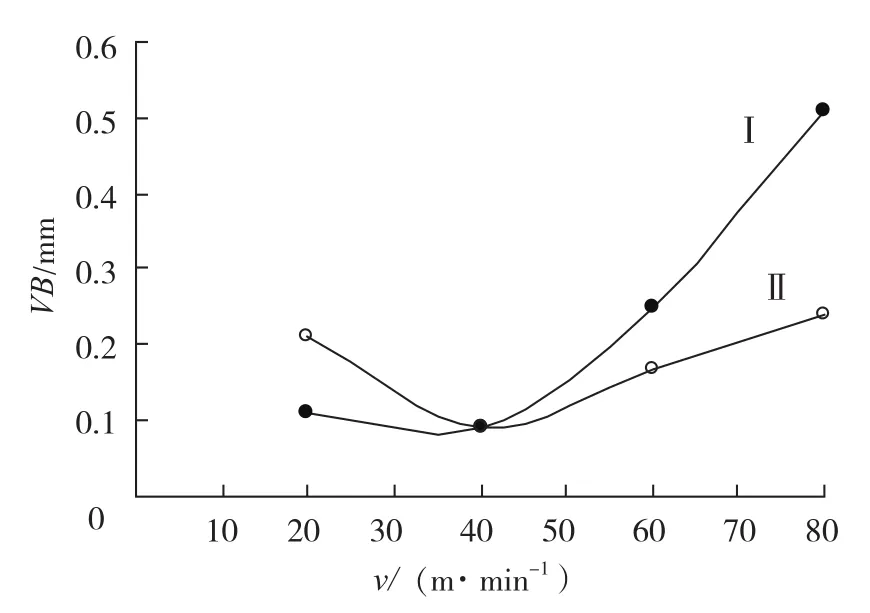
图1 某切削试验VB-v曲线Fig.1 VB-v curve of cutting test

图1显示某次使用涂层硬质合金加工镍基高温合金时的VB-v曲线。图中I为等切削时间曲线，II为等切削路程（等切除量）曲线。

该试验中，VB随v的变化并非如（4）式所表达的呈单调变化趋势，而是在试验范围内存在一最低值。且在等切削时间和等切削路程试验中，最低磨损值所对应的切削速度有所不同。多数针对难加工材料的刀具耐用度试验数据均显现了这样一种趋势[5-7]。

马卡洛夫的切削优化模型可以对此作出较好的解释。按照最优切削温度守恒定律[5]，对于给定的刀具及工件，不同切削用量搭配下的最优切削速度，对应着一个恒定的最优切削温度。图1中曲线II的最低点正对应该种切削用量组合下的最优切削速度。

1.3 刀具磨损随其他切削用量的变化

在一些难加工材料刀具磨损-进给量切削试验中，可以观察到VB-f曲线呈现与VB-v曲线相似的形态（图2中的I、II分别为等切削时间曲线和等切除量曲线），即存在VB最低点。

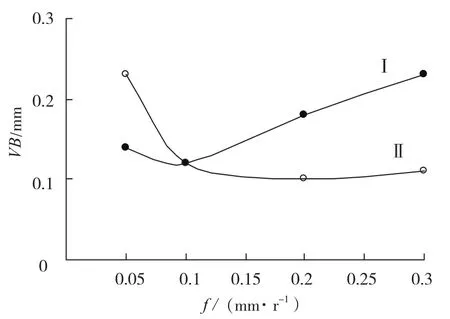
图2 某切削试验VB-f曲线Fig.2 VB-f curve of cutting test

按照马卡洛夫的切削优化理论，在一定切削条件下最优切削速度vo与进给量之间存在如下关系：

式中，Cm、Efv为常数。

通过相关验证试验[8]数据分析可知，在马卡洛夫的优化模型中，VB-f曲线的最低点是可以存在的。它和VB-v曲线最低点同为最优切削速度曲线上某点在两个坐标方向上的投影。在较高切削速度下，这一最低点对应很小的进给量。

但试验显示，在较高切削速度下，如图2所示，VB最低点对应进给量高于该优化模型的理论值很多，出现在远离最优切削速度曲线的位置。经分析可能出于以下原因：由于难加工材料切削硬化层的普遍存在，当进给量小于切削硬化层厚度时，往往发生进给量减小而刀具磨损加剧的情况。同时，刀具的前刀面通常具有特定的槽形，适用于一定的进给量范围。超出此范围则会加剧刀具的磨损。这种情形既不符合广义刀具耐用度公式所表达的趋势，也不符合马卡洛夫的切削优化模型。

难加工材料刀具磨损-切削深度试验中，等切削时间曲线一般呈缓慢平稳上升的趋势，如图3曲线I所示。虽然也存在切削硬化层的影响，但影响较小。

不过对于等切除量试验（保持t×ap恒定，曲线II），在某些试验中会观察到VB随ap的缓慢下降，在切深足够大的情况下，也可发现VB的极小值。

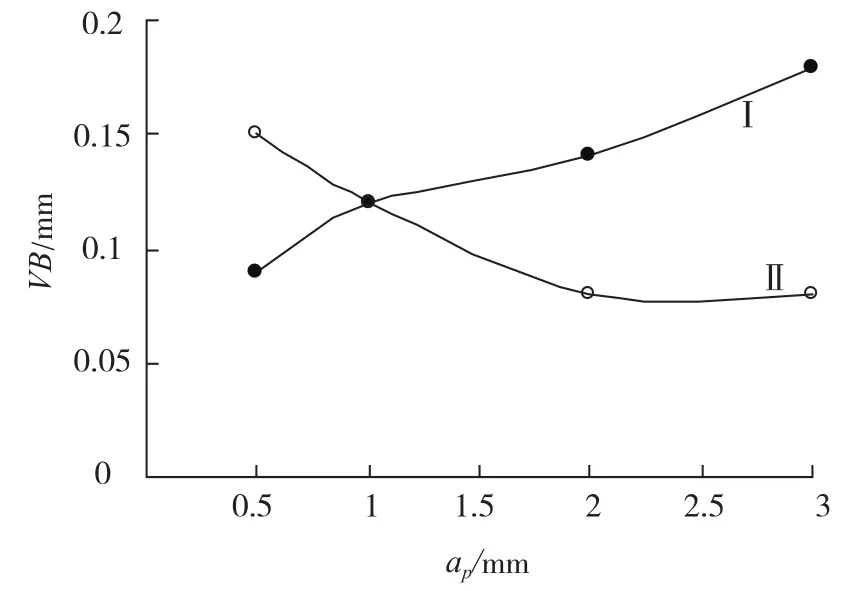
图3 某切削试验VB-ap曲线Fig.3 VB-ap curve of cutting test

2 切削用量可优化区间确定

2.1 磨损指数

综上所述，与广义的刀具耐用度公式所表达的趋势不同，在一定条件下的等切削量切削试验中，存在刀具磨损值最小的切削用量。研究还表明，在同一试验条件下，选取不同的切削用量范围进行切削试验，得出的经验公式中切削用量指数也不尽相同，有随切削用量增长的趋势[9]。如果在较大切削用量范围内考察这一指数，则其并不是一个恒量，而是关于切削用量的函数变量。

将这一变量定义为磨损指数。在等切削量试验中，如果取得一系列VB相对于切削用量P的变化数据（Pn，VBn），则可按下式计算对应于Pn的磨损指数En：

图4为某等切除量切削试验Ev-v曲线。图中曲线Ev值为0的点对应最优切削速度。

2.2 可优化区间边界条件

从工程应用上来讲，磨损指数E＜0的切削用量区间呈现随效率降低刀具磨损反而增加的趋势，显然应当排除在可优化区间之外。在E＞0的区间，在多数切削试验过程之中，可以找到一个E值相对恒定的区域。在此区域内，广义刀具耐用度公式及相关优化方法是适用的。

图4 某等切除量切削试验Ev-v 曲线Fig. 4 Ev-v curve of equal removal rate experiment

随着切削用量的进一步提升，刀具磨损将迅速加剧。可以设定一个Emax值，作为可优化区间的右边界条件。具体设定可根据大多数试验中取得泰勒公式切削用量的指数值范围及对于刀具成本随效率提升不断加剧的可接受程度。一般可将Emax=1作为切削深度ap、进给量f的右边界条件，将Emax=2作为切削速度v的右边界条件。

2.3 特别情形的处理

由于刀具磨损试验结果本身存在较大误差，而磨损指数的计算又会放大这种误差，当数据离散程度较大，则需要根据多次试验数据来进行优选。同时由于刀具磨损规律的复杂性，图4所示的磨损指数形态不是在各类切削试验中所必然观测到的。如果未观测到E小于0或大于Emax的区域，则可以将试验所用的切削用量范围认定为可优化区域。

在轻切削条件下的切削深度试验中，可能存在可用切削深度范围内，Eap始终小于0的情况。使用小直径铣刀加工钛合金时，也可能在其推荐进给量范围内，Ef始终小于0。此种情况下，可以认为不存在该切削用量可优化区间，而将最大切削用量直接判断为最优切削用量。

3 多项切削用量可优化区域

研究表明，切削试验中各因素之间不是相互独立的。由一种切削用量改变而导致切削系统整体变化，通常会导致其他切削用量的磨损指数也随之改变[6]。因而，切削用量的可优化区间也会随着另一种切削用量的变化而变化。

由此可见，在多项切削用量变化的条件下，其可优化区域应是不规则的空间区域。图5示意难加工材料v-f两项切削用量的可优化区间变化范围。其下边界应为马卡洛夫最优切削速度曲线（曲线A，Ev=0），同时也是最佳切削温度的等温线。

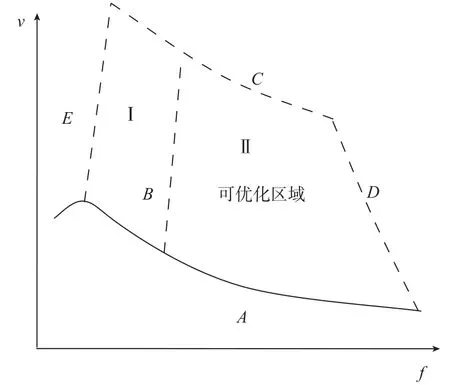
图5 可优化区域Fig.5 Intervals can be optimized

由于加工硬化层的存在，当进给量小于加工硬化层深度，随着切削温度升高和刀具磨损增大，最优切削速度将不会无限上升，而不可避免地会发生逆转。在等切削时间试验条件下，将出现一条取得VB最小值的曲线（曲线E）。该曲线的趋势应与硬化层深度分布一致。一些试验数据表明，最小硬化层深度出现在最优切削速度条件下[6-11]，但另外一些试验数据不支持这一结论。

在等切除量条件下，Ef=0的曲线（曲线B）在曲线E右方，形成可优化区域的左边界。Ev=Evmax（曲线C）、Ef=Efmax（曲线D）形成其他两条边界。目前还缺少足够的试验数据确定曲线B、C、D、E的走势和形态。

对于图中I、II区域，广义刀具耐用度公式和最优切削速度公式都是适用的。但是对于进给量的优化，只有II区域是有意义的。如果因为约束条件的限制只能在I区域内进行优化，则因Ef＜0，进给量取最大值即可。

4 结论

本文对刀具磨损随切削速度以及其他切削用量的变化趋势进行了分析,揭示传统切削优化方法的局限性，并提出一种易于在工程应用中实现的确定切削用量优化区间的新方法。

综上所述,可以得出以下结论:

（1）以刀具耐用度公式和最优切削速度公式为基础的两种传统切削用量优化方法适用范围是有限的，在可优化区间内有效。

（2）磨损指数可以作为判断可优化区间边界的依据。

（3）在多项切削用量变化的条件下，其可优化区域应是不规则的空间区域。

[1]陈志同，张保国. 面向单元切削过程的切削参数优化模型[J].机械工程学报，2009，45(5)：230-236.

CHEN Zhitong, ZHANG Baoguo. Mathematic model on cutting parameter optimization for unit cutting process[J]. Chinese Journal of Mechanical Engineering, 2009, 45(5)：230-236.

[2]冯锦春. 基于遗传算法的切削用量优化研究与实现[J]. 机械设计与制造，2009(7)：226-228.

FENG Jinchun. The research and realization of cutting parameters optimization based on genetic algorithm[J]. Machinery Design &Manufacture, 2009 (7)：226-228.

[3]黄宗南，何岚岚，舒洲. 切削用量遗传优化中的约束条件处理 [J]. 机械设计与研究，2008，24(4)：93-97.

HUANG Zongnan, HE Lanlan, SHU Zhou. Constraints handling in cutting optimization by genetic a lgorithms[J]. M achine Design and Research, 2008, 24(4)：93-97.

[4]张青，陈志同，张平，等. 基于粒子群算法的切削参数优化及其约束处理 [J]. 航空精密制造技术，2010，46(1)：32-36，45.

ZHANG Qing, CHEN Zhitong, ZHANG Ping, et al. An algorithm for cutting parameter optimization and constraint handling based on particle swarm optimization[J]. Aviation Precision Manufacturing Technology, 2010,46(1)：32-36，45.

[5]马卡洛夫. 切削过程最优化[M].杨锦华，袁宁生，王存政，等译. 北京：国防工业出版社，1988.

MAKAROF. Optimization of cutting process[M].YANG Jinhua, YUAN Ningsheng, WANG Cunzheng, et al translated. Beijing：National Defence Industry Press, 1988.

[6]杨荣福，董申. 金属切削原理[M]. 北京：机械工业出版社，1988.

YANG Rongfu, DONG Shen. The principle of metal cutting[M].Beijing：Mechanical Industry Press，1988.

[7]叶洪涛,庞继有.传统切削用量优化方法在现代加工中的局限[J].工具技术,2015,49(3):36-38.

YE Hongtao, PANG Jiyou.Limitation of traditional cutting parameter optimization in modern machining[J].Tool Engineering,2015,49(3):36-38.

[8]盛精，黄丛林，刘超，等. 基于刀具磨损的车削参数优化实验[J]. 机械设计与研究，2013，29(4)：26-80，85.

SHENG Jing, HUANG Conglin, LIU Chao, et al. Experiment and research of optimizing turning parameters based on tool wear[J]. Machine Design and Research, 2013, 29(4)：26-80, 85.

[9]YE Hongtao, WAN Yi, REN Xiaoping, et al. Validity analysis of generalized taylor regression formula by tool wear test for difficult-tomachine materials[J]. Key Engineering Materials, 2014, 589-590: 342-350.

[10]袁哲俊. 金属切削实验技术[M]. 北京：机械工业出版社，1988.

YUAN Zhejun. The experimental technique of metal cutting[M].Beijing：Mechanical Industry Press，1988.

[11]阎光明，杨巧风. 0Cr15Ni7Mo2Al不锈钢铣削加工硬化研究 [J]. 石油矿场机械，2008，37(12)：60-62.

YAN Guangming, YANG Qiaofeng. Study on milling and work hardening of 0Cr15Ni7Mo2Al stainless Steel[J]. Oil Field Equipment, 2008,37(12)：60- 62.