Constructing Invariant Tori for the Spatial Hill Lunar Problem

Dongfeng YAN

1 Introduction and Main Results

The Hill lunar problem deals with the motions of two small masses under the mutual interactions perturbed by a massive body,and it covers some interesting astrodynamical systems,which include a satellite orbiting the planet and perturbed by the Sun.Stemming from the circular restricted three-body problem,Hill’s approximation is achieved by translating the origin of the rotating reference frame to the planet and the unit of the length is scaled byl13,wherelis the mass parameter of the circular restricted three-body problem.For the planar circular Hill lunar problem,[5,10]showed its rich dynamics by computing Poincaré surfaces of the section.In[9],Hénon discovered the main families of periodic orbits and computed the width of the stability regions.For the planar elliptic Hill lunar case,[18]established its dynamics about the periodic solutions and stability regions.

Similar Hill’s approximation can be applied to the spatial Hill lunar problem(see[11]for reference).In[17],Villac derived the following normalized equation for the spatial Hill lunar problem by selecting proper length and time scales:

Our purpose in this paper is to investigate the existence of invariant tori for the spatial Hill lunar problem.We rewrite the above spatial Hill lunar equation as a Hamiltonian system,and then its Hamiltonian takes the form

and the corresponding 2-form is

It is natural to note that this Hamiltonian has two collinear equilibrium points along thex-axis,and we can obtain three pairs of eigenvalues of the linearized equation around the equilibrium solutions,which read

Thus we can put the quadratic term into the normal form

By the Birkhoffnormal form lemma(see[3]),we can put this Hamiltonian into the partial Birkhoff normal form(that is,(2.5)),and then by making use of Moser’s theorem(see[14,Theorem 5.2]),we can derive the hyperbolic invariant tori for the spatial Hill lunar problem.Moreover,the above Hamiltonian has 4-dimensional central manifold,and the standard KAM theorem guarantees the reduced Hamiltonian on its central manifold has 2-dimensional elliptic invariant tori,the motions on which are quasi-periodic.Thus our main results in this paper can be summarized as follows.

Theorem 1.1For the spatial Hill lunar problem(1.4),there are hyperbolic invariant tori in the neighbourhood of the equilibrium,and the corresponding reduced Hamiltonian on the center manifold around the equilibrium has2-dimensional elliptic invariant tori with quasi-periodic solutions along them.

Let us make some comparisons with earlier papers.Villac[17]had never considered the reduced Hamiltonian on the central manifold,while Gómez,Marcote and Mondelo[7]proceeded with the analysis of the dynamics in the central manifold in a semi-analytical way,and provided accurate numerical procedures to compute homoclinic and heteroclinic orbits.However,in our work,we manage to check the non-degenerate condition of the standard KAM theorem analytically,and establish the existence of invariant tori in a neighbourhood of the collinear equilibrium points for the spatial Hill lunar problem.

The following paper is organized as follows.In Section 2,we derive the normal form for the spatial Hill lunar problem.In Section 3,we present the proof the our main theorem with the aid of the KAM theorem.

2 Normal Forms

In order to apply the KAM theorem to the spatial Hill lunar problem,we will derive the normal form of its Hamiltonian at the equilibrium points in this section.

2.1 The normal form for the quadratic term

Consider the spatial Hill lunar problem(1.4),and it is not hard to derive its equilibrium points

From now on we only takeL1into consideration for convenience.After expandingHinto Taylor series atL1,we have

whereCis a dynamically irrelated constant,and we omit the terms with order higher than 4.Consider the quadratic term

where

and the corresponding Hamiltonian matrix takes

After simple computations,we derive the eigenvalues ofA

andcorrespond to eigenvectors:

By making use of discussions about the canonical forms for Hamiltonian matrices in[12,19],we seek a real symplectic matrixTto putAinto the canonical form,such that

Denoteand sincewe have

where

From the factT−1AT=BandAT=TB,we have

DenoteThen we have

and thus

We can constructsimilarly,soTtakes the following form:

So we can derive the normal form for the quadratic part ofH,

where

Next,we introduce a symplectic transformation

where

ThenQtakes the form

2.2 The partial Birkhoffnormal form

To derive the partial Birkhoffnormal form,we introduce the symplectic coordinates

Then

Under these variables,we have

It is not difficult to note the fact that there are no integerssatisfying

such that

So by the Birkhoff normal form lemma(see[3]),we can putHinto the partial Birkhoff normal form.As a result,we can find HamiltonianwhereWidenotes the homogeneous polynomial of orderi+2 aboutsuch thatis in the partial Birkhoffnormal form,wheredenotes the time-1 map of Hamiltonian vector fieldXW.

To proceed,we introduce some notations.Denote

wheredenotes the homogeneous polynomial of orderi+2.Then we have

From

we have

Assume

Then

Thus we can solve the above equation and get

Meanwhile,(2.3)turns into

and then by the Birkhoffnormal form lemma(see[3]),we can deriveW2similarly such that there are only homogeneous monomials aboutin.Thus we have

where

andα,β,γare real numbers.

Hence,the partial Birkhoffnormal form of the spatial Hill lunar problem is

whereα,β,γ,a11,a12,a22are real numbers.

3 Proof of Theorem 1.1

To prove the first part of our main theorem,we investigate the Hamiltonianin the neighbourhood of the equilibrium pointL1,where

TreatH+as a perturbation ofH0,for the non-perturbed HamiltonianH0,which has 2-dimensional invariant tori

The Moser’s theorem(see[14,Theorem 5.2])ensures the preservation of those invariant tori with a slight deformation for the perturbedHnew.Next we need to check the conditions of Moser’s theorem:

(1)Hnewis 2πperiodic inϕi,i=1,2,and

(2)(The non-degenerate condition)Ifp3=q3=0,then

(3)Whenp3=q3=0,I=(I1,I2)belongs to some open set in R2,

is a diagonal matrix with real entries,so it does not have any pure imagine eigenvalue.

Hence all the conditions in Moser’s theorem are ful filled,which makes sure that the Moser’s theorem can be applied.To proceed with the proof of the second part in the main theorem,we need the following KAM theorem.

Lemma 3.1(see[2])Consider a Hamiltonian system with n degrees of freedom in a neighbourhood of an equilibrium point located at the origin,and ω1,···,ωnare its eigenfrequencies.Suppose that the Hamiltonian function has the following Birkhoffnormal form:

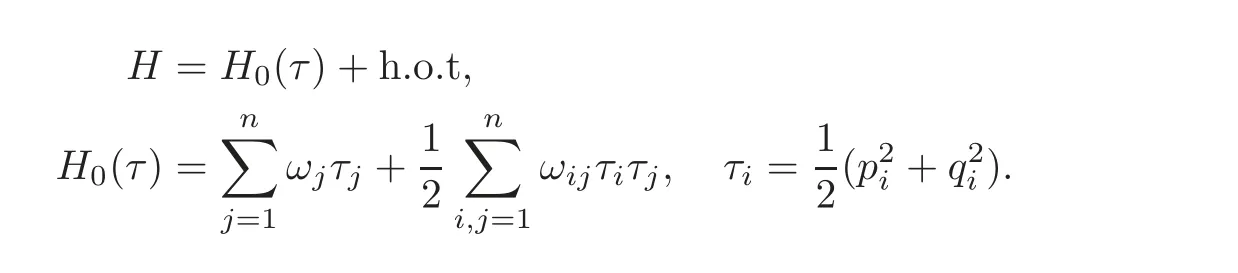
Then,

(i)if the system ful fills the non-degenerate condition

then,the Hamiltonian system has invariant tori close to the tori of the linearized system,and these tori form a set whose relative measure tends to1as it tends to the origin.

(ii)if the iso-energetically non-degenerate condition

holds,the Hamiltonian system also has invariant tori,and such tori occupy a larger part of each energy level passing near the equilibrium position.

Remark 3.1For the proof of this KAM theorem,see[1,15].

The first step is to study the spatial Hill lunar problem on its central manifold.Under the symplectic variables(I1,I2,ϕ1,ϕ2,p3,q3),the Hamiltonian for the spatial Hill lunar problem takes the form

where

andH+(I1,I2,ϕ1,ϕ2,p3,q3)denotes the terms with order higher than 4.

From the discussions about the central manifold in[4,8,13],we know that the spatial Hill lunar problem has the 4-dimensional central manifold atL1,and moreover,a Hamiltonian reduced on its central manifold is still a Hamiltonian.Furthermore,if we takep3=0,andq3=0,we will obtain the reduced Hamiltonian on this central manifold,that is,

where

For the integral partHc0,it has 2-dimensional elliptic invariant tori

In the neighbourhood of the equilibrium point,we can treatHc1(I1,I2,ϕ1,ϕ2)as a small perturbation ofHc0(I1,I2),and the above standard KAM theorem guarantees the preservation of the elliptic invariant tori Π.

The second step is to check the non-degenerate conditions:

(1)(the non-degenerate condition)

(2)(the iso-energetically non-degenerate condition)

SinceD2continously depends onI1,I2,we only need to check the condition at the equilibrium

Thus Lemma 3.1 holds true,which guarantees the existence of 2-dimensional elliptic invariant tori for the reduced Hamiltonian of the spatial Hill lunar problem on its central manifold.Moreover,along these tori,the motions are quasi-periodic

Finally,we finish the proof of Theorem 1.1.

AcknowledgementThe author is very grateful to the referees for their invaluable suggestions.

[1]Arnold,V.I.,Small denominators and problems of stability of motion in classical and celestial mechanics,Usp.Mat.Nauk.,18(6),1963,91–192;Engl.Transl.,Russ.Math.Surv.,18(6),1963,85–191.

[2]Arnold,V.I.,Kozlov,V.V.and Neishtadt,A.I.,Mathematical Aspects of Classical and Celestial Mechanics,3rd ed.,Springer-Verlag,Berlin,2006.

[3]Birkhoff,G.D.,Dynamical Systems,Amer.Math.Soc.,Providence,RI,1927.

[4]Carr,J.,Applications of Center Manifold Theory,Springer-Verlag,Berlin,1981.

[5]Chauvineau,B.and Mignard,F.,ATLAS of the Circular Planar Hills Problem,Observatoire de la Cote dAzur,CERGA,1991,1–71.

[6]Delshams,A.,Masdemont,J.and Roldán,P.,Computing the scattering map in the spatial Hill’s problem,Discrete Contin.Dyn.Syst.Ser.B,10(2–3),2008,455–483.

[7]Gómez,G.,Marcote,M.and Mondelo,J.M.,The invariant manifold structure of the spatial Hill’s problem,Dyn.Syst.,20,2005,115–147.

[8]Guckenheimer,J.and Holmes,P.,Nonlinear Oscillations,Dynamical Systems,and Bifurcations of Vector Fields,Springer-Verlag,New York,1991.

[9]Hénon,M.,Numerical exploration of the restricted problem,V,Hills case:Periodic orbits and their stability,Astronomy and Astrophysics,1,1969,223–238.

[10]Hénon,M.,Numerical exploration of the restricted problem,VI,Hills case:Non-periodic orbits,Astronomy and Astrophysics,9,1970,24–36.

[11]Hénon,M.,Vertical stability of periodic orbits in the restricted problem,Hills case,Astronomy and Astrophysics,30,1974,317–321.

[12]Laub,A.and Meyer,K.R.,Canonical forms for symplectic and Hamiltonian matrices,Celest.Mech.,9,1974,213–238.

[13]Mielke,A.,Hamiltonian and Lagrangian Flows on Center Manifolds with Applications to Elliptic Variational Problems,Springer-Verlag,Berlin,1991.

[14]Moser,J.,Stable and Random Motions in Dynamical Systems with Special Emphasis on Celestial Mechanics,Princeton University Press,Princeton,2001.

[15]Moser,J.,Lectures on Hamiltonian Systems,Mem.Amer.Math.Soc.,81,American Mathematical Society,Providence,RI,1968.

[16]Vashkovyak,M.A.and Teslenko,N.M.,On periodically evolving orbits in the single averaged Hill problem,Astronomy Letters,34,2008,280–288.

[17]Villac,B.F.,Dynamics in the Hill problem with applications to spacecraft maneuvers,Ph.D.Dissertation,University of Michigan,Ann Arbor,Michigan,2003.

[18]Voyatzis,G.,Gkolias,I.and Varvoglis,H.,The dynamics of the elliptic Hill problem:Periodic orbits and stability regions,Celestial Mechanics and Dynamical Astronomy,113(1),2012,125–139.

[19]Wintner,A.,The Analytic Foundations of Celestial Mechanics,Princeton University Press,Princeton,1941.