A Note on Model(Co)slice Categories∗
Zhiwei LI
1 Introduction
Given a categoryCand a morphisminC,one can construct adjunctions between coslice categoriesandand between slice categoriesandIfCis a closed model category,all these(co)slice categories inherit a model structure fromC.In this case,the adjunctions between these(co)slice categories are Quillen adjunctions.Meanwhile,if we start from a Quillen adjunction between two closed model categoriesCandD,we can also construct Quillen adjunctions between some(co)slice categories.This note is aimed to characterize when these adjunctions are Quillen equivalences.
As an application of these characterizations,we construct a triangle equivalence between the stable category of a weakly idempotent complete Frobenius category and the homotopy category of its coslice category(see Corollary 3.3).As a byproduct,we get a non-pointed model category whose homotopy category is a triangulated category(see Theorem 3.1).This shows that the pointed condition of Quillen’s theorem(see[8,Chapter I,Section 2,Theorem 2])is not always necessary.
The contents of the note are as follows.In Subsection 2.1,we recall the standard material of Quillen equivalences.In Subsections 2.2–2.3,we recall the notion of model(co)slice categories and construct six Quillen adjunctions between model(co)slice categories(see Proposition 2.2).In Section 3,we give a proposition to distinguish when these Quillen adjunctions are Quillen equivalences(see Proposition 3.1).We end up this note by proving Theorem 3.1.
2 Preliminaries of(Co)slice Categories and Quillen Equivalences
In this section we recall the notions of Quillen equivalences and model(co)slice categories.Our main references about model categories are[8,1,5,4].
2.1 Quillen equivalences
Recall that a categoryCis said to be bicomplete if it contains small limits and colimits.A closed model categoryCis a bicomplete category in which there are three classes of morphisms,called co fibrations, fibrations and weak equivalences and they satisfy some axioms.We will denote the three classes of morphisms by Cof(C),Fib(C)and We(C),respectively.A morphism which is both a(co) fibration and a weak equivalence is called an acyclic(co) fibration.An objectX∈Cis called co fibrant ifand fibrant ifwhereØis the initial object ofCand∗the terminal object ofC.We useCcandCfto denote the classes of co fibrant and fibrant objects,respectively.An object inis called bi fibrant.
Suppose thatCandDare closed model categories.An adjunctionis called a Quillen adjunction ifFpreserves co fibrations and acyclic co fibrations,or equivalently,Gpreserves fibrations and acyclic fibrations(see[5,De finition 1.3.1,Lemma 1.3.4]).Sometimes we will callFa left Quillen functor andGa right Quillen functor.
De finition 2.1(see[5,De finition 1.3.12])A Quillen adjunctionis called a Quillen equivalence if for all X∈Ccand Y∈Df,a morphism if and only if
If(F,G)is a Quillen equivalence,then the left derived functor LFand the right derived functor RGexist(see[8,Chapter I,Section 4]).Furthermore,they induce an equivalent adjunction(LF,RL):between the homotopy categories(see[8,Chapter I,Theorem 3]).
In a model categoryC,we useto denote the co fibrant approximation of an objectX(it is an acyclic fibration)andthe fibrant approximation ofX(it is an acyclic co fibration),respectively(see[8,Chapter I,Section 1]or[1,Section 5]).The following is the most useful criterion for checking when a given Quillen adjunction is a Quillen equivalence.
Proposition 2.1(see[5,De finition 1.3.13,Corollary 1.3.16])Suppose that(F,G,ϕ;η,ε):is a Quillen adjunction.The following are equivalent:
(i)(F,G,ϕ)is a Quillen equivalence.
(ii)is an adjoint equivalence of categories.


2.2 The model(co)slice categories
De finition 2.2Let C be a category.For an object X in C,the coslice categoryis the category in which an object is a morphism in C,and a morphism from tois a morphism α:in C such that u′=α ◦u.The composition of morphisms is de fined by the composition of morphisms in C.
Dually,we de fine the slice categoryoverX.
Now letCbe a closed model category.If we de fine a morphism inandis a weak equivalence,co fibration,or fibration if it is one inC,then both the coslice categoryand the slice categorybecome closed model categories(see[4,Theorem 7.6.5]).In this case,we calla model coslice category anda model slice category.
Lemma 2.1Let C be a model category.Then

Proof(i)Note that,the initial object in(X↓C)isand the terminal object isFrom these,the statement(i)can be veri fied directly.Dually,we can prove(ii).
2.3 Quillen adjunctions between model(co)slice categories
LetCbe a bicomplete category andbe a morphism inC.There are two adjunctions:
(1)
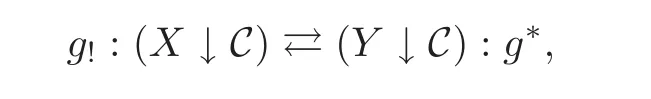
whereg∗takes the objectthe compositionandg!sendsto its cobase change alonggandto the induced morphismby the universal property of pushouts and they fit into the following commutative diagram:

with the three squares being pushouts.The unit of this adjunction isfor anyu∈(X↓C),wheresuis de fined in the above diagram.
(2)

where the constructions of the functorsg∗andare dual to(1).In fact,g∗takes the objectto the compositionand,andtakes the objectYto its base change alonggandto the induced morphismby the universal property of pullbacks and they fit into the following commutative diagram:

with the three squares being pullbacks.The counit of this adjunction isfor anywheretvis de fined in the above diagram.
In particular,if we takeX=Øto be the initial object ofC,theng∗is just the forgetful functor fromtoand if we takeY=∗to be the terminal object ofC,theng∗is just the forgetful functor from
If we already have an adjunctionbetween the bicomplete categoriesCandD,then for any objectX∈CandY∈D,(S,U)induces the following four adjunctions.
(3)

wheresendsandwhilesendsto the compositionandThe unit of this adjunction isfor anyin
(4)

whereSXsendstoandsendsto the base change ofU(v)along the unitηXandto the induced morphism fromby the universal property of pullbacks and they fit into the following commutative diagram:

with the three squares being pullbacks.The counit of this adjunction isfor anywherelvis de fined in the above diagram.
(5)

where the constructions ofandare dual to(3).In fact,sendsto the compositionandwhilesendsvtoU(v)andThe counit of this adjunction isfor anyin
(6)

where the constructions ofandare dual to(4).In fact,sendstoU(v)andsendsto the cobase change ofS(u)along the counitεYandto the induced morphism fromby the universal property of pushouts and they fit into the following commutative diagram:

with the three squares being pushouts.The unit of this adjunction isfor anyin(U(Y)↓C),wheremuis de fined in the above diagram.
We have the following proposition about these adjunctions,in which the first statement in some special case has been discussed in[5,Chapter 1,Section 3]and[7,Chapter 16,Section 2].
Proposition 2.2(i)Let C be a closed model category and g:X→Y be a morphism in C.Then the adjunctions(1)and(2)are Quillen adjunctions.
(ii)Let C and D be two closed model categories.Assume thatis a Quillen adjunction and X∈C,Y∈D.Then the adjunctions(3)–(6)are Quillen adjunctions.Moreover we have

and

where the compsoitions of the adjunctions are in the sense of TheoremIV.8.1of[6].
ProofThese statements can be proved directly.We leave the details to the interested reader.For example,sinceg∗(h)=hfor any morphismin(Y↓C)andhis a fibration or an acyclic fibration in(Y↓C)if and only if it is one inpreserves fibrations and acyclic fibrations.Therefore the adjunction(1)is a Quillen adjunction.
Assume now thatCandDare closed model categories and denote byC∗=(∗↓C)andthe slice categories ofCandDinduced by the terminal object∗,respectively.Ifis a Quillen adjunction,M.Hovey de fined a functorU∗fromby mapping objectin[5].This functor is a right Quillen functor as proved in[5].Note that if we denote the morphismasginD∗,thenU∗is the composition of the functorsSo by Proposition 2.2,this functor has a left adjointS∗=S∗◦g!,and then we get Proposition 1.3.5 of[5]directly.
Corollary 2.1(see[5,Proposition 1.3.5])A Quillen adjunction(S,U)induces a Quillen adjunction
3 Main Results
Proposition 3.1(a)Let C be a closed model category and g:be a morphism in C.Then
(i)the adjunctionis a Quillen equivalence if and only if the cobase change of g along u for each co fibration u:with C∈C is a weak equivalence;
(ii)dually,the adjunctionis a Quillen equivalence if and only if the base change of g along v for each fibration v:with Y∈C is a weak equivalence.
(b)Let C and D be closed model categories andbe a Quillen equivalence.Then given any object X∈C and Y∈D,
(i)if X∈Cc,the adjunctionis a Quillen equivalence;
(ii)if Y∈Df,the adjunctionis a Quillen equivalence;
(iii)if S(X)∈Df,the adjunctionis a Quillen equivalence if and only if the base change of ηXalong v for each fibration v:with D∈D is a weak equivalence;
(iv)if U(Y)∈Cc,the adjunctionis a Quillen equivalence if and only if the cobase change of εYalong u for each co fibration u:SU(Y)→D with D∈D is a weak equivalence.
ProofBy Proposition 2.2,all the adjunctions in the statements are Quillen adjunctions.We only prove the assertions(i)of(a),(i)and(iii)of(b).The others can be proved dually.
The proof of(a)(i).On the one hand,sinceg∗(h)=hfor any morphisminifg∗(h)is a weak equivalence,so ish.On the other hand,for anyin(see Lemma 2.1),the unit of the adjunction(g!,g∗)is(see the construction of this adjunction)which is the cobase change ofgalongu.So by(iv)of Proposition 2.2,(g!,g∗)is a Quillen equivalence if and only if the composite

is a weak equivalence.Sinceis a weak equivalence,by the 2-out-of-3 axiom of weak equivalences,we know that(g!,g∗)is a Quillen equivalence if and only ifsuis a weak equivalence.
The proof of(b)(i).Ifis inthenhis a morphism inDf,andRecall that the unit of the adjunctionisfor any(see the construction of this adjunction).Ifuis insinceX∈Cc,we know thatC∈Cc.Thus by(iv)of Lemma 2.2,(SX,UX)is a Quillen equivalence if and only if whenis a weakly equivalence,so ishand the compositionis a weak equivalence.But again by(iv)of Lemma 2.2,this holds since(S,U)is a Quillen equivalence.
The proof of(b)(iii).By assumption and(ii)of(b),we know thatis a Quillen equivalence.Sinceby(ii)of Proposition 2.2,we know thatis a Quillen equivalence if and only ifis a Quillen equivalence by Corollary 1.3.15 of[5].Then the assertion follows from(ii)of(a).
Corollary 3.1(see[5,Proposition 1.3.7])Suppose that(S,U):is a Quillen equivalence,and suppose in addition that the terminal object∗∈Ccand that S preserves the terminal object.Thenconstructed as in Corollary2.1is a Quillen equivalence.
ProofIn this case,is a Quillen equivalence by Proposition 3.1.
Recall that a closed model categoryCis called left proper if every cobase change of a weak equivalence along a co fibration is a weak equivalence.Dually,Cis called right proper if every base change of a weak equivalence along a fibration is a weak equivalence.By Proposition 3.1,we can redescribe the left or right properness of a model category by Quillen equivalences.
Corollary 3.21This should be the right version of Proposition 16.2.4 of[7],and there the authors claimed that a closed model category C is left proper or right proper if and only if(g!,g∗)or(g∗,g!)is Quillen equivalence for a given morphism g.For a counter example see Remark 3.1.(1)A closed model category C is left proper if and only if(g!,g∗)is a Quillen equivalence for every weak equivalence g:
(2)A closed model category C is right proper if and only if(g∗,g!)is a Quillen equivalence for every weak equivalence g:
Remark 3.1In general,ifgis not a weak equivalence,and evenCis proper,(g!,g∗)is not necessarily a Quillen equivalence.For example,takeC=modk[x]/(x2)wherekis a field.ThenCis a proper model category in which weak equivalences are stable equivalences and every object is bi fibrant,and its homotopy category is the stable categoryTakeg=0:0→k,and thenis the unit of the adjunctionIn this case,every object is fibrant,the morphisms in(iv)of Proposition 2.2 are justηCfor anyC∈C.Butis in no way a weak equivalence.So the Quillen adjunctionis not a Quillen equivalence.
IfFis a weakly idempotent complete Frobenius category,thenFhas a canonical model structure in which the co fibrations are the monomorphisms,the fibrations are the epimorphisms and the weak equivalences are the stable equivalences(see[2,Theorem 3.3]).LetAbe any nonzero projective-injective object inF.Takeand thenis a weak equivalence for anyC∈F.By Proposition 3.1,we have a Quillen equivalence(0!,0∗):So the derived functors of 0!and 0∗are equivalences of the homotopy categories between Ho(F)and HoNote that in this case,the homotopy category Ho(F)is just the stable category(see[3,Chapter I,Section 2.2])which is a triangulated category by Theorem 2.6 of[3].If we can show that the homotopy category Hois a triangulated category,then the derived adjunctionwill be a triangle equivalence since Quillen equivalences are automatically triangle equivalences if the corresponding homotopy categories are triangulated categories(see[8,Chapter I,Theorem 3]).
Next we will show that the homotopy category Hois a triangulated category.And then we give the promised example as advertised in the introduction since the coslice categoryis not pointed by noting that its initial object isand its terminal object is
Theorem 3.1The homotopy categoryHois a triangulated category.
ProofSinceFcf=FandAis injective,we know thatand co fibrant objects in(A↓F)are split monomorphisms inFwith domainA.So for any objectu∈(A↓F)c,we may writeuasup to isomorphism.The morphisms fromtoare of the formBy Quillen’s homotopy category theorem(see[8,Theorem I.1]),we know that the homotopy category Ho(A↓F)can be realized as the quotient categorywhere∼is the homotopy relation.For details,we refer the reader to Section 1 of Chapter I of[8]or Sections 4–5 of[1].
Letbe the subcategory of(A↓F)cconsisting of the objects of the formand morphisms fromhas zero object


whereis an injective preenvelope ofCinF.Given any morphismthere is a morphismsuch thatsinceAis injective.Thenis a cylinder homotopy frominThat isinMeanwhile,it is easy to prove that given any two morphismsinthey are cylinder homotopic if and only if they are cylinder homotopic inSo we haveIn particular,
We can use Quillen’s Theorem I.2 of[8]to the homotopy category.Recall thatis a very good cylinder object ofwhereI(C)is an injective preenvelope ofC.By the construction of the suspension functor of the homotopy category(see[8,The proof of Theorem 2 in Chapter I]),we may de finewhereis the suspension functor of the stable categorywhich is an automorphism of(see[3,Chapter I,Proposition 2.2]).Then it can be veri fied directly that the suspension functor Σ de fined above on the homotopy categoryis an autoequivalence and thusis a triangulated categories by Propositions 5–6 in Section I.3 of[8].
Corollary 3.3The derived functorL0!:is a triangle equivalence with quasi-inverseR0∗.
ProofBy construction,is a Quillen equivalence.Then the derived adjunctionis an equivalent adjunction andis a triangle equivalence by Theorem I.3 of[8].
Remark 3.2Dually,we can construct a slice categoryfor a nonzero projectiveinjective objectA,and there is a triangle equivalence
AcknowledgementsThe author would like to thank Xiao-wu Chen,Guodong Zhou and Xiaojin Zhang for their helpful discussions and encouragements.He would also like to thank the referee for his or her helpful comments and suggestion on the adjunctions(4)and(6).
[1]Dwyer,W.G.and Spalinski,J.,Homotopy Theories and Model Categories,Handbook of Algebraic Topology,James,I.M.(ed.),Elsevier Science B.V.,1995.
[2]Gillespie,J.,Model structures on exact categories,J.Pure Appl.Algebra,215,2011,2892–2902.
[3]Happel,D.,Triangulated Categories in the Representation Theory of Finite-Dimensional Algebras,London Math.Soc.Lecture Note Series,Vol.119,Cambridge University Press,Cambridge,1988.
[4]Hirschhorn,P.S.,Model Categories and Their Localizations,Mathematical Surveys and Monographs,Vol.99,Amer.Math.Soc.,Providence,RI,2003.
[5]Hovey,M.,Model categories,Mathematical Surveys and Monographs,Vol.63.Amer.Math.Soc.,Providence,RI,1999.
[6]Mac lane,S.,Categories for the Working Mathematician,Grad.Texts in Math.,Vol.5,Springer-Verlag,New York,1971.
[7]May,J.P.and Ponto,K.,More concise Algebraic Topology:Localization,Completion,and Model Categories,Chicago Lectures in Math.,University of Chicago Press,Chicago,IL,2012.
[8]Quillen,D.G.,Homotopical Algebra,Lect.Notes in Math.,Vol.43,Springer-Verlag,Berlin,1967.
 Chinese Annals of Mathematics,Series B2016年1期
Chinese Annals of Mathematics,Series B2016年1期
- Chinese Annals of Mathematics,Series B的其它文章
- Existence and Global Asymptotic Behavior of Positive Solutions for Sublinear and Superlinear Fractional Boundary Value Problems∗
- Null Controllability of Some Reaction-Diffusion Systems with Only One Control Force in Moving Domains∗
- Degenerate Nonlinear Elliptic Equations Lacking in Compactness
- Continuous-Time Independent Edge-Markovian Random Graph Process∗
- Eventual Positivity of Hermitian Polynomials and Integral Operators
- Characterization of Groups L2(q)by NSE Where q∈ {17,27,29}∗
