Null Controllability of Some Reaction-Diffusion Systems with Only One Control Force in Moving Domains∗
J.M.CLARKA.MARINHO S.B.de MENEZESA.T.LOUREDO
1 Introduction and Main Results
In this article we investigate the question of local null controllability of a semilinear coupled parabolic system in the case of time dependent domains with a single control force.To make notations clear,let Ω be a bounded connected open set of Rnwith the boundaryC2.ForT>0,we represent byQTthe cylinder Ω×(0,T)of Rn+1with a lateral boundaryde fined by Γ×(0,T).Let us consider a family of functionswhere for eacht,τtis a deformation of Ω into an open bounded set Ωtof Rnde fined by

Fort=0,we identify Ω0with Ω andτ0with the identity mapping.For convenience of notation,for vectory∈Ω,we will writey=(y1,y2,···,yn)and the points in the deformed domain Ωt,0<t<T,will be denoted byx=(x1,x2,···,xn).The smooth boundary of Ωtis represented by Γt.The non-cylindrical domainand its lateral boundaryare de fined by

respectively.
We assume the following regularity on the functionsτtfor 0≤t≤T:
(A1)τtis aC2diffeomorphism from Ω to Ωt.
(A2)τtlies in
Thus we have a natural diffeomorphismde fined by

To simplify the presentation,the reference domain Ω is assumed to be bounded and of classC2.Nevertheless,we remark that most of the results we present here still hold when Ω is Lipschitz continuous and unbounded.The regularity assumptions on the diffeomorphismτtmay also be weakened.However,the minimal assumptions on the reference domain Ω and the transformationτtwill depend very much on the notion of solution and the type of control problem under consideration.
Concerning the class of domainswhich we are considering,it is important to point out that the assumptions above are not very restrictive.For instance,the condition(A2)thatτtdepends in aC1way on time(that,in practice,can often be replaced by a Lipschitz dependence)indicates that the domain does not evolve in time too roughly but allows all kinds of deformations on its shape.But,the conditions that Ωtcan be mapped into the reference domain Ω at everytby means of aC2diffeomorphism impose that the topology of Ωtdoes not change as time evolves.This is the main restriction that we impose on the geometry of the space-time domainunder consideration.In particular,we do not address here the problems in which holes appear or disappear in Ωtas time increases.This type of situation requires a separate analysis since solutions may develop singularities at those points where the topology of Ωtchanges.
Our main goal is to establish the null controllability for the following general reactiondiffusion system which arises in mathematical biology:

where the control forceacts on a unique equation of the system through an arbitrarily small open setwhereis the image byτtof a non-empty open subsetωof Ω.
In(1.1)we haveis the characteristic function ofandandare the initial states.
Throughout this paper we assume that the nonlinear functionsare globally Lipschitz andfi(0,0)=0.By this,we mean that there existsuch that
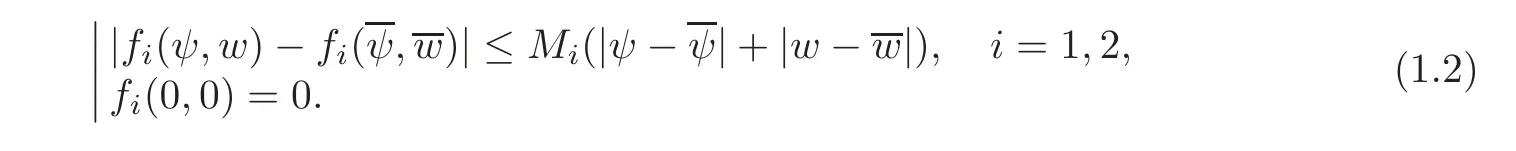
Assume also that there exists a positive constantC0>0 such that

Under natural hypotheses on thewe see that for eachthere exists exactly one solution(1.1),with

The main aim of this paper is to analyze the controllability properties of(1.1)when the control acts on a single equation of system.
The system(1.1)is to be said null controllable at timeTif the following holds:For any giventhere exist controlssuch that the corresponding solutions to(1.1)satisfy

with an estimate of the form

The system(1.1)is to be said locally null controllable at timeTif the previous property holds for anyin a ballB(0;δ)⊂L2(Ω),withδdepending onT.
Recently,important progress has been made in the controllability analysis of semilinear parabolic equations.We refer to the works[7–8,10–11,14]and the references therein in the context of bounded domains,and the works[3,6]in the context of more general domains.It is natural,from both the theoretical and applied viewpoints,to try to extend the known results to systems of kind(1.1).It is particulary important to highlight that system(1.1)has only one control,which is in accordance with the theoretical philosophy of trying to control a system with the least possible controls;to this direction we cite[1,12,16–17].
Our main result is the following.
Theorem 1.1Assume that the non-cylindrical domainand functions fi,i=1,2,satisfy the geometric conditions(A1)–(A2)and the conditions(1.2)–(1.3)respectively.Then the nonlinear system(1.1)is locally null controllable at any time T>0.
The methodology in the present paper consists in turning the non-cylindrical state equation(1.1)into a cylindrical one(see(1.8)below)by the diffeomorphismτt.
To carry on this methodology,we first denote byϕt(x)the inverse map ofτt,that is,According to the assumption(A1),ϕtis aC2-map from Ωtto Ω,for all 0≤t≤T.We shall use the notationϕ(x,t)=ϕt(x).Thus the state onQTis de fined by

Equivalently inwe have

Therefore,the initial-boundary value problem(1.1)is equivalent to:

where

The system(1.8)is a variable coefficient parabolic equation in the cylindrical domainQT.From the technical point of view,a new problem arises because the state equation(1.8)contains a uniformly coercive operatorMore precisely,forand by Gaussian lemma,we obtain the bilinear formα(t,ψ,w)de fined by



proving the coercivity ofαinNote that according to assumptions(A1)and(A2),the boundary value problem(1.8)is a classical problem studied by Lions in[18].If we takeandthen(1.8)has a strong solutionψ,w∈Otherwise,ifψ0,w0∈L2(Ω)andg∈L2(0,T;L2(Ω)),then(1.8)has a weak solutionIn both cases we have uniqueness.
By using the diffeomorphismfrom,we obtain a unique solutionto the problem(1.1)with the regularity,namely:
(1)Ifthen
(2)Ifthen
At this point we underline that,under assumptions(A1)–(A2),the transformationdoes indeed map the space of functionsinto
For a detailed discussion about the existence,uniqueness and regularity of solutions to the system(1.1),we refer to[23].There,they have used the energy method combined with Poincaré’s inequality(satis fied uniformly in the domains Ωtfor all 0≤t≤T),the uniform(with respect tot)elliptic regularity,and the classical trace results and interpolation.They did not use the diffeomorphismfromQTtoand they worked directly on the system(1.1)to see how the structure of the non-cylindrical domain affects the estimates that are used in the energy method.
This paper is organized as follows.Section 2 is devoted to proving the null controllability of a linearized system,which is similar to(1.8).In Section 3,we prove Theorem 1.1 by a fixed point method.
We close this section by mentioning some basic references on the analysis of partial differential equations in non-cylindrical domains.Among many references we mention the following:Lions[19],Cooper and Bardos[5],Medeiros[20],Inoue[15],Nakao and Narazaki[23]for wave equations;Bernardi,Bonfanti and Lutteroti[2],Miranda and Medeiros[22]for Schrödinger equations;He and Hsiano[13]for Euler equations;Miranda and Limaco[21]for Navier-Stokes equations;Chen and Frid[4]for hyperbolic systems of the conservation law.
2 Analysis of the Controllability of the Linearized System
The main result of this article will be proved in Section 3 by means of a fixed point argument.For this,we observe that for anyψ,w∈L2(QT),the following identity holds:

whereanddenote the partial derivatives off1with respect to the variablesψandw,respectively,and the functionsa(ψ,w)andb(ψ,w)are de fined as

Similarly,we de fine the functionsc=c(ψ,w)andd=d(ψ,w)as

Note that

Moreover,we assume the bounds:

whereM1,M2are the positive constants given in(1.2).
With this notation,the system(1.8)can be rewritten in the form

Givenwe now consider the linearized system

Observe that the system(2.7)is linear on the statesψandw,and has potentialsa,b,c,d∈L∞(QT)satisfying the uniform bound given in(2.5).
Again,with this notation we rewrite the system(2.7)as

As usual,the controllability of(2.8)is closely related to the properties of the solutions to the associated adjoint states.In this case,the adjoint systems are

whereA∗(t)is the formal adjoint of the operatorA(t),uT,vT∈L2(Ω).
Next we sketch the points used in the proof of the null controllability of the system(2.8)using the observability estimate.First,we use a global-Carleman inequality satis fied by the solutions to(2.9).Second,this inequality allows us to establish an observability estimate.Third,we prove the null controllability of(2.8)by using the observability estimate.
In this approach,the following technical result,due to Fursikov and Imanuvilov[11],is fundamental.
Lemma 2.1Letbe a non-empty open set.There exists a functionsatisfying

Let us introduce the functions

wherefor 0≤t≤Tandλ>0.
We will use the following Carleman inequality.
Theorem 2.1There exist positive constants λ0,s0,C0and C1such that,for any s≥s0,any λ≥λ0and any solution to(2.9)(corresponding to some uT,vT∈L2(Ω)),one has

Furthermore,C0,C1and λ0depend only onΩand ω,and s0can be chosen of the form

This result was essentially proved in[11](in fact,similar Carleman inequalities were established there for much more general linear parabolic equations);see also[9].In fact,the coefficients of the principal partA∗(t),according to the assumptions(A1)and(A2),are of classC1anda,b,canddare uniformly bounded.Under these conditions,the Carleman inequalities presented in[11]or[9]guarantee(2.11)and(2.12).
We remark that the explicit dependence on time of the constants is not given in[11].We refer to[9]where the above formula fors0was obtained.
Remark 2.1The Carleman inequalities presented in[11]and[9]were used there to derive the null controllability.More precisely,they were applied to the adjoint equation after the coordinate transformationx→y,which requiresC1or the Lipschitz condition on the coefficients in the principal part.This means that the geometric assumptions(A1)–(A2)are almost necessary to establish the existence results.
Since,as far as we know,there is no negative result for the null controllability in the case of parabolic equations with bounded and coercive coefficients,we expect that the null controllability operates under much weaker assumptions than(A1)–(A2).
Let us introduce the following notation:For givenλandsas in Theorem 2.1,we set

and

As consequence of Theorem 2.1,we have the following lemma.
Lemma 2.2Consider the same notations as in Theorem2.1.For λ,s≫0,the solutions u,v of(2.9)satis fiy the estimate:


Theorem 2.2Consider the hypotheses of Lemma2.2and assume,moreover,that there exists a constant b0>0and a domain ωbsuch that

and

for some T0>0.Then for all r∈[0,2)there exists a constant C=C(r,T,λ)such that

for all ω′satisfying


where
Assume for example thatb≥b0>0 inωb×(0,T)and introduce the functionFor real numbersβ0,β1,pandq>0,which will be chosen,set

In the other case−b≥b0>0,we modify the termtoin the expression for Γ.
Differentiating Γ with respect totand replacingutandvtby their expressions given by(2.9),we obtain

Hence,integration from 0 tot≤Tand using Γ(0)= Γ(T)=0(becauseα(0)=0,α(T)=−∞;see(2.10))yield

Next we estimate the above four integrals separately.
Estimate for J1In fact,sincewe introducer∈[0,2)and write e2α=e(2−r)αerα.Assuming that

and thatβ0,β1≥1,by using the Cauchy-Schwarz inequality,we get


whereC=C(p,q,|η|∞)and
Estimate for J2We have

where we have used the inequality(1.9).
Set

Derivate the integralN1with respect towe find 8 terms,namely:

In the following,we estimate each of these terms.
From the de finition ofη=ξ6,we obtain


It follows from this last computation and the assumptions(A1)–(A2)that

where
Plugging these estimates intoN1,we get

Proceeding as previously,we obtain


Also,

On the other hand,

and thus

Substituting(2.30)–(2.31)and(2.33)into(2.26)we have

Estimate for J3We have


Next,we bound from above the fifth and the second terms on the right-hand side of(2.35),respectively,as follows:

where we have used in(2.36)that

Similarly,

Substituting(2.36),(2.38)into(2.35),we obtain


Estimate for J4We have

From(2.25),(2.34),(2.39)and(2.40)applied to(2.23),we obtain

But fixing now

we obtain


Besides,we also have used in(2.43)that
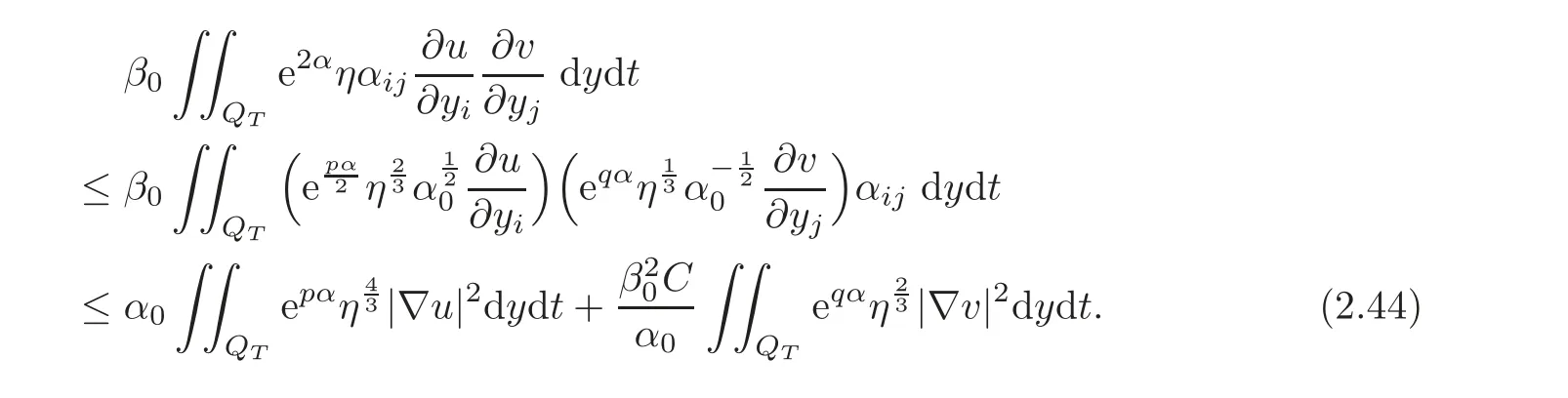
Analysis of the Terms in(2.43)We have

Also

because
Also,and finally,we have


Combining(2.45)–(2.47)with(2.43)and again with(2.42)yields

Select

By using(2.24)and(2.49)in the last inequality(2.48)we obtain

From the de finition ofξ(y)given in(2.20),we obtain

Sincer<2,α<0,then

This completes the proof of Theorem 2.2.
Note that if we modify the expression of functional Γ(t)de fined in(2.21)by takingsαinstead ofα,s>s0>0,we have the following result.
Corollary 2.1As an immediate consequence of Theorem2.2,it follows that for all r∈[0,2),there exists a constant C=C(r,T)such that
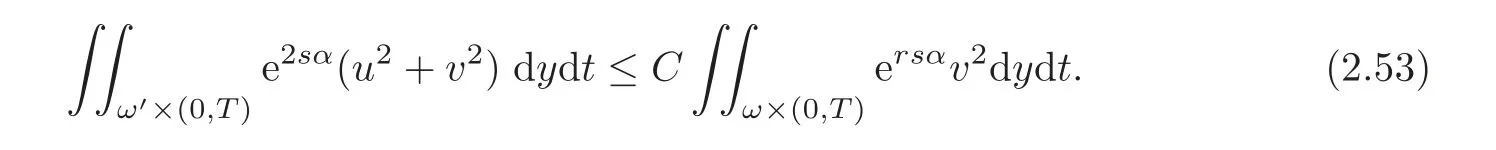
Now,we will prove the observability inequality for weak solutions of the adjoint system(2.9).Observe that it is a consequence of the Carleman inequality proved in Theorem 2.1 and Corollary 2.1.
Theorem 2.3Let the assumptions of Theorem2.2be satis fied.Then there exists a positive constant C depending on T,s and λ,such that every pair of solutions u=u(y,t),v=v(y,t)to(2.9)satis fies

wheresandλare taken as in Theorem 2.1.
ProofBy the Carleman inequality(Theorem 2.1),we have

for all,ands≥s0.If we setω=ω′(withω′as in Theorem(2.2))in(2.55),we have

We have

because
By using Corollary 2.1 and(2.56)–(2.57)we obtain

On the other hand,we also have

because
Combining(2.58)–(2.59)yields

Multiplying both sides of the first equation of(2.9)byuand integrating on Ω,and multiplying both sides of the second equation of(2.9)byvand integrating on Ω,we obtain

Recalling the assumptions(A1)–(A2)and using(2.5)and(1.9),we rewrite(2.61)and obtain

Thus

Employing(2.60)and(2.63)we finally obtain

Theorem 2.4Assume that b satis fies the same assumptions(2.17)–(2.18)as in Theorem2.2.For each ψ0,w0∈L2(Ω),there exists a control g∈L2(ω×(0,T))such that the weak solution ψ=ψ(y,t),w=w(y,t)of the state equation(2.8)satis fies

with an estimate for the control of the form

ProofWe prove this theorem by using a variational method and the observability inequality(see(2.54)).Forg∈L2(QT),r∈[0,2)and∈>0 given,let us introduce the functionalJ∈by

Here,the pairψ,wis the solution of(2.8)associated to the initial dataψ(T),w(T).It is not difficult to check thatJ∈is continuous,strictly convex and coercive inL2(QT),so it possesses a unique minimumg∈∈L2(QT),whose associated solution is denoted byψ∈,w∈.
We findg∈∈L2(QT),and by means of the state equation(2.8),we find the weak solutionψ∈,w∈.The next step consists in proving the convergence ofg∈,ψ∈andw∈,that is,

And the further step consists in proving that the pairψ,wis the weak solution of(2.8)corresponding to the controlgand that

Initially,we observe that by the maximum principle(or see,for instance,[9])we obtain that

where the pairu∈,v∈is the weak solution of the parabolic problem:

withψ∈,w∈being the solution of

Recall that our objective is to show thatψ∈(y,T)=0 and,w∈(y,T)=0 in Ω.For this,we need to estimate the functionsg∈and the pairψ∈,ω∈in order to assure the convergence ofg∈togandψ∈,ω∈toψ,ωas∈goes to zero.In the following,we describe how to obtain such estimates.As the first step,multiply both sides of the first equation of(2.71)byψ∈and both sides of the second equation of(2.71)byw∈,and integrate onQT.As the second step,multiply both sides of the first equation of(2.71)byu∈and both side of the second equation of(2.71)byv∈,and integrate onQT.Adding the results of these steps,we obtain

By the inequality of observability for(2.71)(see Theorem 2.3),we obtain from(2.71)and(2.73):


Thus from(2.74)we obtain

from which it follows that

Also from(2.74)we have

From(2.72)we obtain

Applying a compactness result(see,for example,Lions[18]),we can extract a subsequence of(ψ∈),(w∈),which shall still be represented by(ψ∈),(w∈),such that

It is easy to see that the limitgis such that the solutionψ,wof the system

satis fies(2.65).
Moreover,by the lower semi-continuity of the norm with respect to the weak topology and in view of(2.76)–(2.79),we deduce that(2.66)holds.This completes the proof of Theorem 2.4.
3 Null Controllability of the Nonlinear Problem
This section is devoted to proving the main result in this paper,namely,Theorem 1.1.By the inverse mappingτ−1,we prove that Theorem 3.1 below implies Theorem 1.1.For this reason,we only need to prove Theorem 3.1.It will be a consequence of Theorem 2.4 and Kakutani’s fixed-point theorem.
Remark 3.1The system(1.1)is to be said locally null controllable at timeTif the previous property holds for anyψ0,w0in a ballB(0;δ)⊂L2(Ω),withδdepending onT.
Theorem 3.1Assume that the conditions of Theorem1.1hold.Then for any ψ0,w0in a ball B(0;δ)⊂L2(Ω),with δ depending on T,the nonlinear system(1.8)is locally null controllable at time T.
More precisely,for any ψ0,w0in a ball B(0;δ)⊂L2(Ω),with δ depending on T and T>0,there exists a control g∈L2(ω×(0,T))such that the solution ψ,w of(1.8)satis fies

ProofWe apply the fixed point method,as is usually done.As we will work with the multi-valued function,we need an in finite dimensional version of Shizuo Kakutani’s fixed point theorem.In order to do this,we introduce the following Hilbert space:

which is equipped with the norm

(see,for instance[18]).We observe that

Let us fixR>0 and denote byB=B(0,R)the closed ball inW×Wof center 0 and radiusR.Hence,Bis a convex and compact subset of
For eachwe consider the null controllability problem for

wherea,b,canddare given in(2.2)–(2.3).
In view of(1.3)and Theorem 2.4,there exists a controlsuch that the associated stateψ,wsatis fies(2.65)–(2.66).
We de fine the mapping Φ :as follows:Forwe set,by de finition
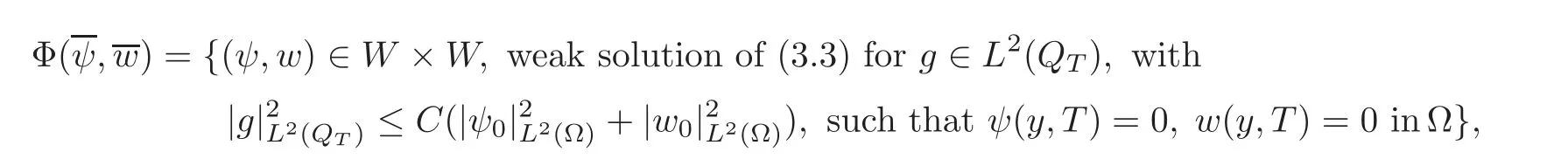
Then,the goal is to prove that the multi-valued mapping Φ satis fies the hypotheses of Kakutani’s fixed-point theorem.
We consider.Thenis non-empty and convex(a consequence of Theorem 2.4).Let us now prove that Φ :that is,Φ(B)⊂B.In fact,for allifby the de finition ofis a weak solution of(3.3).
By the same argument to obtain(2.62),which is applied to(3.3),we obtain

Thus
Hence


where
Fix anywithFrom the first equation of(3.3)and by using Poincaré’s inequality,assumptions(A1)–(A2)and the estimate(2.5),we obtain

and thus

Again,using(3.5)yields

By a similar argument we obtain finally

We observe thatC2andC5depend onandT.
Thus,ifψ0,w0are sufficiently small,i.e.,if

then Φ(B)⊂B.
We claim now thatis closed inX.Indeed,letbe fixed inB,andsuch that:strongly inL2(QT)for alln.By the de finition ofwe have

with
We extract a subsequence(gn)n∈Nsuch that

By the same argument to obtain(3.10)from(3.3),we get

or

From(3.14)we extract a subsequencesuch that

We have assured the last two convergence by Aubin-Lions compactness result;see,for example,Lions[18](or equivalently,as a consequence of the compactness of the embedding ofintocf.(3.2)).
From(3.13)and(3.16),we pass to the limits in(3.12)asn→∞and obtain

andThus,andis closed inX.
Thus,sinceBis a compact ofXand Φ(ψ,w)⊂Bis closed,it implies thatis a compact ofX.
We now intend to show that Φ has the closed graph inX×X.This is not difficult to check:Assume thatstrongly inXandstrongly inX,withfor alln.It remains to show thatIn fact,fromit follows that(ψn,wn)is a weak solution of the following problem:

with
Recall(see,e.g.,(3.15)or equivalently(3.14))that the following energy inequality holds for(3.18):

By Aubin-Lions compactness theorem(see(3.3))and using thatstrongly inX×X,we can derive the estimates similar to(3.16)for the sequenceof a weak solution of(3.18).They are as follows:

Notice that by hypothesis we have

From the convergences above,passing to the limits in(3.18)asit is then easy to see that
Therefore,the multi-valued mappingsatis fies the conditions of Kakutani’s fixed-point theorem,which are:Bis a non-empty convex compact set,and Ψ has a closed graph inX×X.Hence it has a fixed point.The proof of Theorem 3.1 is complete.
AcknowledgmentsThe authors thank the anonymous referees for their important suggestions and observations which made our paper more understandable.The co-authors dedicate this paper to Prof.Silvano for his premature death.
[1]Benabdallah,A.and Naso,M.G.,Null controllability of a thermoelastic plate,Abstr.Appl.Anal.,7,2002,585–599.
[2]Bernardi,M.L.,Bonfanti,G.and Lutteroti,F.,Abstract Schrödinger type differential equations with variable domain,J.Math.Ann.and Appl.,211,1997,84–105.
[3]Cabanillas,V.R.,De Menezes,S.B.and Zuazua,E.,Null controllability in unbounded domains for the semilinear heat equation with nonlinearities involving gradient terms,J.Optm.Theory Appl.,110(2),2001,245–264.
[4]Chen,G.Q.and Frid,H.,Divergence-measure fields and hyperbolic conservation laws,Archive Rat.Mech.Anal.,147(2),1999,89–118.
[5]Cooper,J.and Bardos,C.,A nonlinear wave equation in a time dependent domain,J.Math.Anal.Appl.,42,1973,29–60.
[6]De Menezes,S.B.,Limaco,J.and Medeiros,L.A.Remarks on null controllability for semilinear heat equation in moving domains,Eletronic J.of Qualitative Theory of Differential Equations,16,2003,1–32.
[7]Doubova,A.,Fernández-Cara,E.,González-Burgos,M.and Zuazua,E.,On the controllability of parabolic systems with a nonlinear term involving the state and the gradient,SIAM J.Control Optim.,41(3),2002,798–819.
[8]Fabre,C.,Puel,J.P.and Zuazua,E.,Approximate controllability of the semilinear heat equation,Proc.Royal Soc.Edinburgh,Ser.A,125,1995,31–61.
[9]Fernández-Cara,E.and Guerrero,S.,Global Carleman inequalities for parabolic systems and applications to controllability,SIAM J.Control Optim.,45(4),2006,1395–1446.
[10]Fernández-Cara,E.and Zuazua,E.,Null and approximate controllability of weakly blowing-up semilinear heat equations,Ann.Inst.Henri Poincaré,Analyse non Linéaire,17(5),2000,583–616.
[11]Fursikov,A.and Imanuvilov,O.,Controllability of evolution equations,Lecture Notes,Vol.34,Seoul National University,Korea,1996.
[12]González-Burgos M.and Pérez-García R.,Controllability results for some nonlinear coupled parabolic systems by one control force,Asymptot.Anal.,46(2),2006,123–162.
[13]He,C.and Hsiano,L.,Two dimensional Euler equations in a time dependent domain,J.Diff.Equations,163,2000,265–291.
[14]Imanuvilov,O.Yu.,Controllability of parabolic equations(in Russian),Mat.Sbornik.Novaya Seriya,186,1995,109–132.
[15]Inoue,A.,Sur□ut+u3=fdans un domaine non-cylindrique,J.Math.Anal.Appl.,46,1970,777–819.
[16]Khodja,F.,Benabdallah,A.and Dupaix,C.,Null controllability of some reaction-diffusion system with one control force,J.Math.Anal.and Appl.,320,2006,928–943.
[17]Khodja,F.,Benabdallah,A.,Dupaix,C.and Kostin,I.,Controllability to the trajectories of phase- field models by one control force,SIAM J.Control Optim.,42(5),2003,1661–1680.
[18]Lions,J.L.,Quelques méthodes de résolution des problèmes aux limites non-linéaires,Dunod,Paris,1960.
[19]Lions,J.L.,Une remarque sur les problèmes d’evolution nonlineaires dans les domaines non cylindriques(in French),Rev.Roumaine Math.Pures Appl.,9,1964,11–18.
[20]Medeiros,L.A.,Non-linear wave equations in domains with variable boundary,Arch.Rational Mech.Anal.,47,1972,47–58.
[21]Miranda,M.M.and Limaco,J.,The Navier-Stokes equation in noncylindrical domain,Comput.Appl.Math.,16(3),1997,247–265.
[22]Miranda,M.M.and Medeiros,L.A.,Contrˆolabilité exacte de l’équation de Schrödinger dans des domaines non cylindriques,C.R.Acad.Sci.Paris,319,1994,685–689.
[23]Nakao,M.and Narazaki,T.,Existence and decay of some nonlinear wave equations in noncylindrical domains,Math.Rep.,XI-2,1978,117–125.
 Chinese Annals of Mathematics,Series B2016年1期
Chinese Annals of Mathematics,Series B2016年1期
- Chinese Annals of Mathematics,Series B的其它文章
- Solution of Center-Focus Problem for a Class of Cubic Systems∗
- Kinematic Formulas of Total Mean Curvatures for Hypersurfaces∗
- Constructing Invariant Tori for the Spatial Hill Lunar Problem
- The Pointwise Estimates of Solutions to the Cauchy Problem of a Chemotaxis Model∗
- Characterization of Groups L2(q)by NSE Where q∈ {17,27,29}∗
- A Note on Model(Co)slice Categories∗
