The Pointwise Estimates of Solutions to the Cauchy Problem of a Chemotaxis Model∗

Renkun SHI Weike WANG

1 Introduction

Chemotaxis is a phenomenon describing the movements of bacteria or cells in response to some chemical substances.According to the orientation of the movements,we can describe the phenomenon by attractive chemotaxis and repulsive chemotaxis,respectively.The former occurs when the movement is toward a higher concentration of the chemical,and conversely,the latter occurs when the movement is in the opposite direction.One famous attractive chemotaxis model named Keller-Segel model was proposed by Keller and Segel[3]in the 1970s describing the aggregation process of amoebae by chemoattraction.In[9],Luca proposed a more general attraction-repulsion chemotaxis model to describe the aggregation of microglia and formation of local accumulations of chemicals observed in AD senile plaques.In this paper,we consider the following attraction-repulsion chemotaxis system(ARC):

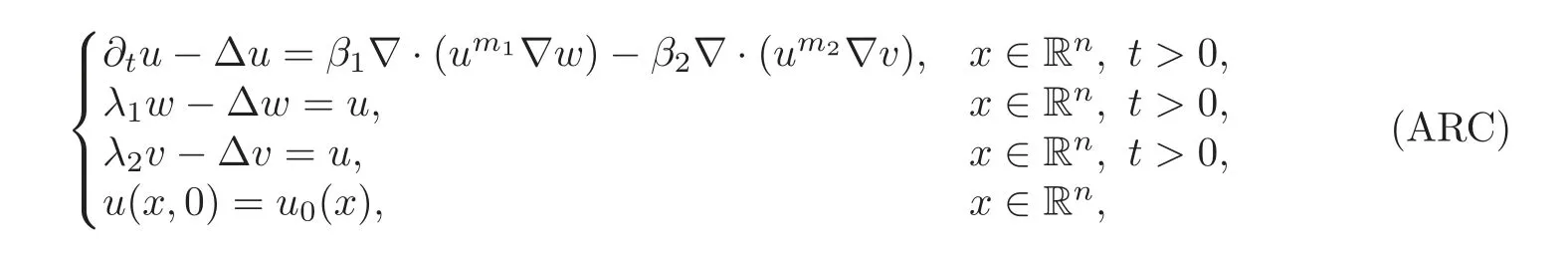
where the spatial dimensionn≥1,u(x,t)denotes the density of cells,denotes the concentration of chemorepellents,andv(x,t)denotes the concentration of chemoattractants;the parametersβ1andβ2represent the sensitivities of cells to the chemorepellents and the chemoattractants respectively;are positive parameters andare positive integers.The aim of this paper is to show the pointwise estimates of solutions to the system for small initial data and to obtain the decay rates of solutions inWs,p(Rn)space.

Whenβ1=0,this model is just the well-known simpli fied Keller-Segel(KS)model,for which a number of works were carried out from various viewpoints.For these background knowledge and more information,we refer to[2,10–11]and their references.We mention here some related works for the(KS)model with small initial data.In[14],Y.Sugiyama and H.Kunii proved that a global solution exists for the(KS)model with small initial data and obtained thedecay rates of the solution.Forn≥3 andm2=1,H.Kozono and Y.Sugiyama[4]considered local and global existence for the(KS)model with initial datanand proved the existence of strong solution withfor

Whenβ1,β2＞0,because of the interaction of the two attraction and repulsion effects,the(ARC)model can represent much richer phenomena.When the repulsion prevails over the attraction,that is,whenβ1＞β2,one can expect the global existence of solutions for large initial data,while whenβ1＜β2,the finite time blow-up may occur.Such results can be seen in[15]where the authors considered the system(ARC)form1=m2=1 in a bounded domain.For other results of the attraction-repulsion chemotaxis model,we can refer to[6,12]and the references therein.In this paper,we are interested in the Cauchy problem of the system(ARC)with small initial data.We prove that no matter in what parameter regime,the system(ARC)is always globally solvable for small initial data.More precisely,we study the pointwise estimates of solutions to the system,which is very helpful for us to better understand the behaviors of solutions to the system in both time and space.And we also derive theWs,p(Rn)decay rates of solutions to(ARC).

For getting the precise pointwise estimates,to the authors’best knowledge,Green’s function is one of the most effective tools to describe the pointwise estimates.In[8],Liu and Zeng investigated the pointwise estimates of solutions to general hyperbolic-parabolic systems in one space dimension.D.Hoffand K.Zumbrun[1]considered pointwise decay estimates for multidimensional Navier-Stokes equations with an arti ficial viscosity term.Then Liu and Wang[7]used the Green’s function method in odd multi-dimensional Navier-Stokes equations,obtained long time behavior of solutions under small perturbation and proved the generalized Huygen’s principle.After that more work involved in this field was done.

Most of the papers mentioned above are about hyperbolic-parabolic systems.For the hyperbolic-parabolic-elliptic coupled type,there are also some results recently(see[5,16]).However,after the transformation of their systems,the elliptic effect is re flected in the nonlocal linear term,while for the system(ARC),the nonlocal term is nonlinear,which is a difficult point to deal with in this paper.Actually,we can solve the second and the third equations in(ARC)with the help of Bessel potentialsThen we can easily get the boundedness estimates ofwandvin the norms ofuby the knowledge of pseudo-differential operators,while for the more precise estimates,such as pointwise estimates,we cannot obtain them so easily.Thus we must make more delicate calculations in our study.We shall show them later.

Before we show our results,we give some notations that are frequently used in the paper.

NotationsThroughout the paper we denote generic constants byCwhich may vary line by line according to the context.Ws,p(Rn)andLp(Rn)represent the usual Sobolev spaces and theLp(Rn)norm of a function is denoted byFor any multi-indexesα=we denoteWe also denotewith

where

is the fundamental solution to the heat equation.The expression(1.1)of the kernel of Bessel potential can be seen in[13,Chapter V,Section 3.1].We also denote

for anywhich can be seen as some substitution of the function e

The main results of this paper are stated in the following.

Theorem 1.1Let(u,w,v)be the solutions to the Cauchy problem(ARC).Then there exists∈＞0,such that if u0(x)satis fies

whereand h is a given positive integer,then we have the estimate

for all t≥0,|α|≤h.a(∈)depends on n,h,r,∈and the parameters in the equations.w(x,t)and v(x,t)satisfy the same estimates as(1.5).

Corollary 1.1Let(u,w,v)be the solutions to the Cauchy problem(ARC),and u0∈Ws,p(Rn),where s＞0is an integer,p∈[1,∞].Then there exists∈＞0,such that if u0(x)satis fies

wherethen we have the estimate

for all t≥0,|α|≤s.a(∈)depends on n,s,r,∈and the parameters in the equations.w(x,t)and v(x,t)satisfy the same estimates as(1.7).

From Theorem 1.1 and Corollary 1.1,we can conclude that both the attraction and repulsion effects can be dominated by the diffusion term under the smallness condition,and therefore the behavior of solutions is similar to the heat equation.We also state that our global existence result and decay rates of solutions are independent of the parametersmiandβi(i=1,2)and the signs ofβi(i=1,2).

For simplicity and convenience to carry on in this paper,we transform the system(ARC)into the following form:

We investigate the pointwise estimates andWs,p(Rn)decay rates of solutionu(x,t)to the problem(1.8),and we can prove that the solutions to the original system(ARC)satisfy the same estimates.In deriving these results,we also omit the proof of some lemmas to make this paper brief.

The rest of the paper is arranged as follows.In Section 2,we shall give some lemmas which are very useful for the proof of the main theorem.The pointwise estimates of solutions will be carried out by Duhamel’s principle in Section 3.

2 Some Lemmas

In this section,we shall give some lemmas which will be used in proving the main theorem in the next section.

Lemma 2.1Ifand n3=min{n1,n2},then

where C depends only on n1,n2and n.

The proof of Lemma 2.1 can be seen in[17].

Lemma 2.2Assume that G is the heat kernel given by(1.2),and f(x)satis fies

and

for some

multi-indexes α∈Znand Then we have

where C depends only on n,m and α,and Bm(|x|,t)is de fined by(1.3).

ProofWhent≥1,we can easily deduce

Then by(2.2)and Lemma 2.1,it holds that

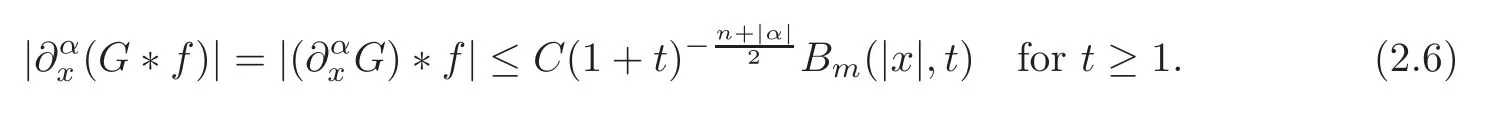
Whent≤1,it follows from(2.3)that

Now denote

Ifit holds that

and if|x−y|≤1,it holds that

Therefore,wheny∈I,we always have

hence

Else ifthen we have

Therefore,we can deduce

where we have also used the fact oft≤1.The corresponding integral satis fies

whereFrom(2.7),(2.12)and(2.15),we can bound the whole integral:

By(2.6)and(2.16),we complete the proof.

To obtain the precise estimates of the nonlocal terms of equation(1.8),we next give a very useful lemma which plays an important role in our proof of the theorem.

Lemma 2.3If

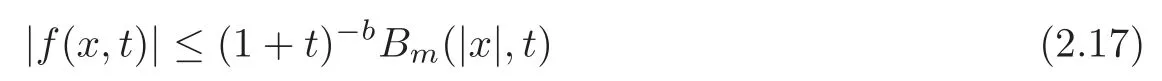
for some nonnegative constant b andthen

where C depends only on n,m and λ,Kλis given by(1.1)and Bm(|x|,t)is de fined by(1.3).

ProofWithout loss of generality,we takeb=0.

We first make estimates for I1.Sinces＞1,we have

Then it follows from Lemma 2.1 that

For I2,1,since|y−x|≤1,it naturally holds that

so

which implies

And for I2,2,noticing thats∈[0,1]and|y−x|≥1,we have

that is

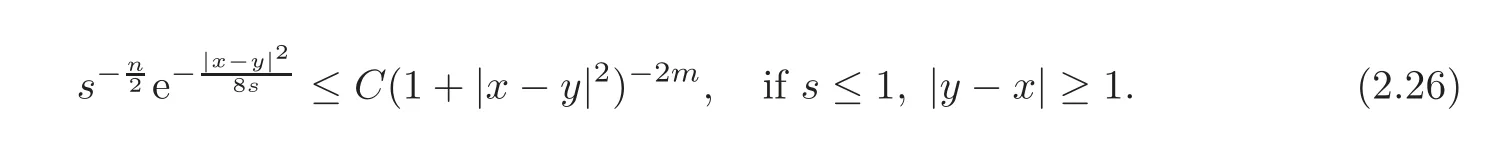
Then by Lemma 2.1,we can get

Combining all the estimates of above,we complete the proof.

The next lemma is also very important for our proof,which deals with the nonlinear parts in the equation.

Lemma 2.4If

wherethen we have

ProofBecause of the singularity of the functionatt=0,we divide the integrating range into several parts and study them respectively.We have

From the conditions(2.28)and(2.29),we have

and

We consider P first and study it in two different cases:t≥1 andt≤1.Whent≥1,noticing thatthe following holds:

Therefore,it follows from(2.32)that

Ifit is easily shown that

so

Else ifwe have estimates

and

where we have also used the fact of(2.39)–(2.40)imply

for.Substituting(2.41)into(2.36)and noticing thatwe get

Combining(2.38)and(2.42),we have

Now let us consider the other caset≤1 for P.In this case,the following estimates hold:

where(2.44)and(2.45)can be proved in exactly the same way as(2.23)and(2.26),alternatively.We mention that(2.44)always holds for anyt≥s≥0 if|y−x|≤1.From(2.33)and(2.44)–(2.45),we can obtain

By using Lemma 2.1,we can get

Combining(2.43)and(2.47),we have

Next we consider the other term Q.Obviously,from(2.34),we have

For Q1,it follows from(2.44)that

For Q2,whent≤1,it follows from(2.45)that

where we have also used Lemma 2.1.Whent≥1 and|x|2≤t,by virtue of(2.37),we have

And when|x|2≥t≥1,we follow(2.41)and Lemma 2.1 to derive

Then it follows from(2.51)–(2.53)that

Combining(2.49)–(2.50)and(2.54),we have

Finally,from(2.48)and(2.55),we obtain

The proof is complete.

3 Proof of the Main Theorem

Now,we can prove Theorem 1.1 on the basis of the above lemmas.

Proof of Theorem 1.1By(1.8)and Duhamel’s principle,the solutionucan be expressed by the formula

Therefore,we consider the following successive approximation forms:

where

Let

where

From the assumption and Lemma 2.2,it holds that

By Lemma 2.3,we have

and obviously,

Then by Lemma 2.4,we have

(3.2),(3.5)and(3.8)yield

Recall the prior assumption(3.3),which holds that

Now choose∈sufficiently small such that the equationhas a positive solutiona(∈)satisfyingThen we have the following uniform estimate:

Therefore,

Next we show thatis a Cauchy sequence inLp(Rn)for 1≤p≤+∞.Let

and

By(3.2),we have

Let

Then from(3.12)–(3.13),we can deduce that

that is

with

Take∈sufficiently small,such that

which yields thatis a Cauchy sequence inTherefore,there exists a limitthat satis fies

Now lettingin(3.2),we see thatu(t,x)satis fies(3.1).By induction and a similar process,we can prove thatis also a Cauchy sequence inLp(Rn)for every 1≤p≤+∞and|α|≤hand the limit is obviously the weak partial derivative ofu(x,t).Finally,from(3.12)we obtain

By Lemma 2.3,the solutionsw(x,t)andv(x,t)satisfy the same estimate as(3.14).The proof is complete.

AcknowledgementThe authors are grateful to the referees for their valuable comments and suggestions.

[1]Hoff,D.and Zumbrun,K.,Pointwise decay estimates for multidimensional Navier-Stokes diffusion waves,Z.angew.Math.Phys.,48,1997,1–18.

[2]Horstmann,D.,From 1970 until present:The Keller-Segel model in chemotaxis and its consequences,I.Jahresber.Deutsch.Math.-Verien,105(3),2003,103–106.

[3]Keller,E.F.and Segel,L.A.,Initiation of slime mold aggregation viewed as an instability,J.Theor.Biol.,26,1970,399–415.

[4]Kozono,H.and Sugiyama,Y.,Strong solutions to the Keller-Segel system with the weakLn2initial data and its application to the blow-up rate,Math.Nachr.,283(5),2010,732–751.

[5]Li,H.L.,Matsumura,A.and Zhang,G.J.,Optimal decay rate of the compressible Navier-Stokes-Poisson system in R3,Arch.Ration.Mech.Anal.,196,2010,681–713.

[6]Liu,J.and Wang,Z.A.,Classical solutions and steady states of an attraction-repulsion chemotaxis in one dimension,J.Biol.Dyn.,6,2012,31–41.

[7]Liu,T.P.and Wang,W.K.,The pointwise estimates of diffusion wave for the Navier-Stokes systems in odd-multi dimensions,Comm.Math.Phys.,196,1998,145–173.

[8]Liu,T.P.and Zeng,Y.,Large Time Behavior of Solutions for General Quasilinear Hyperbolic-Parabolic Systems of Conservation Laws,Mem.Amer.Math.Soc.,125(599),Amer.Math.Soc.,Providence,RI,1997.

[9]Luca,M.,Chavez-Ross,A.,Edelstein-Keshet,L.and Mogilner,A.,Chemotactic singalling,microglia,and alzheimer’s disease senile plaques:Is there a connection?Bull.Math.Biol.,65,2003,673–730.

[10]Nagai,T.,Blow-up of nonradial solutions to parabolic-elliptic systems modelling chemotaxis in twodimensional domains,J.Inequal.and Appl.,6,2001,37–55.

[11]Nagai,T.,Syukuinn,R.and Umesako,M.,Decay properties and asymptotic pro files of bounded solutions to a parabolic system of chemotaxis in Rn,Funkcial.Ekvac.,46,2003,383–407.

[12]Perthame,B.,Schmeiser,C.,Tang,M.and Vauchelet,N.,Traveling plateaus for a hyperbolic kellersegel system with attraction and repulsion-existence and branching instabilitiesn,Nonlinearity,24,2011,1253–1270.

[13]Stein,E.M.,Singular Integrals and Differentiability Properties of Functions,Princeton University Press,Princeton,1970.

[14]Sugiyama,Y.and Kunii,H.,Global existence and decay properties for a degenerate Keller-Segel model with a power factor in drift term,J.Diff.Eqs.,227,2006,333–364.

[15]Tao,Y.S.and Wang,Z.A.,Competing effects of attraction vs.repulsion in chemotaxis,Math.Models Methods Appl.Sci.,23,2013,1–36.

[16]Wang,W.K.and Wu,Z.G.,Pointwise estimates of solution for the Navier-Stoks-Piosson equations in multi-dimensions,J.Diff.Eqs.,248,2010,1617–1636.

[17]Wang,W.K.and Yang,T.,The pointwise estimates of solutions for Euler equations with damping in multi-dimensions,J.Diff.Eqs.,173,2001,410–450.