Degenerate Nonlinear Elliptic Equations Lacking in Compactness
MariaCristian UDREA
1 Introduction
In[16],Motreanu andstudied the existence of solutions of the problem

involving the singular potentiala(x)under veri fiable conditions for the nonlinear termfwhenλ >0 is sufficiently small.Also,they studied a nonlinear eigenvalue problem for which they proved an existence result containing information about the location and multiplicity of eigensolutions.
The aim of the present paper is to extend the results obtained in[16]to degenerate elliptic equations of thep-Laplacian type.More precisely,here we study the existence of nontrivial weak solutions of the following problem

wherep>1 is a real number,ais a nonnegative weight,λis a positive real parameter and Ω is a(bounded or unbounded)domain in RN(N≥2).
The main interest of these equations is due to the presence of the singular potentiala(x)in the divergence operator.Problems of this kind arise as models for several physical phenomena related to equilibrium of continuous media which may somewhere be “perfect insulators” (see[9,p.79]).These equations can often be reduced to elliptic equations with the Hardy singular potential(see[17]).For further results and extensions,we refer to[1,3,7,10,20–22].
The growing attention for the study of thep-Laplacian operator Δpin the last few decades is motivated by the fact that it arises in various applications.For instance,in fluid mechanics,the shear stressand the velocity gradient∇puof certain fluids obey a relation of the formwhereThep-Laplacian also appears in the study of tensorial creep(elastic forp=2,plastic as(see[12]), flow through porous mediaor glacial sliding(see[18]).More details on this topic can be found in[13–15].
The proofs of our main results rely on an adequate variational approach where,in view of the presence of a singular potential and a(possibly)unbounded domain,the usual methods fail to apply.Since we are interested in the case of lacking compactness,we suppose Ω=RNand we do not make use of the Palais-Smale condition.The other cases when Ω⊂RNis unbounded can be treated similarly.Moreover,we employ an inequality due to Caldiroli and Musina[6](see also[5]for the casewhich extends the inequalities of Hardy[11]and Caffarelli et al.[4].
This paper is organized as follows.In Section 2 we de fine the suitable Sobolev weighted spaces and we present our main results.In Section 3 we prove the existence of solutions for our problems,using the mountain-pass theorem and a special version of it involving a suitable hyperplane.
2 Preliminaries and Main Results
Let Ω be a(bounded or unbounded)domain in RN,withN≥2,and leta:Ω→[0,∞)be a weight function satisfyingWe introduce the following assumptions:with a real numberα∈[0,∞);(if Ω is unbounded).
A model example isa(x)=|x|α.The caseα=0 covers the “isotropic” case corresponding to the Laplace operator.
For anywe set

Letandbe the closures ofwith respect toandrespectively.Clearly we havewith continuous embedding.
For anyα∈(0,p),we denote

Lemma 2.1(see[6])Assume that the functionsatis fies conditions(hα)andfor some α∈(0,p).Then there exists a positive constant C such that

for any
In order to simplify the arguments,we admit throughout the paper thatfor someα∈(0,p),and thatλ>0.Since we are interested in the case of lacking compactness,we suppose Ω=RN.
In the present paper,we deal with the following nonlinear elliptic equation

We assume thatp>1 is a real number and the nonlinearityin(2.1)is continuous and satis fies the following hypotheses:
(H1)f(x,t)≥0 for allt≥0;f(x,t)≡0 for allt<0,x∈RN;

(H3)the mappingis of classC1;and there exists thefor allx∈RN;
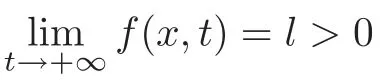
(H5)for anyM>0,there existsθ>0 such that


(H6)there existsη>0 such that


(H7)the functionf(·,t)is bounded from above uniformly with respect totbelonging to any bounded subset of R+.
Remark 2.1A useful consequence of assumptions(H1)–(H3)is that the derivative with respect totof the mappingvanishes att=0 uniformly inx∈RN.Indeed,we haveuniformly inx∈RN.
Moreover,without loss of generality,we may suppose that
Remark 2.2It is easy to see that the assumption(H5)ensures

Indeed,becauseM>0 is arbitrary andθF(x,t)≥0 for allx∈RNandt≥0,we easily obtain the above relation.
Remark 2.3Assumption(H7)can be applied when the functionis nondecreasing for allx∈RN.It is so,because(H4)then implies(H7).
One of the main results of this work is given by the following theorem.
Theorem 2.1Assume that conditions(H1)–(H7)are ful filled.Then problem(2.1)has a nontrivial weak solution for every λ∈(0,l),where l>0is the constant in(H4).
In the sequel,for anywe set

Letdenote the space obtained as the completion ofwith respect to the-norm.LetEbe the space de fined as the completion ofwith respect to the norm

De finition 2.1We say that a function u∈E is a weak solution of problem(2.1)if

for all
Remark 2.4We are working withinstead ofbecause in our approach,it is essential to keep the support of the test functions away from 0 exploiting that every bounded sequence in the spacecontains a strongly convergent subsequence in
Proposition 2.1is a re flexive Banach space.
The proof of this result follows the same ideas as in the case of Sobolev spaces(see,for instance,[8]).
Remark 2.5We clearly havewith continuous embedding.
Remark 2.6If Ω is a bounded domain in RNandthen the embeddingis compact forwhereMoreover,we deduce thatis compactly embedded inLi(Ω)for any
In the sequel,we give our second main result,namely,a related nonlinear eigenvalue problem corresponding to the degenerate potentialwithα∈(0,p).
Fix a positive numberν>0 and letbe aC1function satisfying the following conditions

with constants



The notationin(2.5)means the weak convergence.
Problem 2.1Find an eigensolutionsuch that

with fixed constantsα>0 andλ>0.The concept of solution in(2.6)is clearly compatible with De finition 2.1.
Due to the fact thatin(2.2),a solutionu∈Eof(2.6)is necessarily nontrivial,that is,u∈E{0}.Assume further that

that is,(2.6)is not solvable forOur main result in studying problem(2.6)is the following.




3 Proofs of Main Results
In this section,we give the proofs of our main results which are Theorem 2.1 and Theorem 2.2.
The basic idea in proving Theorem 2.1 is to consider the associate energetic functional of(2.1)and to show that it possesses a nontrivial critical point.
We de fine the energetic functional associated to problem(2.1)asJ:E→R,where

A straightforward argument based on Lemma 2.1,Remark 2.5 and assumptions(H1)–(H4)shows thatJis well-de fined on the spaceEand is of classC1(E,R),with the derivative given by

for allu,v∈E.Thus,using De finition 2.1,we observe that the weak solutions of(2.1)correspond to the critical points of the functionalJ.
Lemma 3.1Suppose that(H1)–(H4)are ful filled.Let(un)⊂E be a sequence such that for some c∈R,one has and asIf there exists u0∈E such that,then and thus u0is a weak solution of(2.1).
ProofUsing Remarks 2.5–2.6,we may assume thatinLp∗α(ω),for all bounded domainωin RNwith 0/∈ω.
If we prove that

then by the fact thatandasis a weak solution of(2.1).
Therefore,we consider an arbitrary bounded domainωin RNwithand an arbitrary functionsuch that
The convergence

implies

that is,

SinceinE,it follows that

Next,we show that

Indeed,becauseby Remark 2.6,we have

By Remark 2.1,we obtain that

and by(H4),we have

uniformly inx∈RN,t≥0,where the last limit exists due to(H3)in conjunction with(H4).
Then for everyε>0,there exists a positive constantCεsuch that

In the above inequality,we essentially used that the derivativeis continuous,and is thus bounded on any compact set in RN×R.
As known from(3.4),.Then,passing,if necessary,to a subsequence,there is a functionsuch thatinω.Using(3.7)and the Hölder inequality,we obtain

for alln∈N.Thus,we obtain relation(3.3).Therefore,from(3.1)–(3.3),we deduce that

Finally,the density ofinEensures thatwhich finishes the proof.
Remark 3.1Lemma 3.1 holds,assuming in(H1)–(H4)that the convergence is uniform only on the bounded subsets of RN.
In order to prove thatJhas a nontrivial critical point,our idea is to show that actuallyJpossesses a mountain-pass geometry.So,we have the following auxiliary results.
Lemma 3.2Assume that the conditions(H1)–(H4)and(H7)hold.Then there exist constants ρ >0and a>0such that for all u∈E with‖u‖=ρ,one has J(u)≥a.
ProofBy(H1)–(H4),it follows that for anyσ>0,uniformly with respect tox∈RN,it is true that

In particular,we have

and for anyσ′>p,

Takingimplies

Using(3.9)and(3.11),we obtain that for everyε>0,there exist constants 0<δ1<δ2such that uniformly with respect tox∈RN,the following estimates hold:

Assumption(H7)guarantees thatFis bounded on RN×[δ1,δ2].We deduce that there exists a positive constantCεsuch that

Then(3.12)and Lemma 2.1 show that


Remark 3.2Using the same techniques as in the proof of(3.12),due to assumptions(H1)–(H4)and(H7),we may conclude that for anyε>0,there exists a positive constantDεsuch that


In the sequel,we construct an important element of the spaceE.Let us denote

and for an arbitrary numbera>0,

Proposition 3.1The function wasatis fies wa∈E whenever a>0.
ProofFixa>0 and de fine

It is enough to show thath∈E.We have to establish that for anyε>0,there isψ∈such thatFirst we prove that,for everyε>0,there exists a functionsuch that

Given any numberwe have

We derive that a positive constantc=c(z)can be found with the property thatfor all

We check that there exists some constantδ>0 such that

So we have

whereωNis the surface measure of the unit sphere in RN.To this end,we note that the below equality holds

Then using(3.18)for,we have

with a positive constantTo obtain(3.19),it is enough to choose


Using(3.19)and takingδsufficiently large,we find two positive constantsC1andC2satisfying

Settingfrom the above relations,it follows that

SinceC1+C2is independent ofε,it turns out that

Fix now a functionsuch that

Then,combining the above two relations,we arrive at the conclusion of Proposition 3.1 and if nish the proof.
Lemma 3.3If the conditions(H1)–(H4),(H7)hold and λ∈(0,l)with the number l in(H4),then for the positive number ρ given in Lemma3.2,there exists e∈E such that‖e‖ >ρ and J(e)<0.
ProofFix the elementwa∈Ein Proposition 3.1 for somea>0.From(3.14),we easily get

Using(3.15)and the above relation,we obtain

Next,using the notationd(N)entering the formula ofwa,we introduce

We easily get

Then,we find

Recalling that 0<α<pand making use of the assumption 0<λ<l,we choose

One obtains

Sinceand by(H4),

it follows that

Using Fatou’s lemma(see[8,Theorem 1.15–2]),we get

In particular,we obtainasIft0>0 is large enough ande=t0wa,we achieve the conclusion of Lemma 3.3 withe=t0waand the proof reaches an end.
Proof of Theorem 2.1Let us introduce the set

whereEis the space described in Section 2 ande∈Eis determined by Lemma 3.3.Moreover,we consider

Due to Lemma 3.3,we know thatso every pathγ∈Γ intersects the sphereConsequently,Lemma 3.2 implies

with the constanta>0 in Lemma 3.2,soc>0.
By the mountain-pass theorem(see,e.g.,[2]),we obtain a sequence(un)⊂Eso that

Firstly,we show that(un)is bounded inE.Indeed,from the first convergence in(3.28)we have

We note that

By(H6),there exist constantsC>0 andM>0 such that

Corresponding to the numberM>0 in(3.31),by(H5)there exists some constantθ>0 such that

Thus,by taking into account(3.29)–(3.30),we find

Due to(3.33),together with(3.32)and Remark 2.2,we obtain

On the other hand,using(3.29)–(3.30),it follows that

Then,from(3.31)and Remark 2.2,we have

Thus,for a constantc0>0,we infer that

Relations(3.13)and(3.34)ensure

Taking into account the expressions ofandσin(3.13),it follows that

Consequently,using the Hölder inequality,Lemma 2.1 and(3.37),we obtain that there exists a constantdepending onεand a constantC>0 such that

Fix

Recalling that(according to the second relation in(3.28)),the above inequality shows that(un)is bounded.
By Proposition 2.1,passing,if necessary,to a subsequence,we may assume thatinE,for someu0∈E.Consequently,Lemma 3.1 and(3.28)imply thatu0is a weak solution of(2.1).
Finally,we show thatu0is nontrivial.By(3.28)–(3.30),we obtain that

Thus,using the boundedness of the sequence(un)and the second relation in(3.28),we find

Let us justify here that Fatou’s lemma can be applied.To this end,we notice that assumptions(H1)–(H4)and(H7)ensure the existence of a(sufficiently large)constantc0>0 such that

By Remark 2.5,it is known thatEis continuously embedded inApplying[6,Proposition 3.4],it follows thatEis compactly embedded inbecauseConsequently,up to a subsequence,we may suppose thatinand a.e.in RN,and there is a functionh∈Lτ+p(RN)such thatfor almost allx∈RN.Therefore



Taking into account thatc≤J(u0)andc>0,we conclude thatand the proof is complete.
First of all,we recall a minimax-type lemma which will be used in the proof of Theorem 2.2.
Lemma 3.4(see[16,Lemma 5.1])Let E be a real Banach space,let a functionbe of class C1,and let two positive numbers ρ<r be such that the following condition is ful filled

Denoting

with

then there exists a sequence(un)⊂E×Rsuch that

We are now in the position to prove Theorem 2.2.
Proof of Theorem 2.2Let us start by choosing positive numbersρ<rand a functionβ∈C1(R)such that



SinceEis a re flexive Banach space,andit is easily seen thatand its partial gradients have the expressions

It follows from(3.48),(3.52)and the first relation in(2.2)that

Moreover,from(3.52),(2.3)and(3.49),we obtain

Therefore,applying Lemma 3.4 we obtain a sequencesuch that

Taking into account the relations(3.52)–(3.54),these convergences imply

By(2.3)and(3.58),we see that

Then using(3.50),we deduce that the sequence(tn)is bounded in R.Thus there ist∈R such that along a relabeled subsequence we may suppose

Next,we show that

Indeed,in order to prove the above relation,we first consider the caset/=0.Then fornsufficiently large,writing(3.60)in the form

and since(tn)is bounded away from zero,it results that(vn)is bounded.
Now assume thatThen(3.48)and(3.60)ensure thatIn view of relation(3.62),we have

It turns out from(3.58)that

On the other hand,fromwe deduce

Using(3.62),we obtain

Combining this fact with(3.59),we infer that

By(3.65),(3.67)and(2.4),we obtain

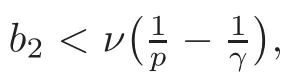
Because(vn)is bounded inE(a re flexive Banach space),we know that there is au∈Esuch that along a relabeled subsequence,one hasinE.According to(3.59),we have

So we obtain

where

Passing eventually to a subsequence,from(3.63)we may assume that there existsand

Lettingin(3.69)–(3.70),and using(2.5)and(3.62),we obtain

with

So from(3.72)–(3.73),we obtain

In addition,from(3.60),(3.62)and the de finition ofθ,we obtain the equality

This implies that

Notice thatIndeed,ifthen(3.73)yields thatis an eigenvalue of(2.6),which contradicts(2.7).Further,we observe from(3.71),in conjunction with the assumptionin(2.2)and the relation(3.72),thatSince,we deduce from(3.75)and(3.51)thatKnowing by(3.51)thatit follows from(3.74)that the inequalitycan be sharpened to

Thus(3.73)and(3.76)imply

Forq=2,from(3.77)we obtain

Forq>2,the relations(3.71)and(3.77)involve(2.8),that is,

and the proof is complete.
[1]Brezis,H.and Marcus,M.,Hardy’s inequalities revisited,Ann.Scuola Norm.Sup.Pisa Cl.Sci.,(4),25(1–2),1997,217–237.
[2]Brezis,H.and Nirenberg,L.,Remarks on finding critical points,Comm.Pure Appl.Math.,44(8–9)1991,939–963.
[3]Brezis,H.and Vázquez,J.L.,Blow-up solutions of some nonlinear elliptic problems,Rev.Mat.Univ.Complut.Madrid,10(2),1997,443–469.
[4]Caffarelli,L.,Kohn,R.and Nirenberg,L.,First order interpolation inequalities with weights,Compositio Math.,53(3),1984,259–275.
[5]Caldiroli,P.and Musina,R.,On the existence of extremal functions for a weighted Sobolev embedding with critical exponent,Calc.Var.Partial Differential Equations,8(4),1999,365–387.
[6]Caldiroli,P.and Musina,M.,On a variational degenerate elliptic problem,NoDEA Nonlinear Differential Equations Appl.,7(2),2000,187–199.
[7]Catrina,F.and Wang,Z.Q.,On the Caffarelli-Kohn-Nirenberg inequalities:sharp constants,existence(and nonexistence),and symmetry of extremal functions,Comm.Pure Appl.Math.,54(2),2001,229–258.
[8]Ciarlet,P.G.,Linear and Nonlinear Functional Analysis with Applications,Society for Industrial and Applied Mathematics(SIAM),Philadelphia,PA,2013.
[9]Dautray,R.and Lions,J.L.,Mathematical Analysis and Numerical Methods for Science and Technology,Vol.1,Physical Origins and Classical Methods,Springer-Verlag,Berlin,1990.
[10]Davies,E.B.,A review of Hardy inequalities,The Maz’ya Anniversary Collection,2,(Rostock,1998),Oper.Theory Adv.Appl.,110,Birkhäuser,Basel,1999,55–67.
[11]Hardy,G.H.,Note on a theorem of Hilbert,Math.Z.,6,1920,314–317.
[12]Kawohl,B.,On a family torsional creep problems,J.Reine Angew.Math.,410,1990,1–22.
[13]Kohn,R.and Nirenberg,L.,Degenerate elliptic-parabolic equations of second order,Comm.Pure Appl.Math.,20,1967,797–872.
[14]Motreanu,D.,A saddle point approach to nonlinear eigenvalue problems,Math.Slovaca,47(4),1997,463–477.
[15]Motreanu,D.and R˘adulescu,V.,Variational and Non-variational Methods in Nonlinear Analysis and Boundary Value Problems,Nonconvex Optimization and Its Applications,67,Kluwer Academic,Dordrecht,2003.
[16]Motreanu,D.and R˘adulescu,V.,Eigenvalue problems for degenerate nonlinear elliptic equations in anisotropic media,Boundary Value Problems,2,2005,107–127.
[17]Oh,Y.G.,Existence of semiclassical bound states of nonlinear Schrödinger equations with potentials of the class(Va),Comm.Partial Differential Equations,13(12),1988,1499–1519.
[18]Pélissier,M.C.and Reynaud,M.L.,Etude d’un modèle mathématique d’écoulement de glacier,C.R.Acad.Sci.Paris Sér.I Math.,279,1974,531–534.
[19]Showalter,R.E.and Walkington,N.J.,Diffusion of fluid in a fissured medium with microstructure,SIAM J.Math.Anal.,22,1991,1702–1722.
[20]Stredulinsky,E.W.,Weighted Inequalities and Degenerate Elliptic Partial Differential Equations,Lecture Notes in Mathematics,1074,Springer-Verlag,Berlin,1984.
[21]Vazquez,J.L.and Zuazua,E.,The Hardy inequality and the asymptotic behavior of the heat equation with an inverse-square potential,J.Funct.Anal.,173(1),2000,103–153.
[22]Wang,Z.Q.and Willem,M.,Singular minimization problems,J.Differential Equations,161(2),2000,307–320.
 Chinese Annals of Mathematics,Series B2016年1期
Chinese Annals of Mathematics,Series B2016年1期
- Chinese Annals of Mathematics,Series B的其它文章
- Solution of Center-Focus Problem for a Class of Cubic Systems∗
- Kinematic Formulas of Total Mean Curvatures for Hypersurfaces∗
- Constructing Invariant Tori for the Spatial Hill Lunar Problem
- The Pointwise Estimates of Solutions to the Cauchy Problem of a Chemotaxis Model∗
- Characterization of Groups L2(q)by NSE Where q∈ {17,27,29}∗
- A Note on Model(Co)slice Categories∗
