Kinematic Formulas of Total Mean Curvatures for Hypersurfaces∗
Ming LI Jiazu ZHOU
1 Introduction
The kinematic formulas are the most beautiful and also useful formulas in integral geometry.At the beginning of his classical paper[4]Chern said:“One of the basic problems in integral geometry is to find explicit formulas for the integrals of geometric quantities over the kinematic density in terms of known integral invariants.”
For instance,Chern proved in[3]the fundamental kinematic formula in then-dimensional Euclidean space En.LetD0andD1be two domains with smooth boundaries∂D0and∂D1,respectively,in En.If we denote byGthe group of rigid motions of Enwith density dg,and byOn−1the volume of the unit sphereSn−1in En,then the fundamental kinematic formula is

whereχ(·)denotes the Euler characteristic,σ(·)the volume andtheithtotal mean curvature.
In[4],Chern gave the integral formulas of the quantities which appear in Weyl’s formula for the volume of tubes.LetM0andM1be two closed smooth submanifolds of dimensionpandqrespectively in En,and then

where the quantitiesμeappear in Weyl’s formula for the volume of tubes(see[14]),0≤e≤p+q−nandeis even.The coefficientsciare constants depending onn,p,qande.
These formulas can also be found in books[11–12].
In his paper[18],Zhou obtained the kinematic formulas for mean curvature power integrals in then-dimensional Euclidean space,which are the generalization of the formulas of the 3-dimensional case in[1,16]and are of the extrinsic type.LetSi(i=0,1)be two closed smooth hypersurfaces in En.Denote byHthe mean curvature ofandThen(see[18])

wherecpqklnare constants depending on the indices,is a kind of total curvature ofThis is a remarkable work in which the moving frame method is effectively used and a successful application of the kinematic formulas is given.
The novel approach to study the containment problem and geometric inequalities by using kinematic formulas has been systematically developed.For the recent developments,interested readers can refer to[8–10,15–23].We also recommend the books[11–12]for the classical results of integral geometry and its applications.
In fact,integral geometry can be set up within the framework of the theory of homogeneous spaces.
LetGbe a unimodular Lie group with kinematic density dgandHa closed subgroup ofG.LetMandNbe two compact submanifolds in the homogeneous spaceG/H,Mfixed andgNthe image ofNunder a motiong∈G.LetI(M∩gN)denote some kind of global geometric invariants ofM∩gNwhich may be volume,curvature integral,etc.Then the goal of the kinematic formulas related to the invariantI(M∩gN)is to evaluate the following integral

by the known integral invariants ofMandN.
Howard proved in[7]a theorem of kinematic formulas in arbitrary homogeneous spaces.It indicates the computability of kinematic formulas with which the related invariants are of the following type

wherehis the second fundamental form ofinG/H,Pis an invariant polynomial in the components ofhwith value,anddσ(x)is the volume element.
This theorem is general and implicit.However,it still requires concrete calculation to obtain explicit formulas,particularly when the kinematic formula is of the extrinsic type.
We prefer the formulas in the Euclidean case.First,because they are important from the point of view of their applications,and second,because they lead to more computable results.
In this paper,we give another kind of explicit kinematic formulas about two closed orientable hypersurfaces in En,n≥3.The manifolds that appear are assumed to be smooth.
We will denote the group of rigid motions of EnbyG.The isotropic subgroup ofGis denoted byG0.IndeedG0is the special orthogonal groupSO(n).The groupsGandG0are unimodular with canonical densities dgand dg0respectively.Let dσbe the Lebesgue measure of En,and then we haveMoreover,the total volume ofG0denoted byJnis finite and given by

whereOi−1is the volume of thei−1 dimensional unit sphere in Eiwith the value

Our motivation comes from the following formulas in[6,12–13].For example,letMbe a closed hypersurface in En,and then

In this formula,the integerisatis fies 0≤i≤n−2,Lis a random oriented hyperplane,and dLis the canonical invariant measure atdenotes themean curvature integral ofwhich is considered as a hypersurface inL.Similarly,for the sake of simplicity.
Taking an arbitrary orientable closed hypersurface in place ofL,we obtain the following kinematic formula.It is not of Howard’s type.
Theorem 1.1Let S0and S1be two closed oriented hypersurfaces in the n-dimensional Euclidean spaceEn.For any integer i satisfying0≤i≤n−2,we have an asymmetric kinematic formula

where the coefficientsc(p,i,n)depend only on p,i and n with value

Note that the formula(1.3)can be viewed as a limiting case of(1.4).
Remark 1.1By direct observation,ifiis even,then(1.4)is just a special case of(1.1)for the hypersurfaces.
But the situation is different ifiis odd.The simplest case isi=1.Sinceis actually the volumeσ(·),we have the following result.
Corollary 1.1Let S0and S1be two closed oriented hypersurfaces in the n-dimensional Euclidean spaceEn.Then

More speci fically,foris the total geodesic curvature of the curve,denoted asThen the above formula is

The formula(1.5)gives exactly an integral representation of the total mean curvature based on any given closed hypersurface.
2 Preliminaries
In the papers[3–4],Chern associated each given Riemannian manifold certain fiber bundle with canonical densities.These concepts and the moving frame method have been proved to be effective in integral geometry.We would like to follow this way in this paper.
We agree in this section on the following indix ranges:

2.1 Fundamental equations of submanifolds
LetMbe anm-dimensional submanifold in an orientedn-dimensional Riemannian manifoldNwith Riemannian metricandthe identity map.
First of all,we mention the local structure ofM(see[5]).LocallyMcan be attached to a Darboux framee1,···,em,em+1,···,en,which is a smooth orthonormal frame field and satis fies thate1,···,emis tangent toM.In the rest of this article,when we mention frames tangent to an oriented manifold,it is always assumed that the orientation of the frames has been chosen to be compatible with the orientation of the given manifold.So here the orientation ofe1,···,emande1,···,em,em+1,···,enis the same as that ofMandNrespectively.
Letrespectively be the canonical forms and the Levi-Civita connection forms on the orthogonal groupSO(n)principle bundleSO(N)under arbitrary extension of the given Darboux frame.These forms can be pulled back onMby the Darboux frame.The images are still denoted by
Let∇be the Levi-Civita connection on the tangent bundleTN,and then we have

and

From the above equation,we obtain

The quantitiesare the components of the second fundamental form ofM.
We review the de finition of the mean curvature integrals of a hypersurfaces as follows.Letm=n−1,and thenMis an oriented hypersurface inN,which has a chosen orientation.Theithmean curvature is related to the following characteristic polynomial oforfor simplicity in the hypersurface cases.Let

and then theithmean curvature is de fined as

and theithtotal mean curvature,if it exists,is denoted by

In this paper,we writeinstead ofto emphasize that the calculation is done inN,sinceMmay be simultaneously a submanifold of other ambient spaces.Notationis used for the same purpose.
2.2 Associated fiber bundles of M
For a fixed nonnegative integerk,we de fine a spaceEkassociated withMby the set

is a fiber bundle with the base spaceMand the fiberEkis called the tangentk-bundle ofMhere.In fact,Ekis an orientable differentiable manifold of dimensionAt any point where(x;e1,···,ek)∈Ek,one extends(x;e1,···,ek)to be a Darboux framee1,···,enbesidex,and then de fines the following form:

whereis the volume element ofM,and the restriction ofon the fibers is indeed the density ofSO(m)/SO(m−k).It is proved in[3],that Θ is independent of the choice of extension and is well de fined onEk.It gives rise to a density ofEk.
3 Proof of Theorem 1.1
LetS0andS1be two closed oriented hypersurfaces in then-dimensional Euclidean space En.The tangent(n−2)-bundles ofS0andS1are denoted byEn−2,0andEn−2,1,respectively.
For eachg∈Gsuch thatis the tangent(n−2)-bundle ofwith density Φg.Then Φg∧dgis a density of the setD={(X,Y,g)∈
For any point(x;e1,···,en−2)ofwe complement it into an orthonormal framesuch thatis orthogonal toS0and also into an orthonormal framesuch thatis orthogonal togS1.Letθ∈(0,π)be the angle betweenand,and then the following differential formula(see[3–4,11–12])is well known for the density ofD:

where Θ0and Θ1are the densities ofEn−2,0andEn−2,1,respectively.Indeed the right side of(3.1)is a density of
Observe that the subset ofDisfor fixedg∈G,and the left side of(1.4)writes as

By(3.1),we see that the above integration is

We turn our attention to the computation of.The problem is to givea representation by the curvatures ofS0andgS1atwhen the motiongis fixed.
From now on,the indexesi,j,kare agreed to range from 1 to(n−2),andA,Bfrom 1 to(n−1).
The induced Levi-Civita connection ofgS1is actuallydof Enprojected on the tangent space ofgS1.Hence the curvature ofwith respect togS1is given by

We here denote bythe dual basis with respect to the framee1,···,en−2,and byω1,···,ωnwith respect toe1,···,en.
From the relation

can be represented as

Then

If we attach an orthonormal frame fieldv1,···,vn−1onS0andongS1nearx,the correspondent dual orthonormal frame fields areη1,···,ηn−1andη′1,···,η′n−1,and then there exist orthogonal matricesandsuch that

Now we assume thatandare the principle tangent vectors ofS0andgS1,respectively,and then

whereκAandare the principle curvatures ofS0andgS1atx,respectively.
With the aid of these notions,we reformulate the right side of(3.3)into

The reason of the last equality is that we calculate inandωn−1=ω′n−1=0.
By the linear independence ofωi,we represent the curvature ofas

Following Chern[3],we are going to expand the determinant of(hij)as the polynomial ofandBy the multilinearity of the determinant,one has

whereis the sum of some(n−2)×(n−2)-determinants,and one term in the summation is

while others can be obtained by permuting some upscriptA’s with some upscriptB’s in(3.4),but preserving the orders ofA1A2···AqandB1B2···Bpto themselves.If some elements ofA1A2···AqorB1B2···Bpappear twice,then clearly
By this observation,one has

where

withσandτrunning through the permutation groups of orderqandp,respectively.
The equations(3.5)then imply that

where the summation indexsruns from 1 toq,andtfrom 1 top.So we obtain the following formula about det(hij):

where

and
More generally,we will discuss the coefficients of the characteristic polynomial

It is clear that det(hij)=ψn−2.By a result in linear algebra,theithcoefficient is given by

A similar discussion about det(hij)gives that

where

One notes that the coefficientsatxare only dependent on the relative position ofS0andS1,and they are invariant if the framee1,···,en−2is acted by an element ofO(n−2).
Then the integration(3.2)continues as follows:

The last equality deserves more explanations.Now we are going to discuss the integral ofoverBy fiber integration,we have

One notes that the densitiesandareSO(n−1)invariant respectively.One also remembers thatandare coefficients ofeiandwith respect tovAandrespectively.For any combinations 1≤j1<···<ji≤n−2,there exists a rotation inSO(n−1)by whiche1,···,eiis rotated to the position ofej1,···,eji.So the fiber integral is

On the hypersurfaceS0,for two sets of different indexesA1,···,Aqandthere exists a rotationginSO(n−1),such thatThe same statement is also valid forS1.Let

and then Ω(p,i,n)are independent of the choices ofA1,···,Ai−pandB1,···,Bp.
If we denote theithelementary symmetric polynomial of the elementsas{aA1···aAi},then the integration ofonis
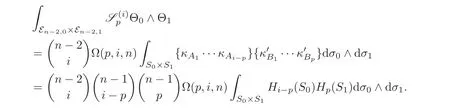
Instead of direct calculation of Ω(p,i,n),we prefer to determine the universal constants c(p,i,n)by takingS0andS1to be hyperspheres,and then evaluate Ω(p,i,n).
The constants will be determined in the last section.We complete the proof of Theorem 1.1.
4 Determination of the Constants
Letandbe hyperspheres in Enof radii 1 andR(0<R<1)respectively.LetS0be centered at the origin pointO.For a fixed motiong,letybe the distance fromOto the center of
Whenwhich is equivalent tois a hyperspherein a hyperplane of radius

It can be proved that
So we obtain


In this speci fic case,the left side of(1.4)reads

By the polar decomposition of Lebesgue measure dσand using(4.1),the above integration is

Puttingwe reformulate the integration as

By the formula(1.2),the kinematic formula for the hyperspheresS0=Sn−1(1)andS1=Sn−1(R)is proved to be

So the universal coefficients in(1.4)are given by

As a consequence,one has

AcknowledgementsThe first author would like to thank Prof.Huitao Feng for his consistent support and encouragement.The authors would like to thank the referees for their helpful comments and suggestions.
[1]Chen,C.-S.,On the kinematic formula of square of mean curvature,Indiana Univ.Math.,22,1972–1973,1163–1169.
[2]Chern,S.S.,On integral geometry in Klein spaces,Ann.of Math.,43(2),1942,178–189.
[3]Chern,S.S.,On the kinematic formula in the Euclidean space ofndimensions,Amer.J.Math.,74,1952,227–236.
[4]Chern,S.S.,On the kinematic formula in integral geometry,J.Math.and Mech.,16(1),1966,101–118.
[5]Chern,S.S.,Chen,W.and Lam,K.S.,Lectures on Differential Geometry,Series on Univ.Math.,Vol.1,World Scienti fic,Singapore,1999.
[6]Gallego,E.,Naveira,A.M.and Solanes,G.,Horospheres and convex bodies inn-dimensional hyperbolic space,Geom.Dedicata,103,2004,103–114.
[7]Howard,R.,The kinematic formula in Riemannian homogeneous spaces,Mem.Amer.Math.Soc.,509,1993,1–69.
[8]Jiang,D.,Zhou,J.and Chen,F.,A kinematic formula for integral invariant of degree 4 in real space form,Acta Math.Sin.(Engl.Ser.),30(8),2014,1465–1476.
[9]Klain,D.,Bonnesen-type inequalities for surfaces of constant curvature,Adv.Appl.Math.,39,2007,143–154.
[10]Li,M.and Zhou,J.,An isoperimetric de ficit upper bound of the convex domain in a surface of constant curvature,Sci.China Math.,53(8),2010,1941–1946.
[11]Ren,D.,Topics in Integral Geometry,World Scienti fic,Singapore,1994.
[12]Santaló,L.A.,Integral Geometry and Geometric Probability,Cambridge University Press,Cambridge,2004.
[13]Solanes,G.,Integral geometry of equidistants in hyperbolic spaces,Israel J.Math.,145,2005,271–284.
[14]Weyl,H.,On the volume of tubes,Amer.J.Math.,61,1939,461–472.
[15]Xia,Y.,Xu,W.,Zhou,J.and Zhu,B.,Reverse Bonnesen style inequalities in a surface X2εof constant curvature,Sci.China Math.,56(6),2013,1145–1154.
[16]Zhou,J.,A kinematic formula and analogues of Hadwiger’s theorem in space,Contemp.Math.,140,1992,159–167.
[17]Zhou,J.,The sufficient condition for a convex body to enclose another in R4,Proc.Amer.Math.Soc.,121(3),1994,907–913.
[18]Zhou,J.,Kinematic formulas for mean curvature powers of hypersurfaces and Hadwiger’s theorem in R2n,Trans.Amer.,Math.,Soc.,345(1),1994,243–262.
[19]Zhou,J.,On the Willmore de ficit of convex surfaces,Tomography,Impedance Imaging,and Integral Geometry,Lectures in Appl.Math.,Vol.30,1994,279–287.
[20]Zhou,J.,When can one domain enclose another in R3?J.Austral.Math.Soc.(Ser.A),59(2),1995,266–272.
[21]Zhou,J.,Sufficient conditions for one domain to contain another in a space of constant curvature,Proc.Amer.Math.Soc.,126(9),1998,2797–2803.
[22]Zhou,J.,The Willmore functional and the containment problem in R4,Sci.China Ser.A,50(3),2007,325–333.
[23]Zhou,J.,On Willmore inequality for submanifolds,Canad.Math.Bull.,50(3),2007,474–480.
 Chinese Annals of Mathematics,Series B2016年1期
Chinese Annals of Mathematics,Series B2016年1期
- Chinese Annals of Mathematics,Series B的其它文章
- Solution of Center-Focus Problem for a Class of Cubic Systems∗
- Constructing Invariant Tori for the Spatial Hill Lunar Problem
- The Pointwise Estimates of Solutions to the Cauchy Problem of a Chemotaxis Model∗
- Characterization of Groups L2(q)by NSE Where q∈ {17,27,29}∗
- A Note on Model(Co)slice Categories∗
- Eventual Positivity of Hermitian Polynomials and Integral Operators
