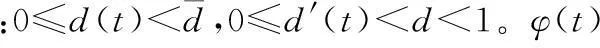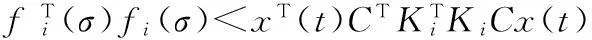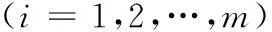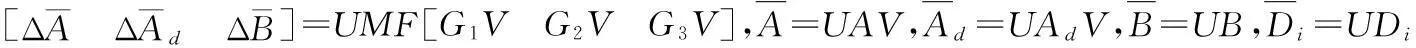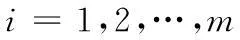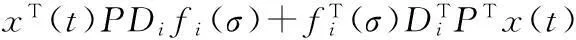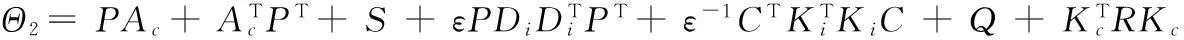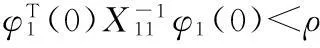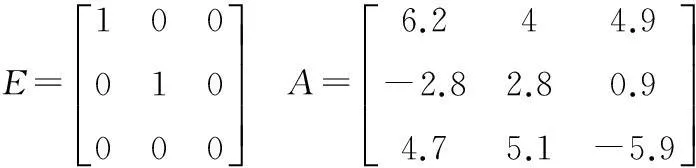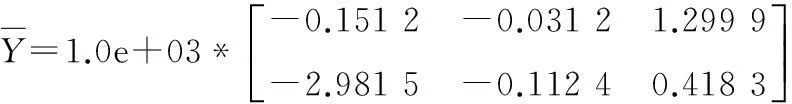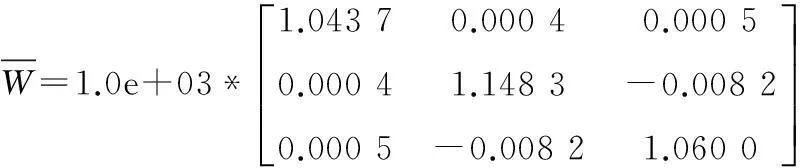非线性奇异时滞系统的鲁棒同时保性能优化控制

李瑞杰，包俊东

(内蒙古师范大学 数学科学学院，呼和浩特　010022)



非线性奇异时滞系统的鲁棒同时保性能优化控制

李瑞杰，包俊东

(内蒙古师范大学 数学科学学院，呼和浩特010022)

摘要：针对一组非线性奇异时滞系统的鲁棒同时保性能控制问题进行研究，用范数有界的不确定参数的微分方程组描述所考虑的系统；基于Lyapunov-Krasovskii泛函和线性矩阵不等式方法给出存在同时保性能控制器的充分条件；对具有线性矩阵不等式约束的凸优化问题求解,进而明确给出使得性能指标函数上界达到最优值控制器的表达式；该控制器的设计方法不仅使得奇异时滞闭环系统组正则、无脉冲、同时鲁棒稳定，而且性能函数上界最优；最后，给出算例验证该方法的有效性。

关键词：非线性奇异系统；时滞；不确定；同时保性能控制；线性矩阵不等式

奇异系统是比较广泛的动态系统，与实际生产生活联系密切，因此奇异系统控制问题引起学者的研究兴趣。由于时滞现象以及外部扰动的出现影响了系统的稳定性，越来越多学者研究满足系统稳定各种性能的控制器。如徐胜元等[1]对范数有界的不确定项利用鲁棒镇定控制得到状态反馈控制器设计方法，后来鲁仁全,苏宏业，俞立[2-4]提出鲁棒控制、最优保性能控制等。然而不足之处在于这些控制都是针对时滞奇异系统的单一目标进行设计，实际系统中常常需要满足实际需要的更好性能。控制系统多目标设计受到人们广泛的重视，文献[5]针对线性奇异时滞系统提出鲁棒H∞控制，这种控制既保证了系统的鲁棒稳定又使得外部扰动控制在γ衰减度内。文献[6]对线性系统提出鲁棒H∞最优保性能控制。

非线性奇异系统相对于线性更能贴切描述实际工程中复杂系统。因此，学者对非线性时滞奇异系统的控制问题给予高度关注。非线性时滞奇异系统在鲁棒控制、H∞控制、保性能控制问题上取得颇丰研究成果。比如徐胜元，杨成梧[7]研究了不确定非线性广义系统的鲁棒控制。王岩青，姜长生在文献[8]对状态为非线性的不确定线性变时滞系统的状态控制器设计进行研究。文献[9]中介绍当状态和输入均有时滞出现时非线性不确定广义系统的保性能控制器设计。保性能控制也可以应用在非线性时滞广义切换系统中[10]。最近几年，陆续出现多种控制结合的方法满足非线性闭环时滞奇异系统所期望的不同性能。文献[11]利用鲁棒控制、H∞控制与保性能控制研究非线性奇异系统。值得一提的是这些研究成果都没有提到所设计控制器是否同时控制多个非线性时滞奇异系统。

同时镇定问题首先由SAEKS等[12]源于实际工程中多模型特征系统稳定的需要首先提出。在国内，曹永岩，孙优贤[13]由状态空间的互质分解提出同时镇定问题研究。2011年关强，何冠男等[14]在回顾前人同时镇定方法后，对“比利时巧克力问题”，“香槟问题”等进一步探讨分析同时镇定问题。至今，同时镇定问题仍是学者关注的热点领域。王德进[15]研究了线性不确定系统族的同时保代价控制，并没有涉及到非线性。鲁仁全等[16]研究了非线性时滞奇异Lurie系统的最优控制问题，基于线性矩阵不等式给出系统存在保代价控制器的充分条件并利用优化问题求出保代价函数的最小值。不足之处在于并没有考虑多个非线性时滞奇异系统的最优控制问题。

本文创新之处在于所设计鲁棒保性能控制器不再局限于单一系统而是能同时适用于多个非线性不确定时滞奇异系统，或者说设计出的控制器可以使多个非线性时滞奇异系统共用。本文针对一组非线性奇异时滞系统的鲁棒同时保性能控制问题展开讨论。所考虑系统中非线性项位于有限的霍尔维茨角域且不确定的参数满足范数有界。在状态变时滞有界的情况下，给出同时保性能控制器以及保性能函数的定义，基于Lyapunov-Krasovskii泛函和线性矩阵不等式方法给出存在同时保性能控制器的充分条件。进而用线性矩阵不等式形式给出使系统鲁棒稳定且使得最优保性能指标函数有最小上界控制器的充分条件。所得结果不仅保证闭环系统组鲁棒渐近稳定，而且使得性能指标函数上界达到最小值，即实现系统的优化控制。最后，用算例结合matlab 工具箱求得可行解来说明本文方法的有效性。

1系统描述与预备知识

考虑下面非线性不确定Lurie时滞奇异系统：

(1)

其中x(t)∈Rn为系统状态向量，u(t)∈Rm为系统控制输入，E∈Rn×n是奇异阵，不失一般性，假设rankE=r

(2)

(3)

其中kij>0是标量，注意到由系统描述式(1)和式(3)，式(3)可等价下面的表达式：

非线性时滞系统组式(1)的标称系统可以写成如下形式：

(4)

由于E是奇异阵，不失一般性，可以假设

(5)

其中Ir表示r×r阶的单位阵，对任何形式的E满足rankE=r

(6)

与系统组式(1)相关联的的性能指标函数取为

(7)

其中对称正定矩阵Q，R为加权阵。

本文的目的是讨论非线性不确定时滞Lurie奇异系统的鲁棒同时保性能控制问题，首先给出该问题的定义：

定义1考虑系统组(1)，如果存在状态反馈控制律

(8)

Kc∈Rm×n为状态反馈增益阵和标量J*满足允许的不确定性，使得闭环系统鲁棒稳定且性能函数式(7)闭环值满足J

引理1[17]给定适当维数的矩阵U，V，W，其中W是对称的，则

W+UFV+VTFTUT<0

对所有满足FTF≤I的矩阵F成立，当且仅当存在一个常数ε>0，使得

引理2[18]对于任意矩阵P，R和对称正定矩阵Q，有以下不等式成立：

PTR+RTP≤PTQP+RTQ-1R

引理3[19]奇异系统

Ex′(t)=Ax(t)

的解是正则、无脉冲，当且仅当存在矩阵X满足

XTE=ETX≥0，XTA+ATX<0

引理4[20-21]非线性时滞奇异系统组的标称系统(4)在u(t)=0时是鲁棒稳定的，如果存在正定对称阵N>0，和矩阵L，以及标量ε>0满足

ELT=LET≥0

(9)

证明：由schur补性质及式(9)，容易得到ALT+LAT<0。利用引理3可知矩阵对(E,A)是正则、无脉冲，即标称系统组式(4)是正则、无脉冲。系统组的鲁棒稳定性可由文献[4]中定理1的证明过程推出。

2主要结果

下面给出非线性时滞标称闭环系统存在同时保性能控制器的充分条件以及相关性能函数的上界。

定理1如果存在正定对称矩阵S，可逆阵P，以及正常数ε满足如下的矩阵不等式：

LET=ELT

(10)

(11)

其中Ac=A+BKc，i=1,2,…，m，L=P-1，矩阵P具有形式

(12)

P11∈Rr×r是正定对称阵，P12∈Rr×(n-r)，P22∈R(n-r)×(n-r)是可逆阵。则u(t)=Kcx(t)是标称系统组式(8)的同时保性能控制律，且此时相关的保性能函数有

证明：首先考虑状态反馈控制下，标称系统构成的闭环系统组：

(13)

下证闭环系统式(13)的鲁棒稳定性。

由式(5)和式(12)中矩阵E，P具有的形式可知：

PE=ETPT>0

(14)

在式(14)两边左乘P-1，右乘P-T，由P-1=L，得到式(9)。

取闭环系统式(12)的同时候选的Lyapunov-Krasovskii泛函：

因为矩阵PE和S均为正定对称阵，所以泛函V(x(t))正定。

定义如下辅助函数：

(15)

V(x(t))沿着闭环系统(13)对t求导得：

由引理1和引理2可以得到下面不等式：

(16)

(17)

只有

(18)

(19)

由式(14)和(19)结合定理1可知：非线性时滞奇异闭环系统式(13)鲁棒稳定。

下证性能指标函数有上界：

若Γ<0，即xT(t)Qx(t)+uT(t)Ru(t)<-V′(x(t))成立。

在上式两端对t进行0到∞积分，有：

因闭环系统式(13)鲁棒稳定，则V(x(∞))→0。故

即保性能函数指标有上界。

只需

即

(20)

由schur引理知：式(20)与式(11)等价，定理证毕。

下面给出带有不确定项的非线性时滞系统式(1)闭环系统存在鲁棒同时保性能控制器的充分条件并给出此时相关保性能函数的上界。

定理2如果存在正定对称阵W，可逆矩阵X，矩阵Y以及正常数ε,ε1满足下面矩阵不等式：

(21)

X11∈Rr×r是正定对称阵，X12∈Rr×(n-r)，X22∈R(n-r)×(n-r)是可逆阵。进而若式(21)有一组可行解W，X，Y，ε，ε1，则非线性时滞奇异系统式(1)的闭环系统的同时鲁棒保性能控制器为：u(t)=YX-Tx(t)，且闭环系统保性能函数的上界为

(22)

证明：在定理2中式(11)加入不确定项，并用schur引理有

(23)

利用式(2)中定义的不确定项代入式(23)，得到等价的不等式：

(24)

式(24)由引理1，存在ε1>0可以得到等价的不等式

由schur引理上式等价于

(25)

定理中式(21)提供了一组鲁棒同时保性能控制器的设计参数方法，下面给出通过解决优化问题得到使保代价函数闭环值最小最优同时保性能控制器的设计方法。

定理3考虑非线性不确定时滞奇异系统(1)，如果下面的优化问题：

(26)

证明：由E,P的具体形式可知，系统的保性能函数的上界式(21)等价于

(27)

Trace(VVTW-1)=Trace(VTW-1V)

因此式(27)可以得到

J*<ρ+Trace(Z)

即对式(26)求最小值也就是对式(22)求最小值上界，证毕。

3仿真算例

考虑非线性不确定时滞奇异系统(1)，取m=2，相关参数如下：

利用Matlab工具箱对定理3中优化问题式(25)求解，结果如下：

ρ=-246.207 2Z=9.583 4

ε=10.315 4ε1=442.822 0

非线性时滞奇异闭环系统式(1)的同时保性能控制律为：

此时得到的保性能函数上界为：J*=-236.623 8，所得保性能控制律不仅保证具有所允许的不确定性的非线性时滞奇异系统组(1)鲁棒渐近稳定，而且确保性能函数的上界最优。

4结论

本文研究了非线性时滞奇异系统的鲁棒同时保性能控制问题。给出同时保性能控制器以及保性能函数的定义，基于Lyapunov-Krasovskii泛函以线性矩阵不等式形式给出同时保性能控制器存在的充分条件，并通过对具有线性矩阵不等式的凸优化问题求解得到保性能函数上界最小值的控制器设计方法，使得闭环系统组鲁棒稳定且性能函数上界最优。利用Matlab工具箱得到可行解，并通过算例验证本文方法的可行性。

参考文献：

[1]XU S Y,DOOREN P V,STEFAN R,et al.Robust stability and stabilization for singular systems with state delay and parameter uncertainty[J].IEEE Transaction on Automatic Control,2002,47(7):1122-1128.

[2]LU R Q,SU H Y,CHU J.A memoryless robust stabilizing controller for a class of uncertain singular time delay systems[J].Int Journal of Systems Science,2004,36(10):973-981.

[3]YU L,XU J M,HAN Q L.Optimal guaranteed cost control of singular systems with Time-delay and parameters uncertain[C]//Proc of American Control Conf,2004(5):4811-4816.

[4]LU R Q,SU H Y,CHU J.RobustH∞control for a class of uncertain Luire singular systems with time-delays[C]//Decision and Control,Proc.42ndIEEE Conf.,2003(6):5585-5590.

[5]JI X F,SU H Y,CHU J.An LMI approach to robustH∞control for uncertain singular time-delay systems[J].Journal of Control Theory andApplication,2006(4):361-366.

[6]XUE A K,WANG J Z,JIANG N,et.alH∞robust optimal guaranteed cost control with disturbance attenuation performance for uncertain systems[C]//WCICA Fifth World Congress,HangZhou,2004(1):525-529.

[7]徐胜元，杨成梧.一类不确定性广义非线性系统的鲁棒控制[J].控制理论与应用，2000，17(4):624-625.

[8]王岩青，姜长生.一类非线性不确定时滞系统的鲁棒H∞控制[J].信息与控制，2005,34(2):147-151.

[9]谢丽萍，金朝永.非线性不确定时滞广义系统的保性能控制[D].广州：广东工业大学，2015.

[10]张立俊.非线性不确定多时滞切换奇异系统的鲁棒H∞保性能控制[J].河北科技大学学报，2015,36(2):150-156.

[11]刘树娜，仇计清.非线性广义系统的鲁棒H∞保性能控制研究[D].石家庄：河北科技大学，2013.

[12]SAEKS R,MURRAY J.Fractional representation,algebraic geometry,and the simultaneous stabilization problem[C].IEEE Trans.Automat.Control,1982,27:895-903.

[13]曹永岩，孙优贤.同时镇定问题研究[J].信息与控制，1998， 27(3)：161-166.

[14]关强，何冠生，王龙，等.线性系统的同时镇定问题[J].控制理论与应用，2011，28(1)：1-10.

[15]王德进.线性不确定系统族同时保代价控制[C]//proceedings of the 25thChinese control conference，Harbin，Heilongjinag，2006，698-700.

[16]LU R Q,SU H Y,WANG J Z,et.al.Robust Optimal Control for a class of Nonlinear Uncertain Singular Systems with Time-delay[C]//proceedings of the 2006 American Control Conference,Minneapolis,Minnesota,USA,2006,5020-5024.

[17]LU R Q,SU H Y,CHU J.A memoryless robust stabilizing controller for a class of uncertain singular time delay systems[J].Int Journal of Systems Science,2004,36(10):973-981.

[18]XIE L,DE SOUZA C E.RobustH∞control for linear time-invariant systems with norm-bounded uncertainty in the input matrix[J].Sys Control Letter,1990,14(5):389-396.

[19]MASUBUCHI I,SUDA N,OHARA A.LMI-Based controller synthesis:a unified formulation solution[C]//Proc American Control Conf,1995:3476-3477.

[20]户永清.基于模糊自适应PID控制的汽油发电机逆变电源设计[J].重庆工商大学学报(自然科学版)，2014，31(7)：50-55.

[21]鲁仁全，苏宏业，薛安克，等.奇异系统的鲁棒控制理论[M].北京：科学出版社，2008.

(责任编辑杨继森)

本文引用格式：李瑞杰，包俊东.非线性奇异时滞系统的鲁棒同时保性能优化控制[J].兵器装备工程学报，2016(4):149-154.

Citation format:LI Rui-jie, BAO Jun-dong.Robust Simultaneous Guaranteed Cost Control for Nonlinear Singular Systems with Time-Delay[J].Journal of Ordnance Equipment Engineering,2016(4):149-154.

Robust Simultaneous Guaranteed Cost Control for Nonlinear Singular Systems with Time-Delay

LI Rui-jie, BAO Jun-dong

(Mathematics Science College, Inner Mongolia Normal University, Hohhot 010022, China)

Abstract:The simultaneous guaranteed cost control problem for a group of nonlinear singular systems with time-delay robust was studied. The systems under consideration were described by differential equations which were with norm-bounded and uncertain parameters. A sufficient condition for the existence of simultaneous guaranteed cost controller was derived by the approach which based on Lyapunov-Krasovskii functional and linear matrix inequality(LMI). A convex optimization problem with LMI constraints was formulated, and controller which minimizes upper bound of cost index function was designed exactly. This design method makes sure that closed-loop of singular systems with time delay is not only regular, impulse free, robust stable but also upper bound of cost index function up to minimum. Finally, a numerical example was provided to demonstrate the availability of the proposed method.

Key words:nonlinear singular systems; time-delay; uncertain; simultaneous guaranteed cost control; linear matrix inequality(LMI)

文章编号：1006-0707(2016)04-0149-06

中图分类号：O231.2

文献标识码：A

doi:10.11809/scbgxb2016.04.036

作者简介：李瑞杰(1990—)，女，硕士研究生，主要从事时滞奇异系统的同时镇定与控制研究。

基金项目：内蒙古师范大学2014年度研究生科研创新基金(CXJJS14054)

收稿日期：2015-10-18；修回日期：2015-11-23

【基础理论与应用研究】