含输入和输出时滞离散时间系统的最优跟踪控制*

张 健，宿 浩，杨 清，杜攀攀，唐功友

(1.中国海洋大学信息科学与工程学院，山东 青岛 266100；2.青岛海西重机有限责任公司，山东 青岛 266520)

严格来讲，在实际应用中各类控制系统的时滞是无法避免的。一般而言，信号或物质传递存在时间延迟的系统都是时滞系统。在一个具体的控制系统中，输入时滞和输出时滞可能是由控制机构、执行机构及测量单元本身的运行方式造成的。对于小时滞系统，人们往往忽略时滞的影响。但对于较大时滞系统或对系统性能要求较高的系统，时滞的影响是不能忽略的。因此如何减小甚至消除时滞的负面影响成为备受关注的问题。文献[1]研究了一类含多输入多输出非线性时滞系统的自适应神经网络控制问题。文献[2]研究了采样数据控制下的时变时滞系统在输入时滞受限条件下的同步问题。文献[3]研究了一类存在输入和跟踪误差限制的非线性时滞系统的自适应跟踪控制问题。文献[4]研究了含有时滞和数据丢包的离散时间神经网络的H∞控制问题。文献[5]为一类存在数据丢失和通讯时滞的网络控制系统提出了一种自启动采样方案。文献[6]针对一类含有多重子网络并且每个子网络都含有传感器、控制器和执行机构的大规模分布式网络控制系统，提出了一种解决时滞问题的方法。文献[7]在解决高速网络下时滞系统的扰动抑制问题时，使用了无时滞转换的方法。

近年来在时滞系统的跟踪控制领域也取得了很多研究成果。为解决不规则海浪冲击下海洋平台的跟踪问题，文献[8]提出了一种离散的含前馈和反馈的最优跟踪控制策略。文献[9]在对于含有时滞的分布式输出反馈自适应神经网络跟踪控制问题的研究中，通过使用状态变换的方法，保证了跟踪性能。文献[10]针对受外部扰动影响的时滞系统，在设计基于观测器的最优跟踪控制器时，使用了逐次逼近的方法。文献[11]在跟踪控制问题的研究中，使用了内模控制的方法来补偿由时滞带来的影响。文献[12]研究了测量时滞对光电跟踪伺服系统的影响，并提出了一种自校对的内模控制律。在时变时滞系统位置跟踪问题的研究中，文献[13]构造了一个基于散射变换的控制器。在线性单输入单输出时滞系统的输出跟踪问题的研究中，文献[14]使用了二阶滑模控制的方法。

本文研究含控制时滞和被控输出时滞的离散时间系统，在受到动态特性已知的外部扰动影响下的最优跟踪控制问题。

1 系统模型

研究含有控制时滞和输出时滞的受扰离散时间系统，其状态空间表达式如下：

x(k+1)=Ax(k)+Bu(k-h1)+Dv(k),y(k)=Cx(k-h2),x(0)=x0,u(k)=0,k=-h-1,-h,-h+1,…,-1。

(1)

式中：x(k)∈Rn为状态向量；u(k)∈Rr为控制向量；v(k)∈Rp为外部扰动向量；y(k)∈Rm为时滞系统的输出向量。A、B、C、D分别为适当维数的常量矩阵；h1为控制时滞；h2为输出时滞；h=h1+h2；x0为初始状态。

外部扰动的离散化模型可由如下外系统描述：

w(k+1)=Gw(k),v(k)=Ew(k)。

(2)

式中：w(k)∈Rq(p≤q)为外系统的状态向量；G,E为适当维数的已知常量矩阵；初始条件w(0)可以是未知的。假设扰动外系统(2)是渐近稳定的，即|λi(G)|<1。

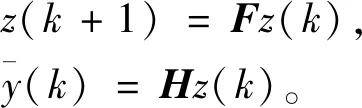
(3)

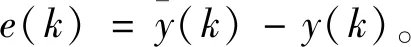
(4)

我们选择如下二次性能指标：

(5)

式中：Q∈Rm×m和R∈Rr×r为预先给定的正定矩阵。

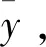
由于系统(1)受到控制时滞、输出时滞和扰动的影响，对于传统的跟踪问题，最优跟踪控制律是不存在的。为设计最优方式下的控制律，我们引入一种变量代换，将含有控制时滞和输出时滞的离散时间系统转化为无时滞系统。从而，将原跟踪问题转化为相对应的无时滞系统的最优跟踪控制问题。

2 控制系统无时滞转化以及性能指标简化

引入如下变量：

(6)

其中

(7)

系统(1)可转化为形式上无时滞的离散时间系统

(8)

根据引入的变量(6)以及无时滞系统(8)，性能指标(5)可转化为如下形式

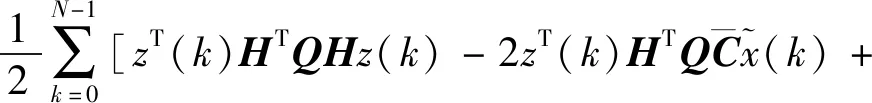
2zT(k)G4w(k)-2wT(k)G3u(k)+

(9)

其中

(10)

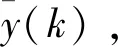
3 最优跟踪控制器设计

定理1 考虑含有控制时滞和输出时滞的离散时间系统(1)、(2)及(3)，满足性能指标(9)的最优跟踪控制律可以表示为

(11)

其中P1为如下Riccati差分方程的半正定解

P1(N)= 0。

(12)

P2为如下矩阵差分方程的解

P2(N)= 0。

(13)

P3为如下矩阵差分方程的解

P3(k)=ATP1(k+1)DE-G5+ATP3(k+1)G+

(14)

其中

(15)

证明 根据化简后的性能指标(9)，构造如下哈密顿函数

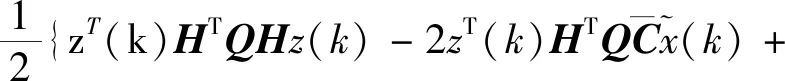
2zT(k)G1u(k)+2zT(k)G4w(k)+

2wT(k)G3u(k)+wT(k)G6w(k)}+

(16)

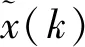
(17)

整理(17)中的第二式可得

(18)

将(18)代入(8)和(17)，我们得到如下TPBV问题

AT)λ(k+1),

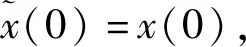
λ(N)=0。

(19)

为解决上述TPBV问题，令

(20)

将(20)代入(18)可以得到(11)。将(11)和(20)代入(19)的第二式可以得到

{ATP1(k+1)DE-G5+ATP3(k+1)G+

(21)

4 控制器的物理可实现设计

注意到，在所提出的控制律(11)中，含有分别由参考输入外系统和扰动外系统的状态向量所组成的前馈项，其在物理上是不可实现的。在本节中，通过构造扰动外系统观测器和参考输入外系统观测器，来实现对扰动外系统和参考输入外系统的观测，从而解决上述物理不可实现问题。

依据扰动外系统模型(2)，构造如下扰动观测器：

(22)

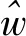
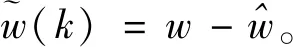
(23)

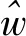
依据参考输入外系统(3)构造如下参考输入外系统观测器：

(24)

通过对w和z的重构，我们可以得到如下形式的最优跟踪控制律

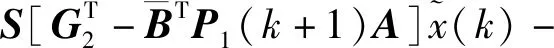
(25)

5 仿真算例

考虑由公式(1)描述的受扰离散时滞系统，其中

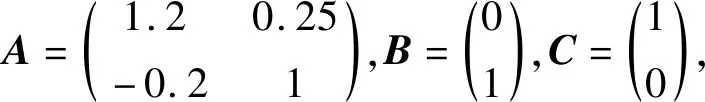
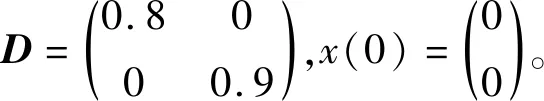
(26)

由公式(2)所描述的外部扰动外系统具体参数如下：

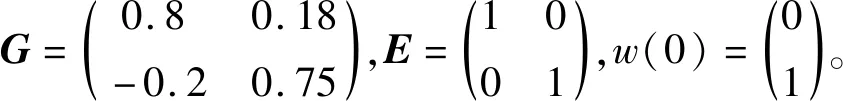
(27)

由公式(3)描述的参考输入外系统具体参数如下：

(28)

公式(5)表示系统的性能指标，其中Q=5,R=1。图1～3分别显示了控制时滞h1=2，输出时滞h2=1时，系统的跟踪轨迹y，跟踪误差e及控制向量u的变化曲线。图4～6分别显示了控制时滞h1=3，输出时滞h2=2时，系统的跟踪轨迹y，跟踪误差e及控制向量u的变化曲线。表1给出了以上2种情况下的性能指标值。

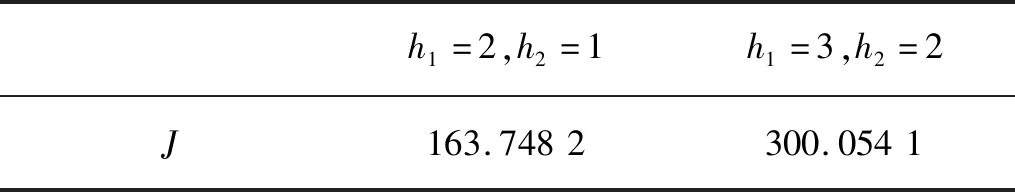
表1 不同时滞下的性能指标Table 1 Performance index under different time delays

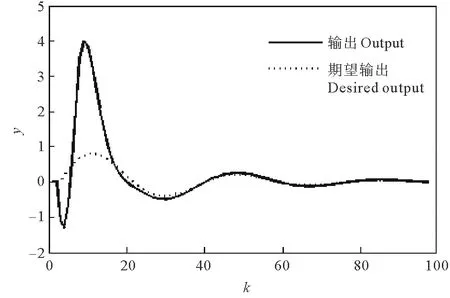
图1 h1=2,h2=1时的参考输入及系统输出Fig.1 Reference input and output (h1=2,h2=1)

由仿真结果可以看出，当外部扰动渐近稳定时，随着时滞的增大，控制质量会逐渐变差，在图上表现为：时滞越大，相同时间点上对应向量的幅值越大。性能指标也会随着时滞的增加而增大。但对于不同的时滞，系统输出总能很好的跟踪参考输入，即跟踪误差能够快速收敛到很小值。所以本文提出的含有控制时滞和输出时滞的离散时间系统最优跟踪控制律的设计方法是有效的。

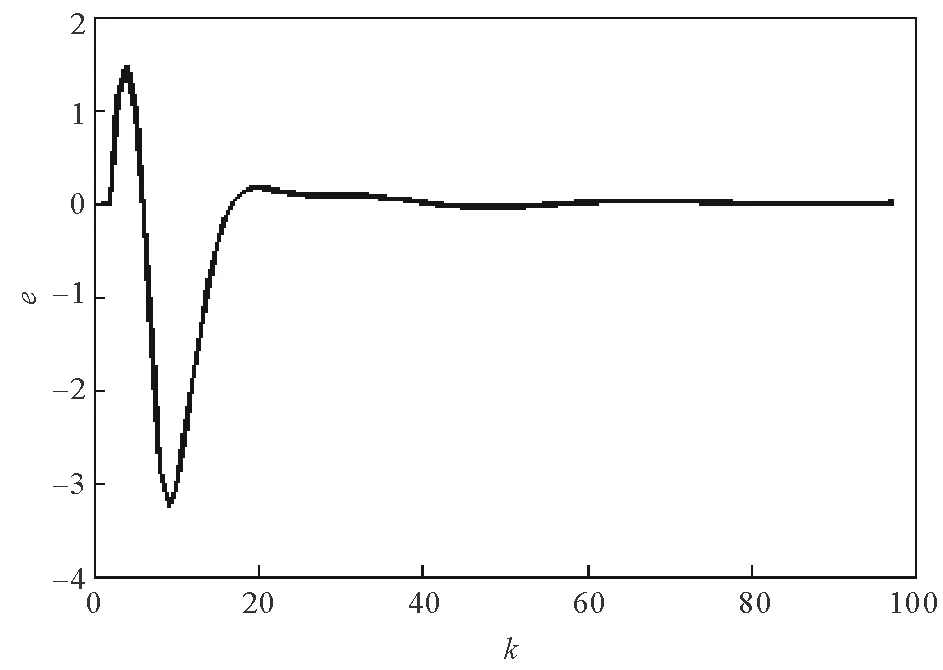
图2 h1=2,h2=1时的跟踪误差Fig.2 Tracking error(h1=2,h2=1)

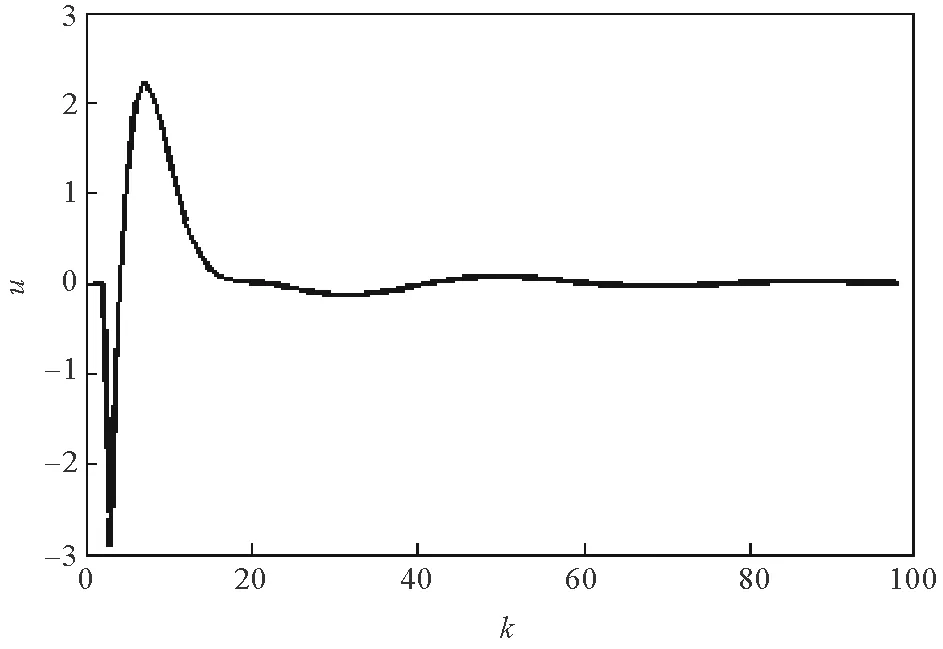
图3 h1=2,h2=1时的控制向量Fig.3 Optimal control law (h1=2,h2=1)

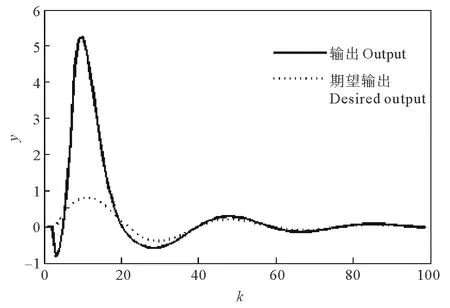
图4 h1=3,h2=2时的参考输入及系统输出Fig.4 Reference input and output (h1=3,h2=2)

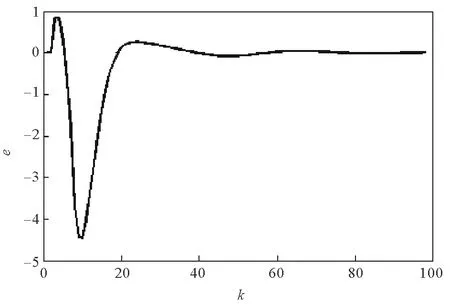
图5 h1=3,h2=2时的跟踪误差Fig.5 Tracking error(h1=3,h2=2)

图6 h1=3,h2=2时的控制向量Fig.6 Optimal control law(h1=3,h2=2)

6 结语

本文研究了在外部扰动的动态特性确定的条件下,含有控制时滞和输出时滞的离散时间系统的最优跟踪控制问题。利用模型转换将原时滞系统转化为形式上的无时滞系统，构造并整理了系统的二次性能指标，设计了系统的最优跟踪控制律。