脉动风速时程数值模拟

程　华，钟华生，周　凌，王　龙

(后勤工程学院　a.军事土木工程系; b.学员旅，重庆　401331)



脉动风速时程数值模拟

程华a，钟华生a，周凌a，王龙b

(后勤工程学院a.军事土木工程系; b.学员旅，重庆401331)

摘要：对高层、高耸和大跨轻柔等风敏感结构而言，风荷载是主要控制荷载，必须考虑风荷载的动力作用。分析了风速时程模拟方法的概况，包括传统的谐波叠加法、线性滤波法，以及近年来发展起来的小波分析、逆傅立叶变换法。采用AR法模拟了某索-桁移动机库的脉动风速时程。总结了各种方法的优缺点，展望了风速时程模拟的前景。

关键词：脉动风速时程；数值模拟；谐波叠加法；线性滤波法；小波分析

随着工程结构日趋多样化、大型化、复杂化，新材料、新工艺、新技术、新形式以及新设计方法的应用，使得结构更加轻柔，结构体型更加复杂，从而使得结构对于风荷载的作用更加敏感，风荷载已成为结构抗风计算、防灾减灾分析的重要设计荷载，结构风振响应研究日益受到重视[1]。目前，虽然在一些较为重要建筑中采用风洞试验或现场实测等手段确定结构承受的风荷载，但这些方法都比较复杂，耗时耗资，不具备通用性。此外，我国地域广阔，地区之间的风速特性也很不相同，已有的强风记录资料有限，不能在结构风振分析中普遍应用。因此，风荷载数值模拟方法在实际工程中得到了广泛采用。

1谐波叠加法

谐波叠加法是基于一系列三角级数求和，采用以离散谱逼近目标随机过程的一种平稳随机过程数值模拟方法。在1954年Rice[2]首先提出谐波叠加法的基本思想，但当时仅适用一维单变量平稳高斯随机过程的模拟。在1972年Shinozuka[3]提出CAWS法和WAWS法，将谐波叠加法发展到模拟多变量、非平稳高斯随机过程。虽然后来Yang等[4]人在谐波叠加法中引入快速傅立叶(FFT)变化技术，大大加速了谐波叠加法的模拟速度，但它的计算量依然较大。采用谐波叠加法模拟风荷载时，需要在每个频率上进行大量运算，并且不能考虑时间相关性。

随机信号可以通过离散Fourier变换分析，分解为一系列具有不同频谱和幅值特性的正弦或其他谐波，谱密度就等于由带宽划分的这些谐波幅值的平方。根据Shinozuka的理论[3]，一组m个s维随机过程xj(t)(j=1,2,…,m)可模拟为：

(1)

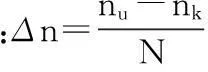
风速时程的互功率谱密度函数矩阵一般形式为：

(2)

(3)

对Sij(n)进行乔里斯基(Cholesky)分解：

(4)

可以得到下三角矩阵元素H(n)，H*(n)Τ是H(n)的转置复共轭矩阵。

θjk(nl)表示Hjk(nl)的相位角：

(5)

为避免模拟结果失真，时间间隔应满足Δt≤π/(2nl)。

当模拟的点大于200时，按常规方法计算最终的风速时程是很耗机时的，建议引入FFT技术[6]，将大大提高计算效率。

取M=2π/(Δt·Δn)为整数，则可将式(1)改写为：

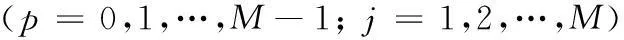
(6)

Gj(p·t)可用傅立叶变换计算：

(7)

其中：

(8)

谐波叠加法简单直观、数学基础严密，很多学者采用经典谐波叠加理论或结合快速傅立叶变换技术模拟脉动风荷载[7-11]，做了大量工作，但很少取得新的突破。李正农等[12]采用非均匀圆频率间隔的方法，改进了以往谐波合成法模拟的周期性缺点，但此种方法是以牺牲效率为代价的。Debasis等[13]在分析总结高斯模型的基础上，提出了一种新的非高斯条件的迭代方法，结合非线性非高斯映射技术，模拟了大跨桥梁的风速时程曲线；并用不同模拟方案的风荷载对大桥进行风振响应分析，与实测数据对比表明，非高斯模拟方案优于高斯模拟方案。Huang等[14]提出了一种全新的针对功率谱密度函数乔里斯基(Cholesky)分解方法，它的关键思想是从复杂EPSD/PSD矩阵分解中分离出各个独立的阶段，最后再以某种特定的方式进行组装，进而大大提高分解效率。

2线性滤波法

线性滤波法则是基于数字滤波技术，将均值为零的白噪声随机序列通过线性滤波器，输出具有指定谱特征的随机过程。线性滤波器包含AR法、MA法和ARMA法，其中AR法被广泛应用于脉动风速时程模拟。

脉动风速时程本质上也是随机时间序列，因此可以采用AR法模拟脉动风的风速时程。m个空间相关脉动风速时程v(X,Y,Z,t)列向量的AR模型可表示为：

(9)

其中：X=[x1,x2,…,xm]Τ、Y=[y1,y2,…,ym]Τ、Z=[z1,z2,…,zm]Τ；(xi,yi,zi)为空间第i点的坐标，i=1,2,…,m；Δt为模拟风速时程的时间步长；p为模型的阶数；φk为AR模型的自回归系数矩阵，为m×m阶矩阵，k=1,2,…,p；N(t)为独立随机过程向量。

为简便起见，以下将v(X,Y,Z,t)简记为v(t)，将式(9)的左右两边同乘vΤ(X,Y,Z,t-jΔt)，并同时取数学期望可得相关函数R(jΔt)与回归系数φk的关系为：

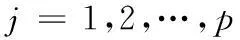
(10)

将式(10)改为矩阵形式为：

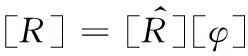
(11)

其中：[R]pm×m=[R(Δt),R(2Δt),…,R(pΔt)]Τ，[φ]pm×m=[φ1,φ2,…,φp]Τ。

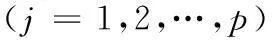
根据随机振动理论，相关函数可由维纳-辛钦公式求出

(12)

式中：n为脉动风速频率；Sij(n)为风速谱函数，可由脉动风速自谱密度函数Sii(n)和相干函数cohij(n)(i=1,2,…,m; j=1,2,…,m)确定

(13)

独立随机过程向量N(t)由下式求解

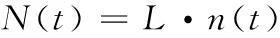
(14)

式中：n(t)=[n1(t),n2(t),…,nm(t)]Τ，ni(t)是零均值、方差为1且彼此相互独立的正态随机过程，i=1,2,…,m；L为m阶下三角矩阵，通过m×m阶协方差矩阵RN的乔里斯基(Cholesky)分解确定

(15)

计算时，假定初始时刻之前的风速为0，即： t≤0时,v(t)=0。最终的m个随机脉动风速时程可表示为

(16)

文献[15-17]中采用基于AR模型的线性滤波法对超高层结构的脉动风速时程进行了数值模拟，验证了其可行性与有效性，且占用内存小、计算速度快。马骏等[18]结合谐波叠加法和自回归法的优点，提出风速时程的高效高精度新型混合法。在保证计算精度下，该方法的模拟效率是谐波叠加法的数十倍；计算精度与自回归方法相比亦显著提高，且易于收敛。曾少青对自回归阶数P=4，5，6，7时的风速谱模拟效果进行对比，发现P=6时模拟谱与目标谱的标准差最小，说明并非阶数越高风速谱模拟精度越高[19]。武秀根等采用AR模型模拟了超限冷却塔的表面风压表明，基于随机脉动风荷载模拟的数值计算方法，特别适用于冷却塔高度超出规范要求的情况下评估冷却塔的风振响应[20]。刘亚庆分析了AR法结合快速傅立叶变换的频率不准确采样误差，由此提出了两种改进方法：一是精确频率小数位数，自振频率的计算结果每多保留一位就会使采样点的个数变为原来的10倍，计算量巨大；二是构造结构相邻两阶自振频率的差值向量，使其模最小，取得了较为显著的效果[21]。

3小波分析

设φ(t)为一平方可积函数，即φ(t)∈L2(R)，L2(R)为平方可积的函数空间，如果其傅立叶变换φ(ω)满足条件[22]

(17)

则称φ(t)为基本小波或小波母函数，而连续小波基函数φα,τ(t) 则通过小波母函数φ(t)的伸缩和平移得到。由同一母函数φ(t)经过伸缩和平移后得到一组函数系列

(18)

式中：α为尺度因子；τ为平移因子。

风工程中使用的信号大都为离散函数，因此对小波加以离散化。在数值计算中最常用的是二进制采样网格。每个网格点对应的尺度为2j，平移量为2jk的小波称为二进小波(Dyadic Wavelet)[23]，即：

(19)

(20)

相应可以将随机信号X(t)表示为一系列离散小波基的叠加[24]

(21)

其中，小波系数Wj,k与尺度系数Uj,k可表示为[25]

(22)

由于自身良好的时频特性，小波分析受到了国内外学者的广泛关注。吴筑海等[26]用分解后的小波系数来描述风速信号在时间与频率两个域上的特性，证实了小波分析在风速时程分析中的稳定性。韩艳等[27]采用正交Mayer小波变换模拟脉动风，发现模拟的脉动风具有一定的间歇性和局部相似性，Yamada等[28]对实测的脉动风进行小波分析，得到了类似结论。Zeldin等[29]采用db3小波，利用AR法来合成每一尺度上的小波系数，而采用多个小波函数来定义多维随机风场模拟。Aksoy等[30]采用Haar小波模拟了1000年风速，并与5种传统的参数模型模拟方法分别进行了比较，发现小波是保留信号相关性的最好方法。

陈艾荣等[31]根据小波的多分辨率分析性质，利用小波重构算法，选取db3小波基，基于线性估计原理，利用逆小波变换反复迭代计算，模拟了苏通桥某点的纵向脉动风速。周岱等[32]采用离散小波变换分解和重构风速时程，并引入最大熵值法减少风速时程分析在时-频域上的信息损失并提高效率。柳杰等[33]采用Haar小波对风速时程进行分解和识别，提高分解后的低频分量，使得风速时程在时-频域上更加逼近目标值。郭立伟等[34]利用db3小波，重构14层，根据AR模型模拟出21条具有空间相关性的脉动风速时程。

李宏男等[35]系统总结了小波分析在结构风工程中的风荷载模拟、风场特性研究、风与风压的相互关系以及模态参数识别中的国内外现状，并对小波变换在结构风工程中的应用前景进行了展望。

4逆傅立叶变换法(IFFT法)

逆傅立叶变换法(IFFT法)[36-37]由D.Cebon[38]首先提出，在国内最早用于铁路不平顺随机过程的模拟[39]。候传亮等[40]针对道路过程，引入道路车辆速度后转换空间频率为时间频率，运用IFFT法和谐波叠加法成功模拟了一种C级道路时间序列。逆傅立叶方法(IFFT)的基本思想是通过时间序列估计功率谱密度的周期图法—Blackman-Tukey法来反推离散后的功率谱密度(PSD)与时间序列的关系：

(23)

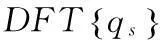
IFFT法为风速时程的数值模拟提供了一种新思路。根据已知的风速功率谱密度，则可以由式(24)反算随机过程的傅立叶频谱值。进而通过对复序列F(k)的IFFT的时序化模型

(24)

5算例分析

以某30 m×40 m索-桁机库(图1)为工程背景，该机库主体结构由10榀索-桁架(图2)组成，两端设有蚌壳式门，骨架采用轻型铝合金型材，屋面敷设M950-2型膜材。采用基于AR模型的线性滤波法，运用Matlab编程模拟脉动风时程，模拟的具体参数见表1所示。

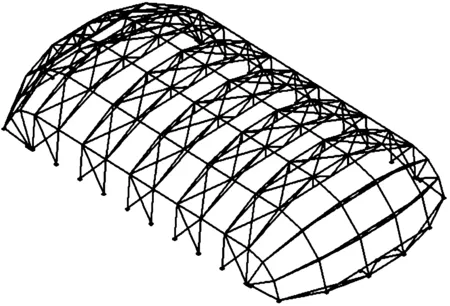
图1　机库结构简图

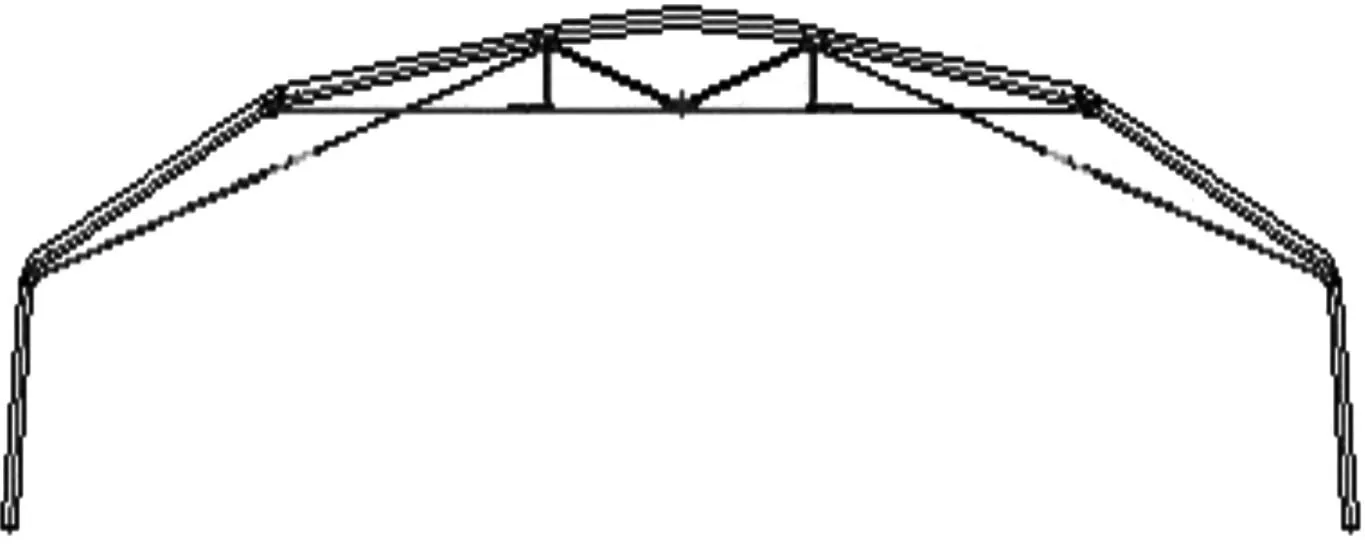
图2　一榀索-桁架简图

图3表示生成的第1点和第10点的脉动风速时程曲线；图4采用双对数坐标，给出了模拟脉动风速自谱功率谱密度与目标谱的对比曲线。可以看出，脉动风速在0上下波动，符合平稳随机过程的特性；模拟风速谱和目标谱吻合较好(尤其在高频阶段)，表明数值模拟的脉动风速时程自相关随机特性满足所需随机特征。

表1　风速时程模拟时的具体参数

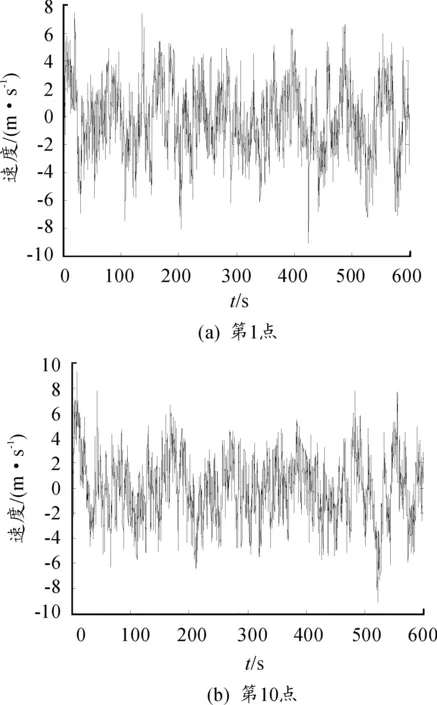
图3　模拟脉动风速时程

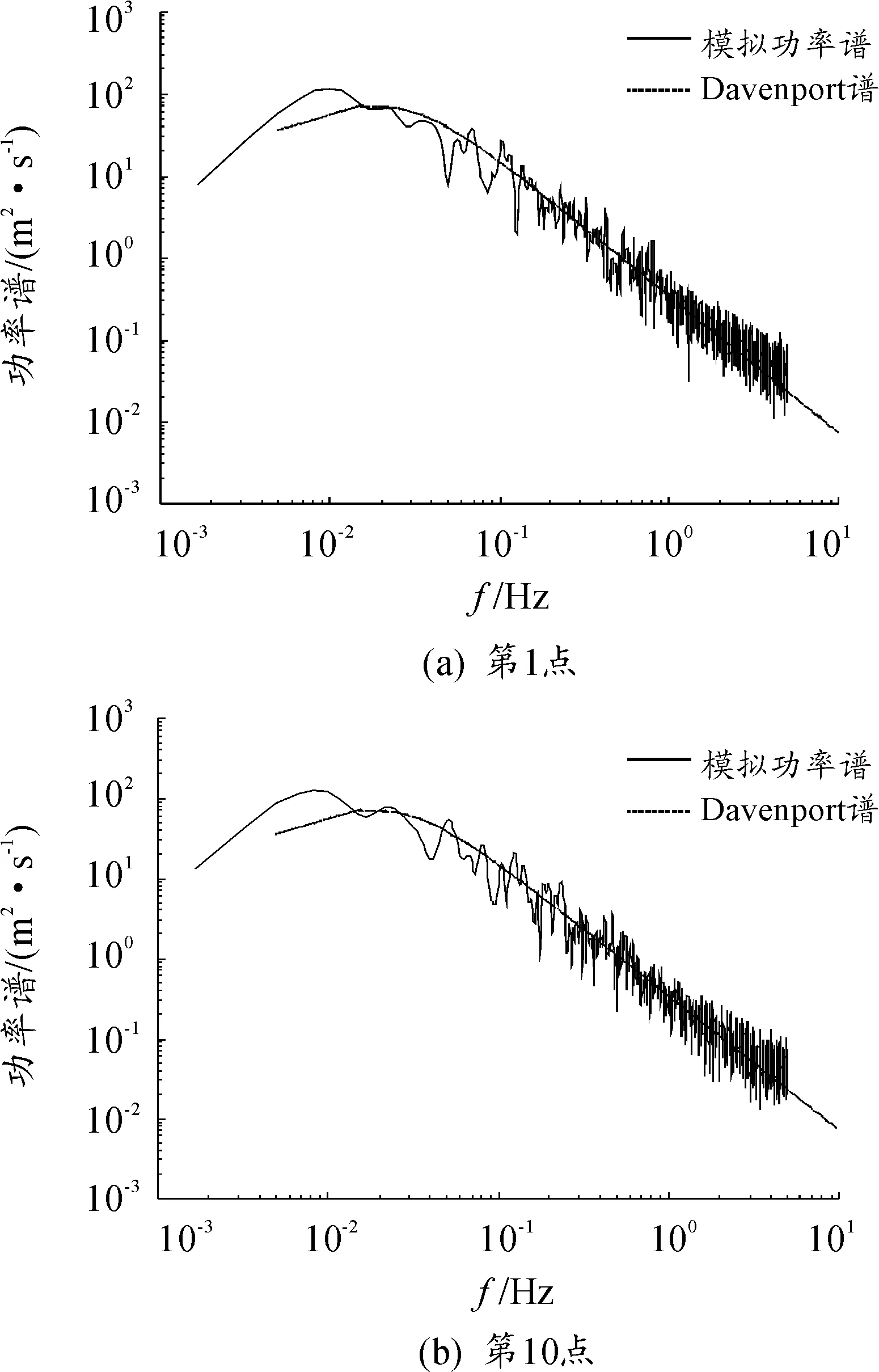
图4　模拟脉动风速功率谱分析

6结束语

本文介绍了模拟脉动风速时程的几种方法，重点介绍了谐波叠加法和基于AR模型的线性滤波法的基本原理，讨论了各种方法的研究近况，并采用AR法模拟了脉动风速时程。

谐波叠加法和线性滤波法都是模拟平稳高斯随机过程的经典方法，能够快速高效地满足工程精度要求，尤其是引入快速傅立叶变换技术后，大大提高了计算效率，在工程界和学术界得到了广泛应用。但谐波叠加法要求谐波频率必须满足均匀分布的条件，且仅适用于线性情况，也不能考虑风速的时间相关性；线性滤波法算法繁琐、精度较差，AR模型定阶还值得深入研究。

小波分析被誉为“数学显微镜”，在时域和频域中有良好的局部化特征，它能够聚焦到风速时程的任意细节并加以分析，快速准确地提取样本的局部谱密度特征，并可用局部能量密度函数表示风频率随时间的变化。作为一种新的模拟工具，小波分析在风速时程的模拟研究中具有广阔发展前景。

目前，风速的模拟与结构形式毫不相关，也就是说不论什么样的结构形式，只要所在的场地地貌相同，平均风速相同，模拟出来的脉动风速时程都是相同的，这与实际情况存在一定差异。脉动风速与结构形式的关联值得进一步研究。

参考文献：

[1]MARIO D P.Digital Simulation of Wind Field Velocity[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74-76:91-100.

[2]RICE S O.Mathematical analysis of random noise[C]// Selected papers on noise and Stochastic processes,N.Wax,et.Dover Publish Inc.New York,1954:133-294.

[3]SHINOZUKA M.Simulation of multivariate and multimensional random processes[J].Journal of the Acoustical Society of America.1971,49(1):357-367.

[4]YANG J N.Simulation of random envelope processes[J].Journal of Sound and Vibration,1972,21(1):73-85.

[5]王之宏.风荷载的模拟研究[J].建筑结构学报，1994，l5(1)：44-52.

[6]司敏，陈波，刘元志，等.斜拉人行桥多维脉动风荷载模拟研究[J].武汉理工大学学报，2014，36(8)：82-87.

[7]李志国，何能，廖海黎，等.数值模拟脉动风场在斜拉桥抖振响应分析中的应用[J].铁道建筑，2014(5)：9-12.

[8] 汪瑞.结合工程实例的扣塔脉动风荷载模拟及风振响应分析[J].特种结构，2012，29(4)：124-127.

[9]曹玉生，包格瓦日图.基于Matlab的大型兆瓦级风电机脉动风速时程数值模拟[J].内蒙古工业大学学报，2013，32(4)：278-284.

[10]舒兴平，严兴华，邹浩.通信角钢塔脉动风荷载模拟及风振响应分析[J].工业建筑，2011，41(4)：119-123.

[11]曹丽珍.高耸钢塔结构风振响应分析[J].四川建材，2014，40(4)：59-62.

[12]李正农，刘艳萍，王莺歌，等.近地边界层脉动风数值模拟[J].湖南大学学报:自然科学版，2010，37(4)：6-10.

[13]DEBASIS K,SAMIT R C,MASANOBU S.Probabilistic Engineering Mechanics[J].2012(29):167-175.

[14]HUANG G Q,LIAO H L,LI M S.New formulation of Cholesky decomposition and applications in stochastic simulation[J].Probabilistic Engineering Mechanics,2013(34):40-47.

[15]陈俊儒，吕西林.上海中心大厦脉动风荷载模拟研究[J].力学季刊，2010，31(1)：92-100.

[16]胡亚琪.输电塔架结构风振响应分析[D].广西：广西大学，2011.

[17]陈建芳，陈家豪，何志.基于AR法的输电塔风振响应时程分析[J].广西工学院学报，2013，24(2)：74-77.

[18]马骏，周岱，李磊，等.风时程模拟的高效高精度混合法[J].工程力学，2009，26(2)：53-59.

[19]曾少青.宁波国际会展中心屋盖结构风振响应分析[D].广州：华南理工大学，2010.

[20]武秀根，郑百林，刘曙光，等.大型冷却塔的风致振动数值分析[J].力学季刊，2011，32(1)：91-96.

[21]刘亚庆.Kiewitt型索弯顶结构的静力性能与风振响应分析[D].广州：华南理工大学，2013.

[22]CHARLES K C.An Introduction to Wavelets[Z].Academic Press Inc.1992.

[23]ASSMOAH F.Discrete Wavelet Analysis of Signal[J].International Journal of Engineering Education，1999 (36):255-264.

[24]李峰，窦鹏，王磊.风荷载模拟方法探讨[J].水利与建筑工程学报，2009，7(4)：57-59.

[25]KAREEM A,KIJEWSKI T.Time-frequency analysis of wind effects on structures[J].Journal of wind engineering and industrial aerodynamics，2002(90):1435-1452.

[26]吴筑海，马骏，周岱，等.空间结构风时程模拟及分析[C]//第四届全国现代结构工程学术研讨会论文集.宁波：[出版地不详]，2004.

[27]韩艳，陈政清.利用小波逆变换模拟随机风场的脉动风[J].振动工程学报，2007，20(1):52-56.

[28]YAMADA M,OHKITANI K.Orthonormal wavelet analysis of turbulence[J].Fluid Dyn.Res.，1991(8):101-115.

[29]ZELDIN B A,SPANOS P D.Random field representation and synthesis using wavelet bases[J].Journal of Applied Mechanics,1996,63(12):946-952.

[30]AKSOY H,TOPRAK Z F,AYTEK A,et al.Stochastic generation of hourly mean wind velocity data[J].Renewable energy,2004(29):2111-2131.

[31]陈艾荣，王毅.基于小波方法的随机脉动风模拟[J].同济大学学报:自然科学版，2005，33(4):427-431.

[32]周岱，马骏，吴筑海，等.空间结构三维风速时程模拟及其小波分析[J].工程力学，2006，23(3):88-92.

[33]柳杰，周岱，黄剑伟，等.大跨空间结构风模拟的改进方法及小波识别[J].振动与冲击，2006，25(4):21-24.

[34]郭立伟，张文福，孙晓刚，等.电视塔抗风控制[J].东北林业大学学报，2007，35(8):60-62.

[35]李宏男，伊廷华，王国新.小波分析在结构风工程中的应用[J].振动与冲击，2008,27(9)：11-16.

[36]刘锡良，周颖.风荷载的几种模拟方法[J].工业建筑，2005，35(5)：81-85.

[37]邓文旭.结构的脉动风荷载模拟方法探讨[J].安徽建筑，2007(4)：85-87.

[38]CEBON D.Interaction Between Heavy Vehicles and Roads[Z].SAE,Inc.1993.

[39]陈果，翟婉明.铁路轨道不平顺随机过程的数值模拟[J].西南交通大学学报，1999，34 (2):138-142.

[40]侯传亮，张永林.工程平稳随机过程的数值模拟研究[J].武汉工业学院学报，2003,22(3)：27-29.

(责任编辑周江川)

本文引用格式：程华，钟华生，周凌，等.脉动风速时程数值模拟[J].兵器装备工程学报，2016(4):143-148.

Citation format:CHENG Hua, ZHONG Hua-sheng, ZHOU Ling, et al.Numerical Simulation of Fluctuating Wind Velocity Time Series[J].Journal of Ordnance Equipment Engineering,2016(4):143-148.

Numerical Simulation of Fluctuating Wind Velocity Time Series

CHENG Huaa, ZHONG Hua-shenga, ZHOU Linga, WANG Longb

(a.Department of Civil Engineering; b.Brigade of Cadet,Logistic Engineering University, Chongqing 401331, China)

Abstract:Wind load was the key control load and its dynamic effect for high-rise and long-span soft structures which were wind-sensitive must be considered. The general situation in numerical simulation of fluctuating wind velocity time history was introduced including traditional harmony superposition method, linear filtering method, as well as wavelet analysis, inverse Fourier transform. Then, fluctuating wind velocity time series of cable-truss mobile hangar was simulated in AR model. Finally, the advantages and disadvantages of various methods were summarized and the prospect of wind velocity time history simulation was looked forward.

Key words：fluctuating wind velocity time series；numerical simulation；harmony superposition method; linear filtering method; wavelet analysis

文章编号：1006-0707(2016)04-0143-06

中图分类号：TU312.1

文献标识码：A

doi:10.11809/scbgxb2016.04.035

作者简介：程华(1958—)，男，工学博士，教授，主要从事军事工程抢修抢建技术与装备研究。

基金项目：重庆市基础与前沿研究计划项目(cstc2013jcyjA30013)

收稿日期：2015-09-14；修回日期：2015-10-10

【基础理论与应用研究】