善用练习培养学生的有序数学思维

江苏太仓市新区第二小学（215413）桂俊婵



善用练习培养学生的有序数学思维

江苏太仓市新区第二小学（215413）桂俊婵

［摘要］练习是检查学生知识掌握情况的重要手段，也是培养学生有序数学思维的重要载体。教师在练习中要引导学生经历从无序到有序、从简单到复杂、从表面到本质、从多样到优化的思维过程，帮助学生掌握知识和技能，培养和发展学生的有序数学思维能力。

［关键词］有序数学思维练习培养

小学生，特别是中低年级的学生，受心理年龄、无关因素等多方面原因的干扰，在面对具体的数学问题时，难以做到有序思考，很多时候不是凭直觉猜测，就是依赖于思维的拼凑，没有确实的依据以及有效的方法。这样往往会造成思维混乱、考虑问题片面。因此教师一定要注意培养学生的有序数学思维，提高学生的思维能力。在教学中，教师要将有序数学思维的培养渗透在每一节课和每一次练习中。

当今的小学数学课堂教学中，教师在课堂上都会针对教学的知识点设计相关的练习，通过练习帮助学生巩固所学知识、学会运用知识以及查漏补缺。练习是检验学生知识掌握情况的重要手段，也是培养学生有序数学思维的重要载体。教师在课堂教学中要善于设计和开发练习，运用练习帮助学生掌握知识和技能，培养和发展学生的有序数学思维能力。

一、从无序到有序，数学思维过程有序呈现

有序性是有序数学思维的基本特征。当学生的思维受各方面因素的影响，导致考虑问题片面甚至反复纠结时，教师可以引导学生逐步整理清楚各因素之间的关系，使之有序化，促使学生思考，并做到不重复、不遗漏地考虑完所有的情况。通过引导学生有序地想、有序地尝试、有序地表达，能使学生的数学思维从混沌逐渐过渡到有序的状态。

例如，在某次练习中，我给出3、6、9这3个数，要求学生进行组数练习，把这3个数能够组成的所有三位数都列出来。一开始很多学生都是随机地尝试，想到一个是一个，结果出现了严重的重复或遗漏的情况。如果学生如果能做到有序思考，在明确要求是组成三位数的情况下，先确定百位，再依次确定十位和个位，那么解题的过程就会简洁且有效许多。如，当百位是3时，十位可以是6或9；如果十位是6，则个位只能是9，所以组成的三位数为369；而如果十位是9，则个位为6，所以组成的三位数为396……这样逐一地、有序地将所有情况罗列出来，思维过程全面且严密，大大地提高了做题的效率。

二、从简单到复杂，数学思维过程条理清晰

在教学中，基础较薄弱的学生在面对稍微复杂的练习时一般很难找到解决问题的突破口，即便是对着题目苦思冥想也不得其解。数学教学除了要使学生习得知识外，还要使学生掌握一些基本的解题方法，如从易到难，从简单的入手寻找解决问题的突破口，一点一点地把难题解决掉。这样一方面能够帮助学生明确解决问题的思路，另一方面也能让学生习得寻找突破口的策略，帮助学生树立学好数学的信心。

例如，对于“画与已知长方形面积相同的平行四边形和三角形”这道练习，教师可引导学生根据这三种图形面积之间的关系去思考。因为长方形的面积等于长乘宽，平行四边形的面积等于底乘高，三角形的面积等于底乘高除以2，所以可以从较为简单的平行四边形去突破。长方形的面积确定，那么它的长和宽的范围也基本能确定。画与长方形面积相同的平行四边形相对而言比较简单，学生基本都能画出。画出了平行四边形之后再思考三角形可以怎样画，这时只要根据三角形与面积相等的平行四边形之间的关系去解决即可。等底时，三角形的高只需是平行四边形的2倍即可；等高时，三角形的底是平行四边形底的2倍即可满足。在情况允许的条件下，教师还可引导学生思考其他的可能情况。这样从简单的入手，按从易到难的思路来思考问题，就能够使其数学思维更具条理性，也使学生乐于思考。

三、由表面到本质，数学思维过程逐步深化

数学课程标准明确提出：“数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。”数学教学不能仅局限于使学生掌握基础知识和技能，还要注重培养学生的思维能力，促使其数学思维纵向发展。然在当今的数学教学中，一些教师只片面地注重结果的正确与否，忽视了学生思维过程的纵向培养。

例如，下面哪些三角形的面积是平行四边形面积的一半？

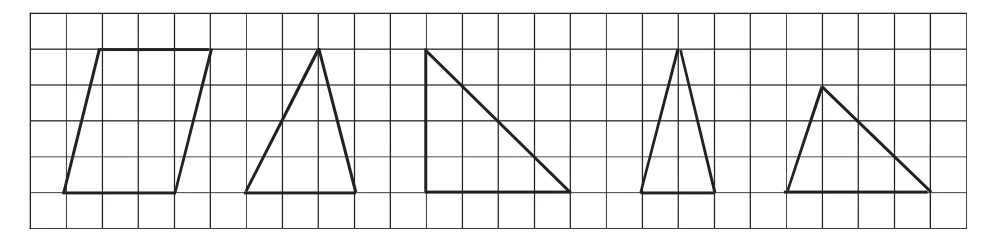
很多教师为了保险起见，一般都要求学生算出每个图形的面积再进行比较。我认为设计这道习题的意图不是让学生中规中矩地先计算出结果再比较，而是想让学生灵活运用所学知识，根据具体情况去快速判断，获取结果。尽管一些学生在解决这道题时是通过计算得出结果，但是如果教师能引导学生根据平行四边形以及三角形的面积以及底和高之间的关系去思考，明确等底等高的三角形面积是平行四边形的一半，同样也能解决这个问题。有时尽管底和高都不相同，但只要底乘高的积相同，三角形的面积也依旧是平行四边形面积的一半。这样在具体的练习中从表面着手，挖掘其背后的实质，不仅能够使学生更深入的思考知识本质之间的联系，帮助学生更好的掌握基础知识，也是进行有序数学思维训练的重要途径。

四、从多样到优化，数学思维有效提升

同样的问题，不同的学习个体因其学习的起点不同，思考的角度就会存在差异，解决问题的思路和方法也不尽相同。很多教师在教学中能够尊重学生的个体体验，关注方法多样化，沟通不同方法之间的联系，让学生用自己喜欢的方法解决问题。我认为学生数学思维的发展过程应该是一个螺旋递进的过程，数学思维的培养过程应该是一个不断比较的优化过程。只有做到了有序地递进，其数学思维的发展才是最有效的。

例如，如图，连接长方形4条边上的中点，可以得到一个平行四边形，求平行四边形的面积。

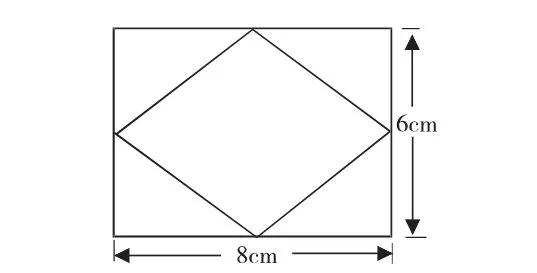
在计算平行四边形的面积时，很多学生都将平行四边形分成了三角形再计算。有的算了两个三角形的面积，也有的算了四个三角形的面积，只要求出每个三角形的底和高都能够得出结果。但这道题中还有一种更简便的方法，用8×6÷2就能求出平行四边形的面积。因为若将平行四边形分成两个三角形，那每个三角形的面积就是所在的小长方形面积的一半。因为有两个这样的三角形，所以两个三角形的面积（平行四边形的面积）就是整个长方形面积的一半。

当学生呈现出不同的计算方法后，教师要善于引导学生对不同的方法进行比较，深化学生对知识本质的理解，并在理解的基础上优化解题思路，使学生的数学思维有序提升，达到对数学思维的不断优化的目标。

总之，练习是呈现学生思维过程的重要载体，在教学中教师要善于开发练习，巧用练习促使学生充分经历有序数学思维的过程，提升学生的思维品质。

（责编吴美玲）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）14-067