高中数学教材二次开发案例展示

刘祥波

【摘要】新课标理念下，教师的角色定位是学生课堂学习的组织者、引导者、合作者和课程、教材的二次开发者.如何开发教材，创造性地使用教材，使之更加符合不同的施教对象，本文从具体实例出发，给出了一种可行的方案.【关键词】新课标；教材；二次开发

新课改在教师如何使用教材上赋予了更大的权力，要求教师转变传统“圣经式”的教材观，形成结合学生实际需要和课程标准对教材进行深加工和创造性使用的“工具观”或“材料观”，即教师要进行“教材二次开发”.

从心理学角度讲，教材二次开发是贯穿课前、课中、课后整个教学过程以思维为主导的智力活动，教师教材二次开发能力是指教师结合学生的实际情况和自身的经验，在整个教学过程中，及时洞察学生的特点，运用不同形式思维，对教材的内容进行分析、生成和反思的能力.

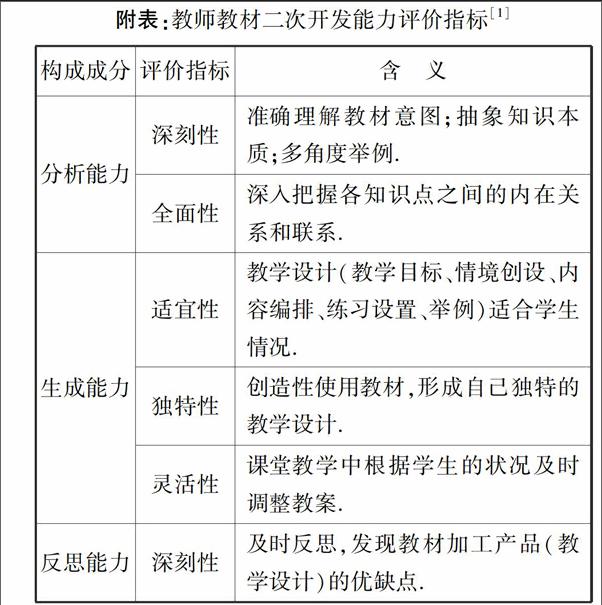
附表：教师教材二次开发能力评价指标[1]

构成成分[]评价指标[]含义

分析能力[]深刻性[]准确理解教材意图；抽象知识本质；多角度举例.[BH]

全面性[]深入把握各知识点之间的内在关系和联系.[ZB）]

生成能力[]适宜性[]

教学设计（教学目标、情境创设、内容编排、练习设置、举例）适合学生情况.[BHG11mm]

独特性[]

创造性使用教材，形成自己独特的教学设计.[BH]

灵活性[]

课堂教学中根据学生的状况及时调整教案.[ZB）]

反思能力[]

深刻性[]

及时反思，发现教材加工产品（教学设计）的优缺点.[BG）F]

依笔者浅见，对教材的例、习题进行重新（二次）设计是实现教材二次开发的有效途径.下面依据个人的教学经历，把人教B版教材必修四《倍角公式》一节的例题、习题进行重新设计.若有不当，敬请指正.1例题和习题设计的指导思想

1.1本节在教材中的地位和教学要求

（1）从本节在教材中的地位来看，它是上节课“和角公式”的继续和深化，同时又是下一节“半角公式”学习的基础和铺垫.

（2）从本节的教学要求上看，本节要求能从两角和的三角公式推出倍角公式，体验公式的推导过程，体会蕴含其中的数学思想方法，发展学生的逻辑推理能力和运算能力.

1.2 例、习题设计的指导思想

（1）适当注意例题数目.现行教材上只有两个例题，我们觉得少了一点，可以增加到三个.可以让师生有相对更多的选择余地.

（2）通过例题、习题，突出对运算能力和恒等变形能力的考查，以培养学生的运算能力和逻辑推理能力.

（3）重视对含有重要数学思想方法能一题多解的例题的选编.这样的例题，能发挥引领和带动作用，提高学生的思维发展水平，促进学生数学素养的形成.2例题设计

例1已知sin α=513，α∈（π2，π），求sin 2α、cos 2α、tan 2α的值.

解因为sin α=513，α∈（π2，π），所以

cos α=-1-sin2α=-1-（513）2=-1213，

sin 2α=2sin αcos α=2×513×（-1213）=-120169，

cos 2α=cos2α-sin2α=（-1213）2-（513）2=119169，

tan 2α=sin 2αcos 2α=-120169÷119169=-120119.

设计意图本例题选自于课本例1.

选择这道例题的原因是：

1. 5，12，13是一组勾股数，学生比较熟悉，利于学生运算，利于培养学生的运算能力，特别是口算能力；

2.求tan 2α，还可以直接利用正切的倍角公式，体现了一题多解，利于培养学生的发散思维能力.

例2已知cos（α-β）=-45，cos（α+β）=45，且（α-β）∈（π2，π），（α+β）∈（3π2，2π），求cos 2α.

解：因为cos（α-β）=-45，（α-β）∈（π2，π），所以

sin（α-β）=1-cos2（α-β）=1-（-45）2=35，

因为cos（α+β）=45，（α+β）∈（3π2，2π），所以sin（α+β）=-1-cos2（α+β）=-1-（45）2=-35，

所以cos 2α=cos（α+β）+（α-β）

=cos（α+β）cos（α-β）-sin（α+β）sin（α-β）

=45×（-45）-（-35）×（35）

=-1625+925

=-725.

设计意图这个例题选自课本课后练习B第2题.

选择这个例题的原因是：

1.角的变换是三角恒等变换的关键和核心.抓住条件中的角和结论中角的等量关系，是解题的关键.这里，通过（α+β）+（α-β）=2α，把求cos 2α的问题，转化为求两角和的余弦问题.

2.解题过程体现了转化与化归的重要数学思想和整体代换的重要数学方法.

这个例题是三角恒等变形的经典例题，建议选用.

例3证明等式：sin 2θ+sin θ2cos 2θ+2sin2θ+cos θ=tan θ.

证明：左边=sin 2θ+sin θ2（cos2θ-sin2θ）+2sin2θ+cos θ=sin θ（2cos θ+1）cos θ（2cos θ+1）=tan θ=右边.

设计意图这个例题选自课本例2.

选择这个例题的原因是：

1.通过本例题意在向学生展示：证明这个三角恒等式，其实就是体现化弦为切、化倍角2α为单角α、化分式为整式、化复杂为简单的转化思想；

2.根据等式左边分母的结构，强调cos 2α公式的选择性，体现了对学生观察问题、分析问题能力的考查.

3.本题还可有别的更多证法，建议通过设立“思考与讨论”栏目的形式鼓励师生探究.3课后习题设计

练习A

1.求下列各式的值：

（1）2sin 67°30′·cos 67°30′； （2）cos2π8-sin2π8；

（3）2cos2π12-1；（4）1-2sin275°；

（5）2tan 22.5°1-tan222.5°；（6 ） sin 15°cos 15°.

选用原因这组求值题来自于教材，建议保留.

（1）题中的角都是常见特殊角的半角，化简出来的三角函数值都是常用的，有利于学生对这些重要三角函数值的复习和巩固；

（2）求值的过程体现了对公式的逆用和变形用，有利于考查学生的逆向思维能力和发散思维能力，发展其逻辑思维能力和运算能力.

2.已知cos α=-1213，且α∈（π2，π），求cos 2α，sin 2α的值.

3.已知tan α=12，求tan 2α，cot 2α的值.

4.求函数y=cos2x-sin2x的最小正周期、最大值和最小值.

选用原因这三个题目都是保留了教材上原题.它们的难度较小，直接利用公式就可计算出来.非常适合于新授课的练习.

练习B

1.化简：

（1）（sin α-cos α）2；（2）sinθ2cosθ2；

（3）cos4φ-sin4φ；（4）11-tan θ-11+tan θ.

选用原因对公式进行变形是掌握公式、巩固公式的重要方法，并且这些变形结果也是今后学习要经常用到的.

2.已知sin 2α=513，π4<α<π2，求sin 4α、cos 4α、tan 4α的值.

设计意图

（1）帮助学生理解“倍角”的含义，体会倍角关系的相对性；

（2）培养学生的特殊数据处理能力（特别是常见的勾股数）；

（3）可以通过尝试一题多解，培养学生的发散思维能力.

3.已知α、β为锐角，sin α=817，cos（α-β）=2129，求cos β.

设计意图

（1）考查角的整体代换的熟练程度和方法的选择性（如果不用整体代换，应该怎样做？简练程度怎样？）；

（2）考查了较为复杂的数据计算，培养学生的运算能力；

（3）进一步让学生体会和领悟转化和化归的数学思想.4本节例、习题设计的体会与建议

4.1两点体会

（1）本节课公式多，公式的变形多，历来是学生学习的难点.我们的例、习题设计遵循了先易后难、循序渐进的原则，力争利用有限的例题和习题涵盖常见题型，体现了教材对师生的人文关怀，同时也便于师生使用；

（2）注重选用内涵丰富的例、习题，如数值特殊、方法重要（如角的等值代换）、思想深刻的题目，力争使所选的例、习题能促进学生对公式及其变形的掌握，促使学生知识系统和方法系统的完善.

4.2一个建议：

课本P144 B 第3题和第4题，从我们多年来的新授课教学实践看，学生接受起来比较困难.

第3题：求cos 20°cos 40°cos 80°的值.（提示：乘以并除以2sin 20°）

第3题的结构特殊，解法相对固定、单一，体现了一定的技巧性，如果没有教材的提示，学生更是无从下手，即便是按照课本上的提示，学生做对了，以后遇到可能还是不会.

第4题：圆心角为60°的扇形AOB 的半径为1，C 是AB 弧上一点，作矩形CDEF，如右图，当C 点在什么位置时，这个矩形的面积最大？这时的∠AOC 等于多少度？

第4题是个函数“应用题”，没有给出具体的面积表达式，要学生自己推导，而这个建模的过程并不容易！并且，得到的面积函数要求出最大值，还要经过降幂、合并（利用辅助角公式）等工作，显然，这是一个综合题，放在新授课课后的位置，难度太大.

建议把这两个题目放在习题32B或章末的“巩固与提高”栏目中，供学生选做.

教学实践的经验告诉我们，教师只有根据学生的实际情况，在理解课标精神、教材编写意图的基础上，合理取舍教学内容，设计有自己个性的、符合学生实情的教学方案，实现对教材的二次开发，才能更好地促进我们的教与学.

参考文献

[1]张莉，李西营.中小学教材二次开发能力评价指标体系的构建[J].课程·教材·教法，2015（10）

2.普通高中课程标准实验教科书数学（4）人民教育出版社2007年4月第二版

3.普通高中数学课程标准（实验）

4.章建跃.中学数学课改的十个论题 .中学数学教学参考20103

5.涂荣豹.谈提高对数学教学的认识——兼评两节数学课.中学数学教学参考 20061-2