平均数的推广

李 会 平

(1. 安徽绿海商务职业学院 基础部，安徽 合肥 230601；2.合肥师范学院，安徽 合肥230601)



平均数的推广

李 会 平1,2

(1. 安徽绿海商务职业学院 基础部，安徽 合肥 230601；2.合肥师范学院，安徽 合肥230601)

摘要：文章运用函数论方法研究统计活动中常用的平均数，先定义LHP平均数，再给出LHP平均数的性质与LHP平均数比较定理的应用。

关键词：平均数；不等式；导数；凹凸性

平均数是统计活动常用的一个重要概念，长期以来，数值平均数仅仅包括算术平均数、几何平均数与调和平均数。本质上，平均数与函数有紧密的联系，以下用函数论的方法推广平均数的概念。

1平均数概念的推广

为严密推广平均数，有必要先介绍封闭集合与封闭定义域。

定义1设函数f(x)在集合D上有定义，称集合D为函数f(x)的封闭集合，若任意给定xi∈D,i=1,2,…,n,存在ξ,η∈D，有

定义2若函数f(x)的封闭集合D为f(x)的定义域，则称D为函数f(x)的封闭定义域。

2LHP平均数的主要性质及其证明

为证明LHP平均数的性质定理，先给出几个引理及相关概念。

引理1如果函数y=f(x)在有定义的集合D上为严格单调函数，那么y=f(x)在D上有反函数y=f-1(x)。

引理2[1]设函数y=f(x)在区间I上连续可导。

(1)如果在I上f′(x)>0，那么函数y=f(x)在I上严格单调增加；

(2)如果在I上f′(x)<0，那么函数y=f(x)在I上严格单调减少。

引理3[2]设f(x)为定义在区间I上的二阶可导函数，若f″(x)>0[f″(x)<0]，x∈I，则在I上f(x)为严格凹(凸)函数。

定义4称在有定义的集合D内严格增严格凸且满足f(xy)=f(x)f(y)(∀x,y∈D)的正值函数f(x)为D内的平衡函数。

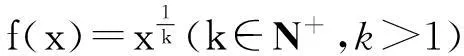
下面给出LHP平均数的性质定理。

证明对于函数f(x)=x，封闭集合为

(0,+∞)，反函数f-1(x)=x，

对于函数f(x)=lnx，封闭定义域为(0,+∞)，反函数f-1(x)=ex，

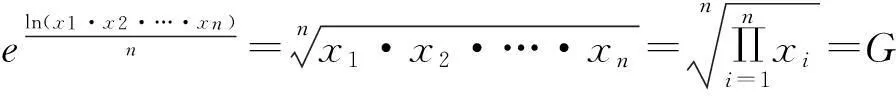
注定理1表明LHP平均数为数值平均数的推广。

定理2(LHP平均数线性定理)线性函数的LHP平均数为算术平均数。

证明当函数f(x)为线性函数时，f-1(x)也为线性函数，此时有

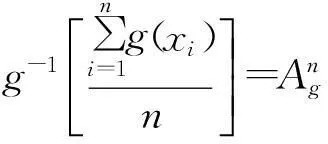
定理4(LHP平均数比较定理)设函数f(x)在封闭集合D内二阶可导,

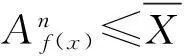
当且仅当x1=x2=…=xn时，等号成立。

证明(1)如果在D内f′(x)>0[f′(x)<0]且f″(x)<0[f″(x)>0]，f(x)为D内严格增(减)函数且为D内严格凸(凹)函数，显然，f-1(x)也为严格增(减)函数，由引理4得到

当且仅当x1=x2=…=xn时，等号成立。

即得

当且仅当x1=x2=…=xn时，等号成立。

即得

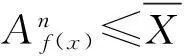
当且仅当x1=x2=…=xn时，等号成立。

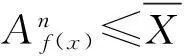
(2)如果在D内f′(x)>0[f′(x)<0]且f″(x)>0[f″(x)<0]，f(x)为D内严格增(减)函数且为D内严格凹(凸)函数，显然，f-1(x)也为严格增(减)函数，由引理4得到

当且仅当x1=x2=…=xn时，等号成立。

即得

当且仅当x1=x2=…=xn时，等号成立。

即得

当且仅当x1=x2=…=xn时，等号成立。

注LHP平均数比较定理揭示出，LHP平均数是函数性态的又一重要方面，可以用导数研究LHP平均数的某些性质。

推广此定理可以得到以下定理。

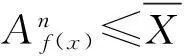
证明由定理4证明过程即得。

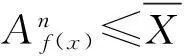
当且仅当x1=x2=…=xn时，等号成立。

由f-1(x)为严格增函数即得

3LHP平均数比较定理应用举例

例1对于函数f(x)=lnx,x>0，f′(x)=

例3对函数f(x)=xk,x>0,k>1且

k∈N+，f′(x)=kxk-1>0，f″(x)=k(k-1)xk-2>0，有f′(x)f″(x)>0，由定理4得当k>1时，有

注由以上例题知从LHP平均数比较定理可直接得到一些常见不等式。

f′(x)=cosx>0，f″(x)=-sinx<0,

参考文献:

[1] 李忠. 高等数学[M]. 北京：北京大学出版社，2009:181.

[2] 教育部高等教育组专家.高等数学[M]. 北京：高等教育出版社，1999:166.

[3] 陈纪修. 数学分析[M]. 北京：高等教育出版社，1999：176.

Generalization of Average

LI Hui-ping1,2

(1.Elementary Department , Anhui Lvhai Vocational College of Business, Hefei, Anhui 230601,China；2. Hefei Normal University, Hefei, Anhui 230601, China)

Abstract:The paper studies statistical averages by using function theory, the LHP average is defined firstly, then natures of LHP average and the application of the LHP average comparison theorem are given.

Key words:average, inequality, derivative, convexity

文章编号：1007-4260(2016)01-0016-03

中图分类号：O13

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2016.01.005

作者简介：李会平，男，安徽望江人，硕士，安徽绿海商务职业学院基础部讲师，主要科研方向为复分析。E-mail: 6789987699@163.com

*收稿日期：2015-07-17

网络出版时间：2016-03-15 17:05网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160315.1705.005.html