基于Laplace方程的球面正交曲线格网生成方法
卢 付 强,宋 志 尧,雷 梦 玲,丁 凯 孟
(1.南京师范大学虚拟地理环境教育部重点实验室,江苏 南京 210023;2.南京师范大学大规模复杂系统数值模拟江苏省重点实验室,江苏 南京 210023;3.江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023)
基于Laplace方程的球面正交曲线格网生成方法
卢 付 强1,2,3,宋 志 尧1,2,3,雷 梦 玲1,3,丁 凯 孟1,3
(1.南京师范大学虚拟地理环境教育部重点实验室,江苏 南京 210023;2.南京师范大学大规模复杂系统数值模拟江苏省重点实验室,江苏 南京 210023;3.江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023)
为克服基于传统经纬度格网的全球海洋及大气数值模式产生的极点问题,同时顾及全球格网编码便捷及信息查询,该文将立方体球心投影的格网经球极投影转换到二维平面区域,再应用Laplace方程数值求解生成正交曲线格网;然后采用球极逆投影,得到球面上一种新的正交曲线格网。通过与等角球心投影、保角变换两种球面格网生成方法的结果相比较,从格网两边的长度、单元的面积、正交性等指标进行统计分析,对所生成格网的质量进行评价。结果表明,等角球心投影法生成的格网单元大小较均匀,但正交性不理想;Laplace方程法生成的正交曲线格网稍优于保角变换法,可作为应用有限差分方法和有限体积方法的全球海洋及大气大尺度数值模拟的基础格网。
Laplace方程;球极投影;正交曲线格网;Neumann正交化
0 引言
随着全球气候逐渐变暖,极端天气现象发生的频率呈升高趋势,需对全球气候变化进行及时预测,以便采取可能的措施减小恶劣天气产生的危害。而这些预测在很大程度上依赖于全球大气模式、海洋模式的发展,因此需要构建一个理想的全球大气、海洋数值模型都适用的网格,以便进一步实现相互耦合的数值模拟。建立全球大气、海洋数值模型的第一步就需要选择一个好的全球离散网格。目前在大气、海洋数值模式中所采用的网格分为两大类[1]:一类是有结构网格,网格的排列结构纵横有序,相邻节点或网格单元的数目是固定的,易于结点(单元)的编号和布置变量,便于方程的离散和计算编程,如传统或退化的经纬度格网[2,3]、立方体球心投影网格[4,5]、阴阳交叠网格[6,7]等。另一类是无结构网格,即由任意三角形或六边形组成的网格,如基于正二十面体产生的球面三角网格[8,9]、球面正六边形网格[10,11]。此类网格在全球大气或海洋运动数值模型中得到了广泛应用,其主要优点是:整体上网格大小较均匀。但在这类网格上对数据进行操作,需要预先对每个网格建立索引、拓扑关系表,并且在这类网格上建立数值模型的求解方法通常较复杂。
正交曲线网格属于有结构网格,具有很多优点:首先,网格的编码与领域查询比较方便,模型方程组在正交曲线坐标系中的表达形式比较简洁;其次,便于数值有限差分方法或者有限体积方法的设计和实现等。许多大气数值模式建立在经纬度网格上,但是经纬度网格在趋于两个极点时经线收敛,除了谱变换方法,在采用基于格点的方法进行数值计算时会引发极点问题[12],同时也产生了解决这些问题的方法:高纬度滤波、半隐式半拉格朗日方法等。但是这些方法在全球海洋模式中却难以应用[13],所以必须考虑采用一种新的正交网格,采用数值求解Laplace方程组,结合球极投影方法,可生成球面正交曲线网格,既利于全球地理信息的表达,也适用于地球流体大尺度运动的数值模拟,同时也是生成三维球体准正交的曲面六面体网格的基础。
1 球面四边形网格生成方法
1.1 立方体球心投影方法
考虑球的内接立方体,分别在立方体的每个表面上建立局部二维笛卡尔坐标,然后做一个伸缩变换,将表面上每个点变换到外接球面上。假设球半径为R,可知立方体的边长2a与半径有关系式:
(1)
选取立方体中心为三维笛卡尔坐标系的原点,坐标轴X、Y、Z分别与立方体的前面、右面、顶面垂直(图1),其中左子图为立方体各面的展开图,右子图为立方体与外接球面在三维笛卡尔坐标系中的位置关系。记(x,y)为立方体每个表面上的局部二维笛卡尔坐标,有-a≤x,y≤a。

图1 立方体6个表面的展开图及其外接球面在三维笛卡尔坐标系中的位置
Fig.1 Layout of an open cube and the cube and its circum-sphere under 3D absolute Cartesian coordinates
从立方体表面变换到球面上有两种方法:
(1)立方体球心等距投影网格。直接对局部坐标进行等距网格剖分(图2),其中显示了在立方体表面X=a上的局部二维平面笛卡尔坐标(x,y)与半径为R的球面上点(X,Y,Z)之间的关系:
(2)
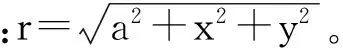
(2)立方体球心等角投影网格。首先对局部笛卡尔坐标做一个变换:

(3)

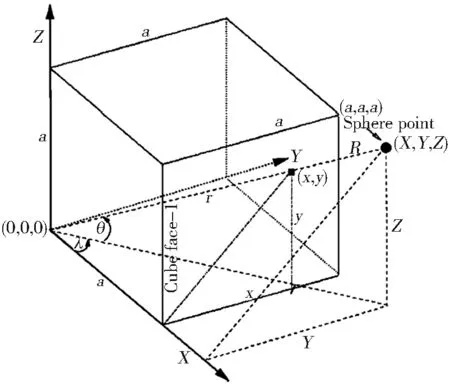
图2 立方体表面X=a上的点经过球心投影到球面上
Fig.2 Gnomonic projection of point on the cube surfaceX=ato the sphere surface
1.2 保角变换方法
应用保角变换将网格点在各复平面与球面之间变换时,网格的角度保持不变,并且除去8个角点,映射在每个网格点上是光滑的,保角变换方法的主要思想是先采用广义球极投影将球面上的点映射到复平面上,然后在复平面之间采用Taylor 级数展开式实现一系列复变换及逆变换[14]。保角变换生成的网格总体上正交性很好并且网格的长宽比接近1,即形状与正方形相近。但在8个奇点(角点)处,网格偏离正交性固定在30°,在角点附近的网格正交性也受到影响,正交性有所降低。尽管不如球面经纬网格在极点处收敛那么严重,严格的正交性要求将导致网格在8个奇点处收敛,可以对网格在局部进行拉伸以改善这种状况。
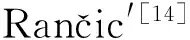
2 球面正交曲线网格生成
采用某种投影方法将球面上的网格变换到二维平面区域,然后借鉴平面上数值网格生成方法生成正交曲线网格,最后采用逆变换,将生成的网格变换到球面上。这个过程的主要思路可由图3描述。在一般情形下,采用投影变换后,网格的几何形状、面积、角度等属性都会发生变化。在此选取常用的3种地图投影变换方法:圆锥、圆柱及赤平投影[18,19],这些变换是保持正交性质的,即网格在球面与平面之间变换时,格网的角度不发生变化。
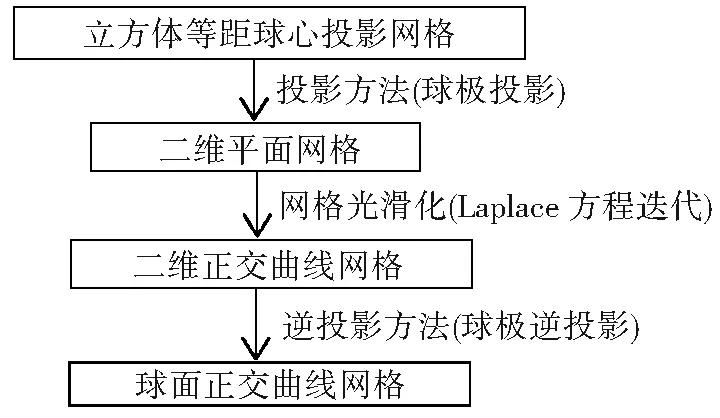
图3 算法的总体路线
Fig.3 The process of the presented algorithm
2.1 地图投影变换
由于立方体6个表面上的网格是对称的,所以只需在一个面上生成网格,然后采取合适的旋转变换就可得到覆盖整个球面的网格。在此选取赤道区域所在的一个球面区域作为基准面,图4显示了立方体球面前表面上初始网格分别经过Lambert正形圆锥投影、Mercator投影、赤平投影变换后的网格。立方体球面前表面上的格网关于格网中心具有四重对称性,从图4可看出:经过圆锥或圆柱投影,格网的四重对称性有损失;而经过赤平投影变换,格网的对称性得到保持,所以采用赤平投影或球极投影。
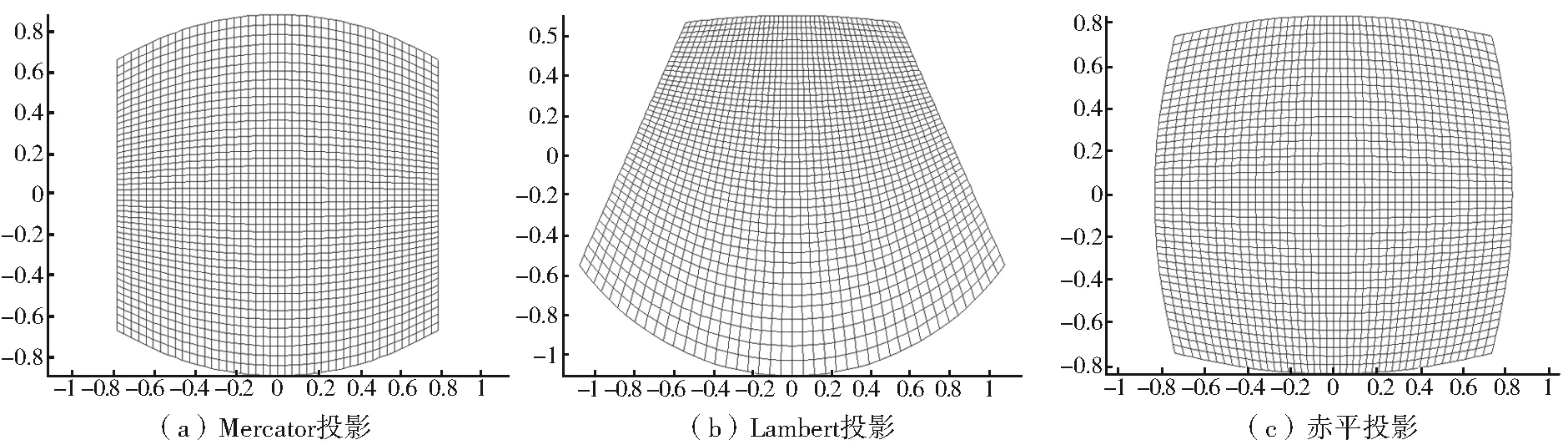
图4 经过圆柱、圆锥以及赤平投影变换之后,立方体球面前表面上格网点的分布
Fig.4 Distribution of gird points on front face of cubed sphere under Mercator projection,Lambert conformal conic projection and stereographic projection
2.2 Laplace微分方程方法
Laplace微分方程是一种椭圆形偏微分方程,椭圆形网格生成是通过求解拟线性椭圆形偏微分方程组的一种网格生成方法,可以对网格的光滑性及正交性进行控制。在生成球面网格时,初始网格取立方体等距球心投影网格,将在球面上物理网格的每个表面通过球极投影变换到二维的平面空间,然后对网格施加所需的限制条件,在投影平面上求解椭圆型偏微分方程组。在大部分基于有限差分方法的地球流体动力学数值模拟中,网格的正交性及网格尺寸的均匀性是最重要的,对网格施加正交性有Neumann条件限制和Dirichlet条件限制[20]两种方法。Neumann条件限制:网格点可以沿着每个面的边界滑动,而Dirichlet条件限制则是固定在边界上的点,通过调整网格内点并且保持网格尺寸的准一致性。Neumann条件限制通过要求未知量对两个参数的偏导数的乘积等于零来计算每个网格点沿网格边界的偏移量,但这种做法将导致网格单元在角点邻近区域趋于收敛,网格单元的面积偏小,可在局部对网格进行拉伸来改善这种状况。
假定一个二维初始变换W:(ξ,η)→(x,y),将计算空间[1,M]×[1,N]变换到物理空间Ω⊂R2,其中正整数M、N表示沿两个方向的网格点数目,网格线索引为ξ=1,2,…,M;η=1,2,…,N。初始变换常由一般的方法如代数方法中的超限插值技术得到。对于给定的初始变换,二维平面正交曲线网格的生成方法多采用数值求解下列拟线性偏微分方程组[21]:
g22(xξξ+Pxξ)-2g12xξη+g11(xηη+Qxη)=0
g22(yξξ+Pyξ)-2g12yξη+g11(yηη+Qyη)=0
(4)
其中:
(5)
(6)
(7)
其中:(x,y)为原二维物理区域中的网格点坐标,(ξ,η)为变换区域中网格点坐标。网格的度量项g11、g22分别表示网格沿两个方向的长度,g12可用于表示网格单元的角度大小。P、Q表示网格点疏密的控制函数,可通过改变P、Q对网格点的分布进行调整,若P=Q=0,则产生步长均匀的网格。
为了求解拟线性椭圆形方程组(4),需给出必要的边界条件,此处设置控制函数P=Q=0,取Neumann正交边界条件,允许边界点通过自由滑动达到边界上的正交。采用有限差分方法求解方程组(4),其中网格的度量项g11、g12、g22可以根据网格点坐标表达式预先计算出来,或者采用差分近似方法,系数中含有待求解函数的非线性项,采用前一次的迭代值计算这些系数,只对二阶偏导数以及与控制函数有关的导数项进行离散,采用中心差分近似,选取映射到计算空间中的离散步长Δξ=Δη=1,则:
(8)
(9)
采用超松弛迭代方法(SOR)求解上述方程组:
(10)
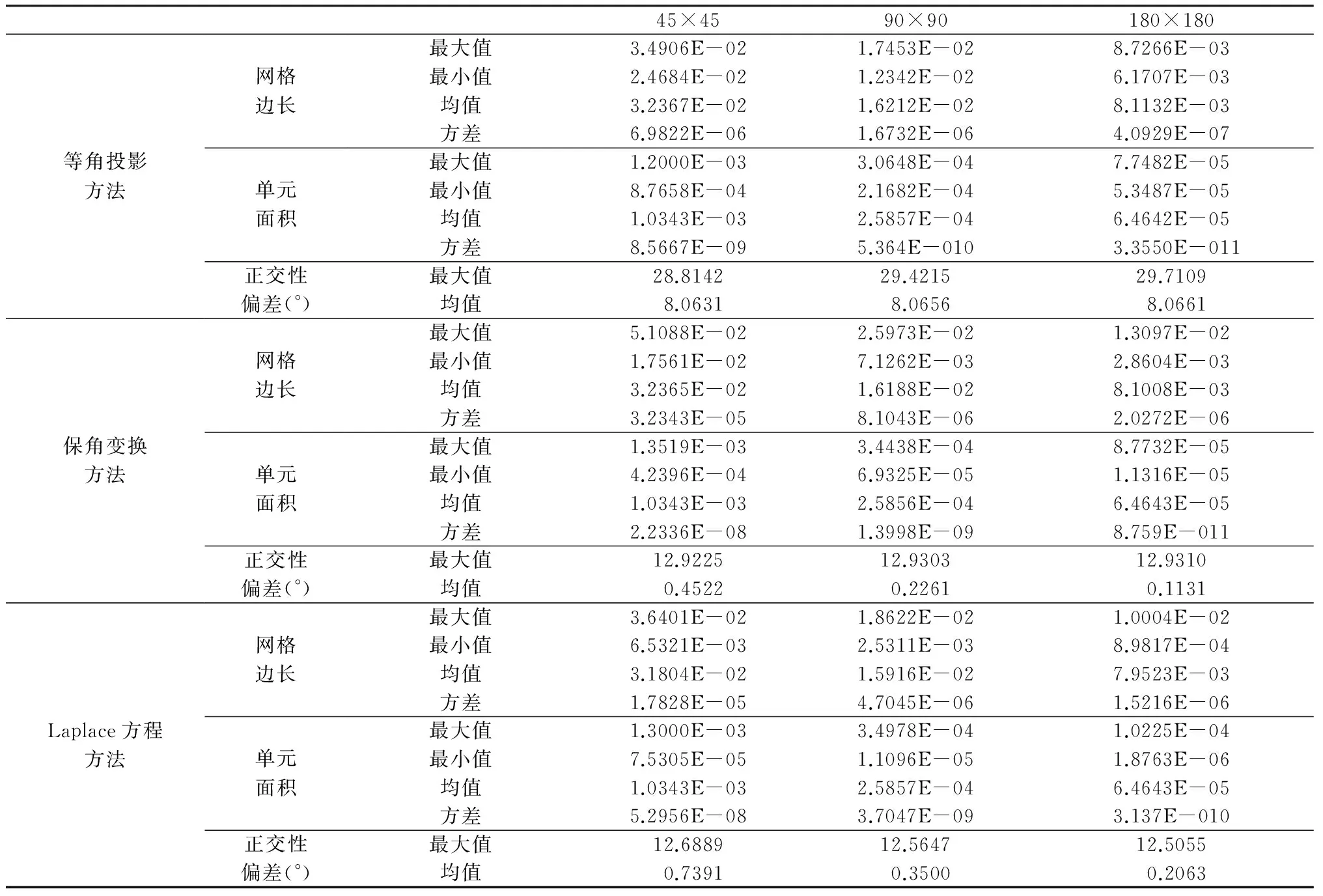
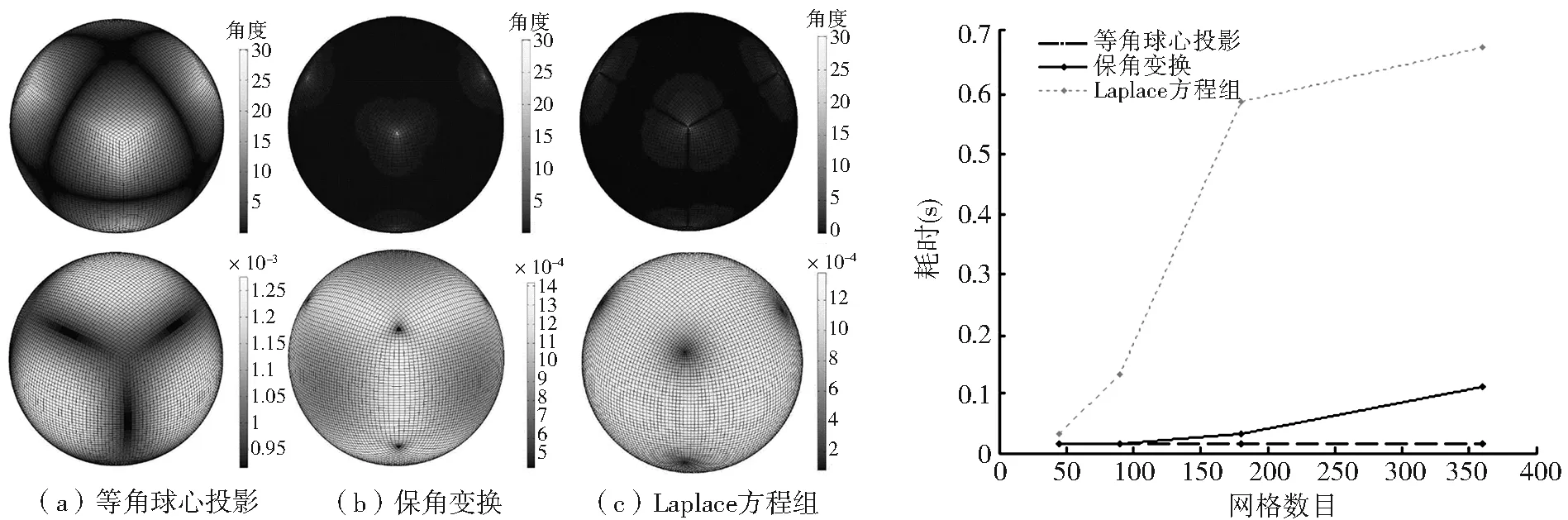
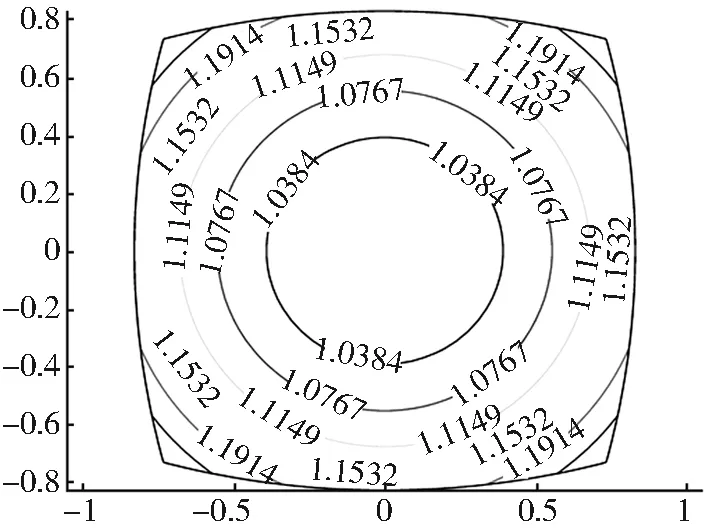
其中wi,j为松弛因子,应满足条件:0 2.3 Neumann正交边界条件 在求解区域边界上应该满足正交性条件: XξXη=0,在ξ=1,M (11) XξXη=0在η=1,N (12) 其中X表示网格点的二维坐标,采用有限差分方法对式(11)、式(12)进行近似求解,在迭代求解方程组时,每次循环中边界条件式都要进行更新。为了防止边界点滑动距离过大,超过其邻近点,需要设置临界值,特别是在钝角区域附近容易出现这种情形。合适的临界值对边界每个点的滑动距离起限制作用,一般要求在每次迭代过程中距离边界上最近两个邻近点的距离至多减少一半。 3.1 网格质量评价指标 网格的4个指标有:网格分别沿参数ξ方向与η方向的长度hξ,hη网格单元的面积大小area以及角度的正交性偏差DO: (13) (14) 3.2 计算结果分析 选取立方体的顶面Z=a作为基础,在其上建立局部二维笛卡尔坐标系(x,y),然后变换到半径为R的球面上。取a=1,采用北极投影,将立方体球心等距投影网格映射到与北极点相切的二维平面上,数值求解椭圆形微分方程组(4),采用Neumann正交边界条件(式(11)、式(12)),控制函数取值P=Q=0;然后再采用北极逆投影得到球面上的正交网格。图5给出了在球极投影下,各网格点处地图放大系数的等值线图,可以看出投影系数接近1 ,即网格经过球极投影后,几何度量变化不是很大。 目前,也可采用等角或等距球心投影方法以及保角映射方法生成立方体球面网格,但等角或等距球心投影产生的网格不具有正交性,而保角变换方法或求解椭圆形方程产生的网格正交性较好。下面给出上述方法生成网格的度量性质的比较结果。 选取网格单元数分别为45×45、90×90、180×180的情形时进行计算,相对应的空间分辨率大约为2°、1°、30°。表1给出了不同网格数时,分别采用等角投影方法、保角变换、Laplace方程方法生成网格的统计结果,包括网格单元最大边与最短边的长度、单元角度的正交性最大偏差以及平均偏差、网格单元面积的最大值和最小值。 图5 各网格点处的地图放大因子等值线 Fig.5 Map factor of each grid point after elliptic-smoothing under north polar stereographic projection 如果顶面的网格已经生成,则采用合适的旋转变换生成其他5个表面上的正交网格。图6显示了网格数在45×45×6时,采用等角投影方法、保角变换、 Laplace方程方法生成球面网格的正交性偏差及网格单元面积的变化。可看出保角变换、Laplace方程方法生成的球面网格非常相似,绝大多数网格的正交性偏差不超过10°,只是接近8个角点的网格单元的正交性偏差增大了一些,最大偏差发生在8个角点处。另外,从表1也可看出,保角变换与Laplace方程方法生成网格的统计量差别相当小,基本在同一个数量级。综合起来,在相同情形下,等角投影方法生成球面网格单元面积的大小较均匀,但正交性偏差较大;而保角变换、Laplace方程方法生成球面网格单元的面积总体上不如等角投影方法的均匀,尤其是在8个角点附近区域网格单元的面积偏小。 图 7 给出了网格逐次分半加密时,分别采用三种方法,Fortran编程的CPU消耗时间随网格数目的变化,可以看出在同等格网数目的条件下,求解Laplace方程组耗时最多,等角球心投影方法耗时最少,保角变换方法耗时稍多于等角球心投影方法。即便如此,生成空间分辨率为几分的格网最多时间耗费不过10 s,并且在发展全球大气或海洋数值模式过程中,网格生成是一次性的,这个时间是可接受的。 基于立方体球心投影网格,结合球极投影技术,采用Laplace方程组在球面上生成了一种广义正交曲线网格,并且对网格的质量进行分析评价。通过与等角球心投影、保角变换方法的结果进行比较,表明等角球心投影生成的网格单元大小较均匀,但网格不具有正交性;而保角变换方法、数值求解微分方程组生成的网格的正交性质较好,但在8个角点邻域的网格单元面积偏小。在应用于实际大气或海洋大尺度运动的具体数值模型中,这个缺陷可以通过对网格进行拉伸,或采用隐式时间积分方法来弥补。因此,这种广义正交曲线网格可用于地理空间数据的表达以及全球大气或海洋运动的数值模拟。 表1 在不同网格数情形下三种方法生成网格的统计结果 Table 1 Quality statistics of grids generated by three different methods with different cell-numbers 45×4590×90180×180等角投影方法保角变换方法Laplace方程方法网格边长单元面积正交性偏差(°)网格边长单元面积正交性偏差(°)网格边长单元面积正交性偏差(°)最大值3.4906E-021.7453E-028.7266E-03最小值2.4684E-021.2342E-026.1707E-03均值3.2367E-021.6212E-028.1132E-03方差6.9822E-061.6732E-064.0929E-07最大值1.2000E-033.0648E-047.7482E-05最小值8.7658E-042.1682E-045.3487E-05均值1.0343E-032.5857E-046.4642E-05方差8.5667E-095.364E-0103.3550E-011最大值28.814229.421529.7109均值8.06318.06568.0661最大值5.1088E-022.5973E-021.3097E-02最小值1.7561E-027.1262E-032.8604E-03均值3.2365E-021.6188E-028.1008E-03方差3.2343E-058.1043E-062.0272E-06最大值1.3519E-033.4438E-048.7732E-05最小值4.2396E-046.9325E-051.1316E-05均值1.0343E-032.5856E-046.4643E-05方差2.2336E-081.3998E-098.759E-011最大值12.922512.930312.9310均值0.45220.22610.1131最大值3.6401E-021.8622E-021.0004E-02最小值6.5321E-032.5311E-038.9817E-04均值3.1804E-021.5916E-027.9523E-03方差1.7828E-054.7045E-061.5216E-06最大值1.3000E-033.4978E-041.0225E-04最小值7.5305E-051.1096E-051.8763E-06均值1.0343E-032.5857E-046.4643E-05方差5.2956E-083.7047E-093.137E-010最大值12.688912.564712.5055均值0.73910.35000.2063 图6 不同投影生成网格的角度正交性偏差与网格单元面积大小 图7 三种方法的计算效率随网格数目的变化 Fig.6 Angle deviation orthogonality and cell area on equi-angular sphere grids based on different method Fig.7 The efficiency of three methods under different grid-numbers [1] STANIFORTH A,THUBURN J.Horizontal grids for global weather and climate prediction models:A review[J].Quarterly Journal of the Royal Meteorological Society,2012,138:1-26. [2] HOLLOWAY L,SPELMAN M J,MANABE J.Latitude-longitude grid suitable for numerical time integration of a global atmospheric model[J].Monthly Weather Review,1973,101(1):69-78. [3] FADEEV R Y.Algorithm for reduced grid generation on a sphere for a global finite difference atmospheric model[J].Computational Mathematics and Mathematical Physics,2013,53(2):237-252. [4] RONCHI C,IACONO R,PAOLUCCI P S.The "Cubed Sphere":A new method for the solution of partial differential equations in spherical geometry[J].Journal of Computational Physics,1996,124(1):93-114. [5] MCGREGOR J L.Semi-Lagrangian advection on a cubic gnomonic projection of the sphere[J].Atmosphere-Ocean,1997,35(1):153-169. [6] KAGEYAMA A,SATO T."Yin-Yang grid":An overset grid in spherical geometry[J].Geochem.Geophys.Geosyst.,2004,5,Q09005,doi:10.1029/2004GC000734. [7] 艾细根,刘宇迪,崔新东,等.基于球面阴阳网格数值计算研究进展[J].气象科技,2014,42(1):13-22. [8] TOMITA H,SATOH M,GOTO K.An optimization of the Icosahedral Grid modified by Spring Dynamics[J].Journal of Computational Physics,2002,183(1):307-331. [9] IGA S,TOMITA H.Improved smoothness and homogeneity of icosahedral grids using the spring dynamics method[J].Journal of Computational Physics,2014,258(1):208-226. [10] MIURA H,KIMOTO M.A comparison of grid quality of optimized spherical hexagonal-pentagonal geodesic grids[J].Monthly Weather Review,2005,133(10):2817-2833. [11] 童晓冲,奔进,汪滢.利用数值投影变换构建全球六边形离散格网[J].测绘学报,2013,42(2):268-276. [12] NAUGHTON M,COURTIER P. A pole problem in the reduced Gaussian grid[J].Quarterly Journal of the Royal Meteorological Society,1994,120:1389-1407. [13] ADCROFT A,CAMPIN J M,HILL C,et al.Implementation of an atmosphere-ocean general circulation model on the expanded spherical cube[J].Monthly Weather Review,2004,132:2845-2863. [15] NAIR R D,THOMAS S J,LOFT R D.A discontinuous Galerkin transport scheme on the cubed sphere[J].Monthly Weather Review,2004,133(4):814-828. [16] LU F,SONG Z,FANG X.Generation of Orthogonal Curvilinear Grids on the Sphere Surface Based on Laplace-Beltrami Equations[C].IOP Conference Series:Earth and Environmental Science,2014,(19) 012012. [17] PUTMAN W M,LIN S J.Finite-volume transport on various cubed-sphere grids[J].Journal of Computational Physics,2007,227(1):55-78. [18] 沈桐立,田永祥,葛孝贞.数值天气预报[M].北京:气象出版社,2003.60-71. [19] 王美玲,付梦印.地图投影与坐标变换[M].北京:电子工业出版社,2014.51-125. [20] THOMPSON J F,SONI B K,WEATHERILL N P.Handbook of Grid Generation[M].CRC Press,1999,ISBN 0-8493-2687-7. [21] SPEKREIJSE S P. Elliptic grid generation based on Laplace equations and algebraic transformations[J].Journal of Computational Physics,1995,118(1):38-61. Generation Method of Orthogonal Curvilinear Grids on Sphere Surface Based on Laplace Equations LU Fu-qiang1,2,3,SONG Zhi-yao1,2,3,LEI Meng-ling1,3,DING Kai-meng1,3 (1.Key Laboratory of Virtual Geographic Environment(Ministry of Education),Nanjing Normal University,Nanjing 210023;2.Jiangsu Key Laboratory for Numerical Simulation of Large Scale Complex Systems,Nanjing Normal University,Nanjing 210023;3.Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application,Nanjing 210023,China) In order to overcome the pole-problem induced by grid-based methods on traditional longitude-latitude grid for global atmosphere and ocean circulation models,a new kind of orthogonal curvilinear grids based on the gnomonic cube grids on the sphere was presented.Firstly,the gnomonic cube grids was on a two-dimensional plane by stereographic projection,then Laplace equations are solved to generate quasi-orthogonal curvilinear grids on the projection plane.Finally,the grids are transformed back to the sphere surface by the inverse of stereographic projection.The produced grid configuration has quasi-uniform cell-size on the whole sphere surface except the neighbourhood of eight major corner vertices.Moreover,another two methods which include equi-angular gnomonic projection and conformal mapping were also introduced to generate spherical grids.The resulting comparisons between three methods would be presented at last.Some quantities such as the grid length along two directions,the angle deviation from orthogonality and the area of the cell were used to evaluate the quality of the grids generated by three methods.The results show that the equi-angular gnomonic projection produces grids of the most uniform size,but are non-orthogonal,while elliptic-smoothing combined with stereographic projection method produces quasi-orthogonal curvilinear grids that are much like that of conformal mapping method.The small grid cells in the neighbourhood of eight corner vertices could be improved by stretching method,or this small defect could be circumvented by implicit time integration method,which demonstrate the kind of grid newly produced is fit to be a model grid on which the finite difference method or finite volume method can be implemented for numerical simulation of global atmosphere or ocean dynamics on large scale. Laplace equations;stereographic projection;orthogonal curvilinear grids;Neumann orthogonal boundary condition 2015-06-18; 2015-10-13 国家自然科学基金资助项目(41306078) 卢付强(1984-),男,博士,研究方向为地图学与地理信息系统。E-mail:lufuqiang2000@163.com 10.3969/j.issn.1672-0504.2016.01.004 P208 A 1672-0504(2016)01-0018-063 结果分析与比较

4 结语