基于ε-Voronoi图的矢量数据自适应简化方法

张 振 鑫,邓 浩,寇 一 丹,张 维,刘 嫔

(1.北京师范大学地理学与遥感科学学院遥感科学国家重点实验室，北京 100875；2.中南大学地球科学与信息物理学院,湖南 长沙 410083；3.中南大学信息科学与工程学院,湖南 长沙 410083)

基于ε-Voronoi图的矢量数据自适应简化方法

张 振 鑫1,邓 浩2,寇 一 丹1,张 维2,刘 嫔3

(1.北京师范大学地理学与遥感科学学院遥感科学国家重点实验室，北京 100875；2.中南大学地球科学与信息物理学院,湖南 长沙 410083；3.中南大学信息科学与工程学院,湖南 长沙 410083)

针对矢量数据简化的问题，提出一种基于帧缓存和四叉树索引的自适应简化方法，即采用四叉树索引对矢量数据进行区域划分，通过评价各个区域地物实体分布密度的指标，判断各个区域内的矢量数据密度、图幅宽度，得到各区域ε-Voronoi图中的ε值，再借助帧缓存技术，自适应地简化各个区域内的矢量数据。实验表明，该方法一定程度上提高了简化质量，为矢量数据可视化应用提供一定的基础。

四叉树；帧缓存；自适应；简化

0 引言

随着硬件平台及相关技术的发展，人们获取空间数据的能力急剧增长，甚至超出计算机存储能力的增长速度。这些数据包含大量的空间矢量数据，对矢量数据的可视化是矢量数据应用的一个重要方面[1]，矢量数据简化又是空间数据可视化研究的重要内容。

矢量数据简化研究源于Douglas与Peuker提出的Douglas-Peuker折线简化法[2],该方法效率较高，且可保持线要素的重要几何特征，但在简化过程中会导致拓扑关系发生改变，造成简化后的线要素可能出现自相交等拓扑关系不一致错误[3]。Guibas等[4]证明:在避免自相交的情况下，保留尽可能少的点是一个NP-hard问题。Estkowski[5]等在Douglas-Peuker算法的基础上，采用“绕远之路(detour)”的方式避免简化后的自相交，该算法的时间复杂度最高为O(n3)，且运行速度较慢；Yang 等[6]采用Visvalingam-Whyattt算法，并结合约束条件的限制，避免了简化后的自相交，时间复杂度为O(nlogn)，但多分辨率空间编码带有一定的冗余，影响了简化效率。文献[7，8]采用矢量数据顶点聚类的方式，即选出每个聚类中的一个点来代替每个聚类中的点，但该方法在避免简化后线段间的自相交方面仍显不足。Mustafa 等[9]提出了一种基于ε-Voronoi图的简化方法，即通过模板深度缓存，将ε-Voronoi区域渲染到模板缓存中，再通过模板测试，剔除ε-Voronoi区域外的点，保证每个要素简化结果都位于ε-Voronoi区域中，一定程度上可避免要素间的相交，但不能避免要素内部的自相交，因为每个矢量实体的ε值固定，该简化方法在灵活性和自适应性方面略有欠缺，且没有考虑待简化区域地物分布密集程度对简化的影响。Yang等[10]通过引进单调链[11]，提出了一种基于帧缓存和ε-Voronoi图的简化方法，通过剔除模板外不合规线段进行简化，一定程度上避免了简化后要素间的相交和每个要素内部的自相交，但该方法存在以下问题：1)ε值灵活性不够，导致不同分布密度的矢量数据都在相同的ε值下简化，进而导致生成ε-Voronoi图较困难，甚至一些矢量地物的ε-Voronoi图将距离较近的其他矢量实体的ε-Voronoi图完全覆盖，导致简化结果出现拓扑错误；2)借助帧缓存剔除违规线段，当待简化的矢量数据数量较多时，一些矢量数据可能映射到较少甚至几个像素中，会导致剔除违规线段时出现异常，简化结果出现拓扑错误。由于地物空间分布多样性及复杂性，亟须一种根据矢量地物分布疏密程度的自适应简化方法以提高简化质量。

本文提出一种基于帧缓存和四叉树的矢量数据自适应简化方法，通过对矢量数据建立四叉树索引，对区域进行划分，在评价每个子区域矢量数据密集程度的基础上，确定每个叶子节点区域的ε值，使每个叶子节点区域简化与该区域的矢量实体分布的密集程度相适应，提高简化质量。

1 矢量数据区域划分

通过建立矢量数据的四叉树索引进行区域划分。首先，设定四叉树叶子节点中矢量地物数目阈值，而后以每个矢量地物(polyline或polygon)的最小外包矩形(MBR)中心点为四叉树划分的基本点，进行四叉树区域划分。为更好地评价各个子区域的分布密度，需要保证每个叶子节点区域的范围一致，因此，本研究采用完全四叉树的方式进行区域划分。设每个叶子节点中实体数目的阈值为m， 矢量数据完全四叉树构建的步骤如下：1)遍历矢量数据，统计位于各个子节点矢量数据MBR中心点的数量γ。2)如果位于所有子节点矢量数据的数目γ都小于m，则完全四叉树构建完毕；反之，四叉树深度增加，各个子节点分裂成4个新的子节点，重复执行步骤1)，直到所有子节点中矢量实体的数目都小于m，四叉树构建完毕，将对应的矢量实体划归到各个四叉树叶子节点中。图1是阈值为2的完全四叉树的区域划分结果。

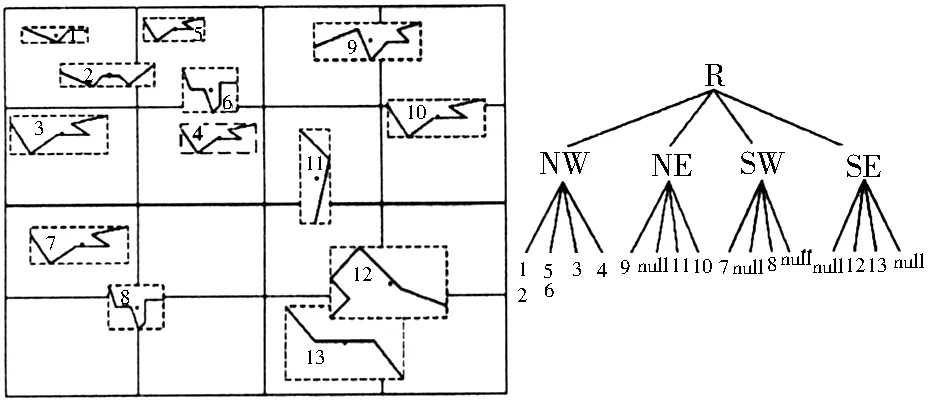
图1 矢量数据的四叉树划分

Fig.1 Dividing the vector data by Quadtree

2 基于帧缓存简化

2.1 矢量实体的εi-Voronoi图定义

εi-Voronoi图即具有距离约束条件εi的Voronoi图，每个εi-Voronoi图内的点到其矢量数据对象的最小距离不大于εi值。设矢量数据集合G是由n个矢量实体组成，即g1,g2,…,gn∈G，定义gi的εi-Voronoi图(简称εi-V(gi))为所有到gi的距离不大于εi的点的集合，即εi-V(gi)={p|dist(p,gi)≤dist(p,gj),dist(p,gi)≤εi,i≠j,j=1,2,…,n}，则G的εi-Voronoi图的集合为εi-V(G)={ε1-V(g1),ε2-V(g2),…,εn-V(gn)}，如图2所示，ε1、ε2、ε3形成3条矢量地物实体的εi-Voronoi图的集合。

2.2 自适应参数εi值的计算

本文的自适应简化方法是通过四叉树叶子区域的道路分布密度、叶子节点区域宽度和参数自适应地确定εi-Voronoi图中εi值实现的，过程如下:

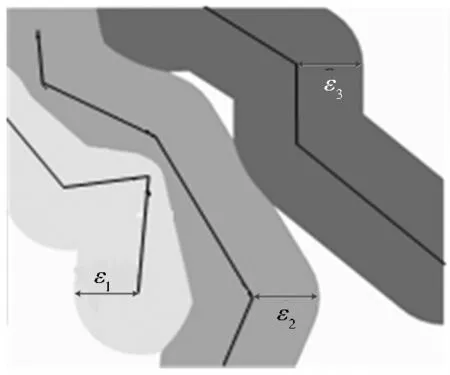
图2 εi-Voronoi图示意

Fig.2εi-Voronoi diagram

首先，设计衡量各个叶子节点区域矢量数据密度(σi)的方法：

(1)

其中:ki代表第i个叶子节点包含的所有矢量数据映射到帧缓存后各个矢量数据对应像素的数目总和；Si代表第i个叶子节点区域映射到帧缓存后该区域所覆盖的像素数目；kimax是第i个叶子节点进一步四分后(图3虚线分割后的区域)各个子区域像素数目的最大值；kimin是第i个叶子节点四分后，子区域中地物投影到帧缓存后像素数目的最小值。

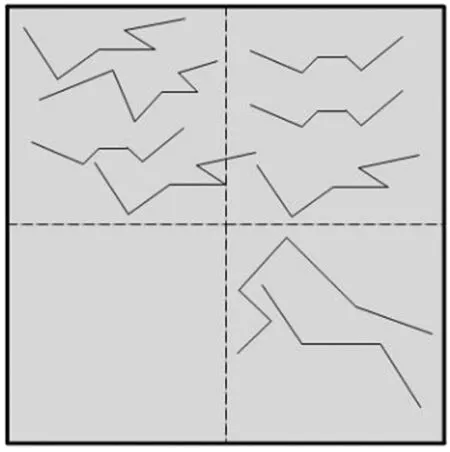
图3 叶子节点四分示意

Fig.3 Leaf nodes of the quad-tree

接着，取各个叶子节点区域密度的最大值σm,再将每个叶子节点区域的密度与σm的比值作为每个叶子节点区域的相对密度δi，即:

(2)

这样，每个叶子节点中的各矢量元素的εi值为:

εi=δi×di×α

(3)

α表示提前设定的参数，di是第i个叶子节点的图幅宽度。δi越大，表示地物越密集。图4是不同叶子节点下的矢量数据分布密度示意图。

2.3 矢量数据的简化

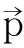
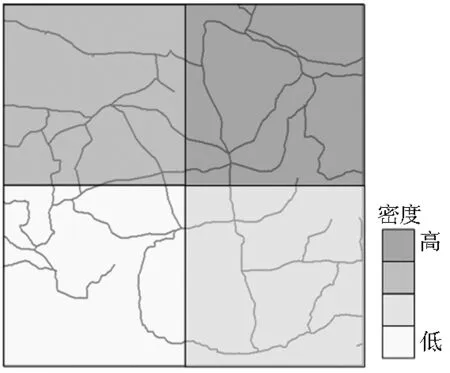
图4 叶子节点矢量地物分布密度示意

Fig.4 The density of vector data in each leaf node

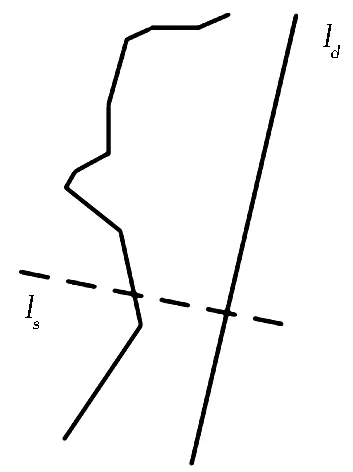
图5 单调链示意

Fig.5 Monotone chain diagram

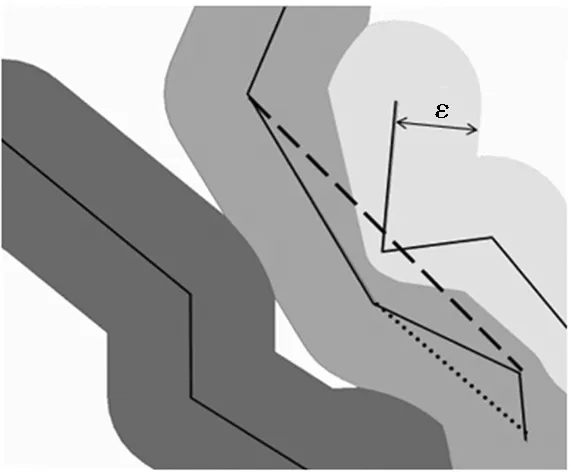
图6 εi-Voronoi图区域、合规线段(短虚线)和违规线段(长虚线)

Fig.6εi-Voronoi diagram,compliance line and irregular line

图7 线要素的简化过程

Fig.7 The procedure of line object simplification

3 实验验证与分析

3.1 数据集

表1是本研究所采用的数据集,该数据集的空间分布存在一定差异性，要素之间存在着较为复杂的拓扑几何关系。

表1 数据集

Table 1 Datesets

数据集序号名称类型要素个数节点数目1中国县级区划图polyline113336097322北京市交通图polyline155155955366

3.2 与其他方法对比

采用本文方法得到简化结果,并与文献[10]的方法进行对比(图8、图9)。本文方法的四叉树阈值设为100，α初始值设为0.005。本方法(图8b)与采用文献[10]的方法(图8c)得到的简化结果相比，更好地保持了简化前的拓扑关系，在文献[10]的方法下，一些较复杂区域的简化出现简化后相交的拓扑错误问题，本文方法可很好地保持原始数据的拓扑关系。对数据集2(图9a)，在立交桥区域，与文献[10]的方法(图9c)得到的结果相比，本文方法(图9b)能够更好地保持立交桥的原始形态特征及道路间的连通关系，得到更高质量的简化结果。

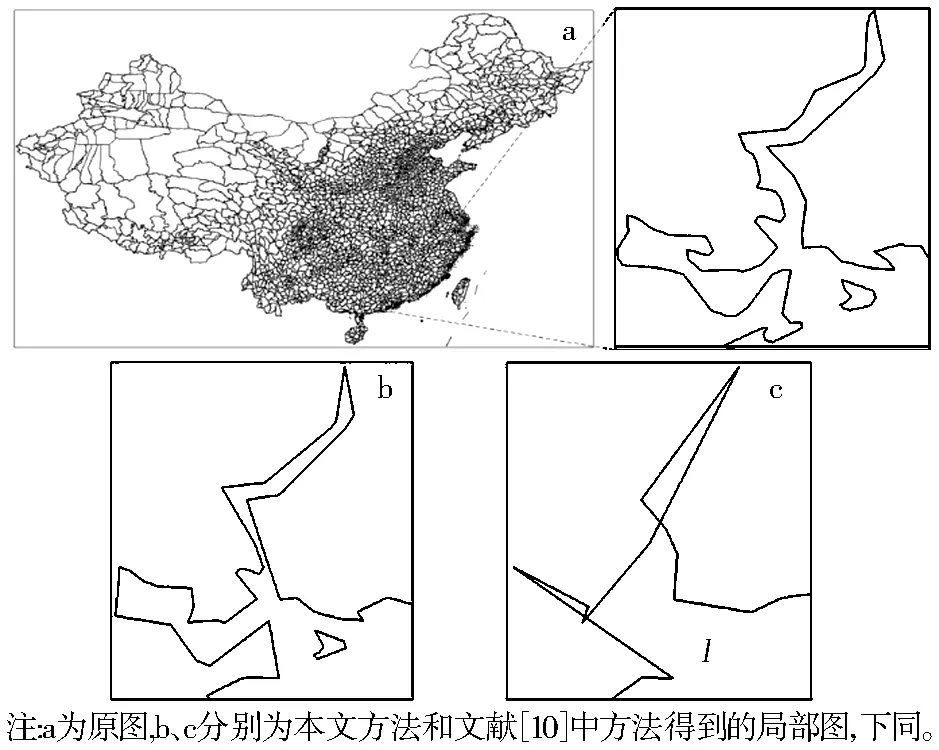
图8 数据集1的简化结果及对比

Fig.8 The result and comparison of simplification about dataset 1

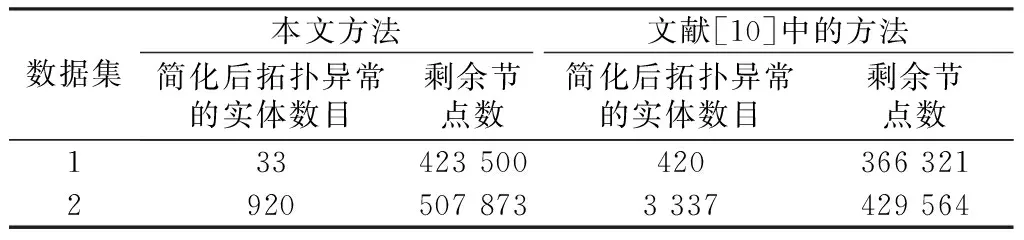
上述是从直观、可视的角度进行的对比，为了全面评价两种方法的简化结果，首先，对简化后的数据出现拓扑异常的情况进行说明，即简化后各个简化实体内部或实体间与简化前不一致，称之为异常。接着，对简化后矢量数据发生拓扑异常的实体数目和简化后的实体节点数目总和进行统计(表2)。从表2可以看出，本文方法分别对数据集1和数据集2简化后出现的拓扑异常实体数目为33和920，文献[10]的方法对数据集1和数据集2简化后出现的拓扑异常实体数目为420和3 370，本文方法在保持实体简化拓扑正确性方面有明显优势；在简化后剩余节点数方面，本文方法对数据集1和数据集2简化后的实体节点数目总和分别为423 500和507 873，而文献[10]的方法对数据集1和数据集2简化后的实体节点数目总和分别为366 321和429 564，再结合图8b和图9b可以看出，本文方法简化后保留更多节点以避免发生拓扑异常。

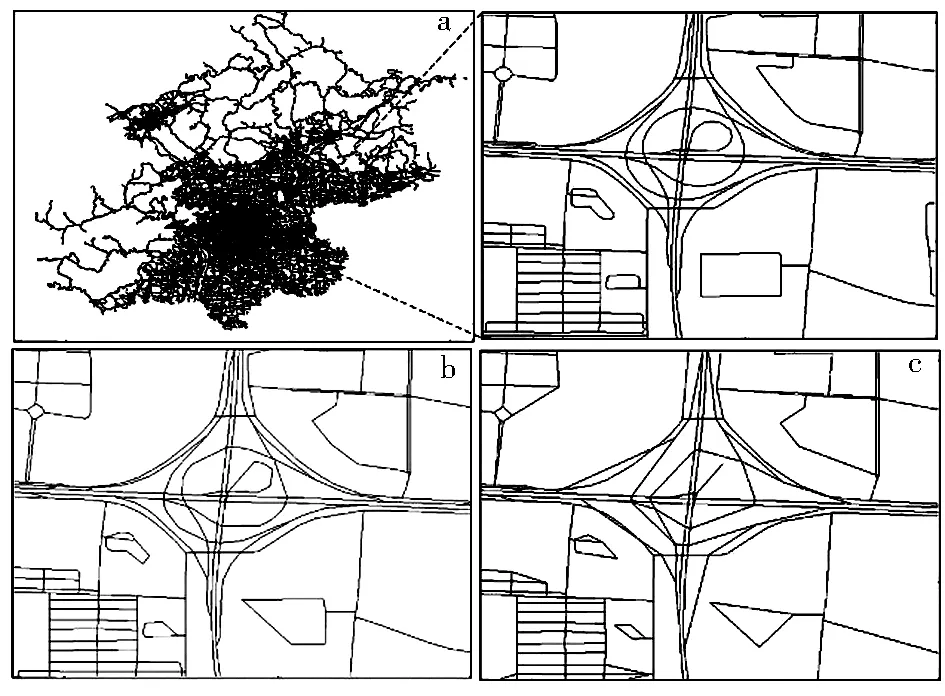
图9 数据集2的简化结果及对比

Fig.9 The result and comparison of simplification for dataset 2

表2 两种方法简化结果的统计对比

Table 2 Statistical comparison of simplification results using two methods

数据集本文方法文献[10]中的方法简化后拓扑异常的实体数目剩余节点数简化后拓扑异常的实体数目剩余节点数13342350042036632129205078733337429564

3.3 算法效率

本算法测试的硬件环境为：Intel Core i7-4770，cpu ：3.4 GHz和8 G的RAM。软件环境：操作系统为32位的Windows 7，集成开发环境是Visual C2010。对本方法的效率进行了测试，对数据集1的简化时间为143 s，数据集2的简化时间为119 s，以上测试是在单机串行的环境下进行的。

3.4 参数的敏感性测试

算法测试采用两组参数，第一组：四叉树划分阈值分别为50、100、150、200，α为0.005；第二组：四叉树划分阈值为100，α分别为0.003、0.005、0.007、0.009。本次测试以简化后矢量数据拓扑的正确率为测试标准，这里，矢量数据出现简化拓扑错误有以下几种情况：简化前数据间相交，简化后不相交；简化前数据间不相交，简化后相交；简化前数据内部不相交，简化后相交；简化前数据内部相交，简化后不相交。从图10可以看出，当四叉树索引阈值为100时，得到较高的简化正确率，说明这两套数据在四叉树索引阈值是100时，简化效果较好。从图11可得，随着α值的增大，简化后具有正确拓扑关系的矢量数据逐渐减少，这是由于随着α值增加，εi值随之增加，导致较少的线段被判断为违规线段，简化程度较大，出现简化后拓扑错误的矢量数据数目也随之增加。

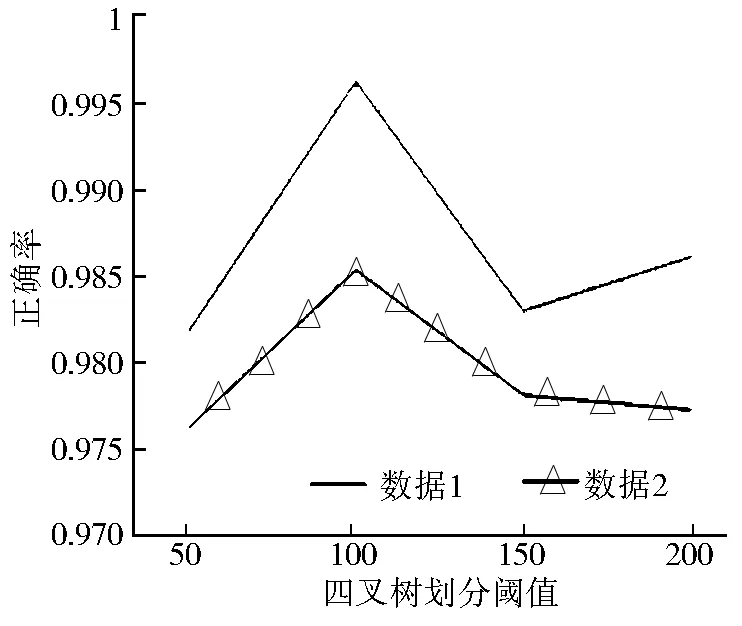
图10 不同四叉树划分阈值下的正确率测试

Fig.10 Accuracy rate test in different thresholds of Quadtree construction

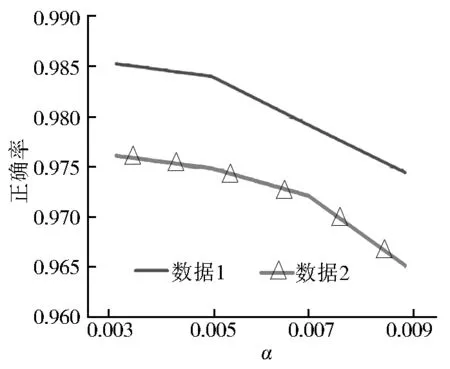
图11 不同α值下的正确率测试

Fig.11 Accuracy rate test in differentαvalue

4 结论

本研究基于矢量数据的完全四叉树索引构建子区域，提出了叶子节点子区域的数据分布密度评价指标，各个叶子节点区域根据各自的密度进行自适应简化，并通过与前人的方法对比可以看出，在简化质量上，本文方法有一定的提高，尤其是对空间分布差异较大的数据简化效果更好。后续工作将考虑采用并行方式，通过对并行简化框架的设计，将本方法进行并行化实验，进一步提高简化效率。

[1] GOODCHILD M F.Geographical information science[J].International Journal of Geographical Information Systems,1992,6(1):31-45.

[2] DOUGLAS D H,PEUCKER T K.Algorithms for the reduction of the number of points required to rep resent a digitized line or its caricature[J].The Canadian Cartographer,1973,10(2):112-122.

[3] ZHAN H S,LI G X.Progressive transmission of vector map data based on polygonal chain simp lification[J].Lecture Notes in Computer Science,2006,4282:908-917.

[4] GUIBAS L J,HERSHBERGER J,MITCHELL J,et a1．Approximating polygons and subdivisions with minimum link paths[J]．Lecture Notes in Computer Science,1993(3):383-415.

[5] ESTKOWSKI N,MITCHELL J S B.Simplifying a polygonal subdivision while keeping it simple[A].Proceedings of the 17th ACM Symposium on Computational Geometry[C].2001.40-49.

[6] YANG B,PURVES R,WEIBEL R.Efficient transmission of vector data over the Internet[J].International Journal of Geographical Information Science,2007,21(2):215-237.

[7] RAPOSO P.Scale-specific automated line simplification by vertex clustering on a hexagonal tessellation[J].Cartography and Geographic Information Science,2013,40(5):427-443.

[8] 李进,马劲松,沈婕,等.一种基于顶点聚类的线要素简化算法改进[J].测绘科学技术学报,2013,30(5):525-529.

[9] MUSTAFA N,KRISHNAN S,VARADHAN G,et al.Dynamic simplification and visualization of large maps[J].International Journal of Geographical Information Science,2006,20(3):273-302.

[10] YANG L,ZHANG L,MA J,et al.Efficient simplification of large vector maps rendered onto 3D landscapes[J].Computer Graphics and Applications,IEEE,2011,31(2):14-23.

[11] CHANDRU V,RAJAN V T,SWAMINATHAN R.Monotone pieces of chains[J].ORSA Journal on Computing,1992,4(4):439-446.

[12] HOFF III K E,KEYSER J,LIN M,et al.Fast computation of generalized Voronoi diagrams using graphics hardware[A].Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques[C].ACM Press/Addison-Wesley Publishing Co.,1999.277-286.

An Adaptive Simplification Method on Vector Data Based onε-Voronoi

ZHANG Zhen-xin1,DENG Hao2,KOU Yi-dan1,ZHANG Wei2,LIU Bin3

(1.State Key Laboratory of Remote Sensing Science,School of Geography and RS,Beijing Normal University,Beijing 100875;2.School of Geosciences and Info-Physics，Central South University，Changsha 410083;3.School of Information Science and Engineering,Central South University,Changsha 410083,China)

In this paper,an adaptive method that performs simplification of vector data using frame buffer and quad-tree index is presented.Firstly,indicators to evaluate vector data density are proposed,then the tolerance parameter (ε) ofε-Voronoi diagram is gotten by the vector data density and width of each region.In the end,the vector data is adaptively simplified with the technology of frame buffer.The result of experiment indicates that our method improves the quality of simplification quality,and provides some bases for visualization of vector data.

quad-tree;frame buffer;adaptive;simplification

2015-03-20；

2015-10-19

湖南省博士后科研资助专项计划(2014RS4028);国家自然科学基金项目(41401532)

张振鑫(1986-),男,博士研究生,从事空间信息可视化算法研究。E-mail:zhenxin066@163.com

10.3969/j.issn.1672-0504.2016.01.006

P283；P208

A

1672-0504(2016)01-0029-05