基于MPI的最小费用流网络单纯形并行算法设计与实验

吴 立 新，刘 纪 平，江 锦 成

(1.东北大学测绘遥感与数字矿山研究所，辽宁 沈阳 110819；2.中国矿业大学环境与测绘学院，江苏 徐州 221116；3.中国测绘科学研究院，北京 100830；4.北京师范大学减灾与应急管理研究院，北京 100875)

基于MPI的最小费用流网络单纯形并行算法设计与实验

吴 立 新1，2，刘 纪 平3，江 锦 成4

(1.东北大学测绘遥感与数字矿山研究所，辽宁 沈阳 110819；2.中国矿业大学环境与测绘学院，江苏 徐州 221116；3.中国测绘科学研究院，北京 100830；4.北京师范大学减灾与应急管理研究院，北京 100875)

网络最小费用流算法常用来解决资源流最优分配问题，传统的串行算法因时间复杂度高而不能满足大规模网络对计算效率的要求。该文用时间复杂度低的网络单纯形算法(NSA)的并行化求解大规模网络的最小费用流问题。通过分析NSA的可并行性，使用MPI分布式并行技术，设计了NSA并行算法；分析了3种常用流网络的拓扑结构特征及其与地理网络的关系；在并行环境下对计算效率进行实验测试，结果表明该算法具有显著的加速效果，峰值可达5.4。NSA并行算法应用面宽，可为区域及全国性大规模网络流资源分配方案的快速制定与政务决策提供有力支持。

网络最小费用流；并行计算；资源分配；网络单纯形算法(NSA)； MPI

0 引言

网络最小费用流问题旨在将交通网络上的资源以最小的总代价从供应点运输至需求点,已被广泛应用于工业生产、通讯及GIS网络分析领域，在全国性物流规划与资源调配中有着重要意义。目前，针对该问题国内外已提出了大量算法，包括消圈算法[1]、连续最短路径算法[2]、原始单纯形算法[3]等，其中，网络单纯形算法(Network Simplex Algorithm，NSA)已发展成为一种求解网络最小费用流问题的高效算法[4]。尽管NSA的时间效率不错，但因最小费用流问题本身的复杂性，串行NSA的时间复杂度依然较高。

利用高性能计算环境的硬件资源，并行技术可有效提升计算效率。通常，并行计算分为共享内存和分布内存两种模式，两者各有优缺点。目前，已有研究提出多种相关并行算法，如原始-对偶并行算法[5]、ε-松弛并行算法[6]、最小费用整型流并行算法[7]等。单纯形并行算法包括：为解决大规模线性规划问题，Yarmish等提出了基于矩阵列计算的分布式单纯形法[8]；Ploskas等在共享内存平台下实现了改进的单纯形法并行[9];其他学者则在CPU-GPUs上实现了单纯形法并行[10，11]。通常，共享内存并行受限于单机CPU数量，可扩展性差；而在分布内存并行方面，现有并行算法难以在实用中取得满意的加速效果。

为此，本文分析NSA的粗粒度可并行性，采用MPI (Message Passing Interface) 分布式并行技术对其可并行部分进行并行计算，并避免由消息传递引起并行效率低下的缺陷。旨在面向大规模计算机集群，使基于MPI的并行NSA具备高效性和强可扩展性，确保NSA并行算法适用于大规模网络最小费用流的求解。

1 网络最小费用流问题

将交通网络表达为有向图G(N,A)，包含n=|N|个节点和m=|A|条路段。任意路段(i,j)∈A包含代价cij、最大容量uij、最小容量lij和流量fij。对于节点j∈N，赋予属性bj，表示节点的供需量：bj>0表示供应量，bj<0表示需求量，bj=0表示传输节点。最小费用流问题描述如下：

最小化:

z=∑(i,j)∈Acij×fij

(1)

约束条件：

∑(i,j)∈Afij-∑(j,k)∈Afij=bj,for∀j∈N

(2)

lij≤fij≤uij,for∀(i,j)∈A

(3)

2 网络单纯形算法(NSA)

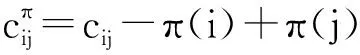
(4)

(5)

若非基态弧不满足式(4)或式(5)，则为不合格弧段。NSA包括两个阶段：1)初始解求解阶段：利用网络最大流算法[12]求得初始可行解；2)优化阶段：迭代搜索不合格弧段，并通过消圈计算，将其调整为合格弧段，操作如下：

开始

求解初始最小生成树T及B(T,L,U)；

设定T上所有节点的矢量代价π(i)；

若存在不合格弧段，则

选择不合格弧段(i,j)；

添加(i,j)至T，计算舍弃弧段(p,q)；

更新T、f和π(i)；

结束

3 分布式并行NSA

3.1 可并行性分析

本文根据并行粒度将网络进行两个层次分解，并分别并行化，实现两层次的并行计算。

(1)第一层并行。最小费用流问题是一种特殊形式的网络最大流，而最小割是最大流问题的对偶问题。根据最大流-最小割原理[12]，最小费用流的解决方案中存在一个或多个s-t割，其中s-t割C={S,T}是对节点集合N的剖分，供应点s∈S，需求点t∈T，最小割集合为{(u,v)∈A|u∈S,v∈T}。由于NSA是消圈算法的一种变种形式，最小割集上的弧段都处于饱和状态，包含割集弧段的所有回路上的最大可增广量为0，故所有穿越s-t的负值回路都是无效回路。因此，NSA能对S和T消圈计算进行并行化，且无需任何通讯代价。每个s-t割可将网络分割成两个独立子网络。因各子网络的解是完全独立的，所有子网络最优解的直接组合即为整体网络的全局最优解，无需合并后重新优化。第一层次的可并行性取决于两个因素：1)s-t割的数量：数量越多，则分割的子网络越多，可并行性越高；2)负载均衡度：S和T间的负载越均衡，并行效率越高。

(2)第二层并行。尽管NSA是一个全局优化过程，分治法[13]可将全局优化转换成局部优化。因NSA最小生成树T的根节点r的选择无特定要求，故可在第一层分割的子网络上分别进一步划分若干子区；并行构建最小生成树，对子区进行局部优化；待获得各子区的局部最优最小生成树之后，再将其合并，对合并结果执行串行NSA，得到子网络的全局最优解。理论上，假如某子网络被分割成多个大小近似的子区，则第二层并行求解的效率会很高。

3.2 基于MPI技术的并行NSA设计

(1)第一层分布式并行。首先，根据最大流-最小割原理将网络分割成多个子网络，并在这些子网络上并行执行NSA，实现第一层分布式并行，步骤如下：1)主进程根据最大流-最小割原理将网络分割成为多个子网络，表示为R0,R1,…,Ri,…；2)主进程将子网络Ri分发至从进程i；3)各从进程i执行NSA，无通讯代价地并行优化子网络Ri的局部解。

(2)第二层分布式并行化。第二层并行化是采用分治法实现子网络Ri的局部解的优化，步骤如下：1)进程i将子网络Ri进一步分割成多个子区Rij，并将子区分发给空闲从进程；2)空闲从进程j在子区Rij上执行串行NSA，获得Rij的局部最优解；3)进程i回收所有子区Rij及其局部最优解，并将所有子区合并为子网络Ri，所有子区局部最优解合并为Ri的解；4)进程i在Ri上执行串行NSA，将Ri的解优化为全局最优解。

图1为基于MPI技术的NSA并行主流程，主要包括3部分：1)网络预处理：将整个网络进行两个层次的分割，第一层根据最大流-最小割原理，将网络分割成为多个子网络，第二层遵循负载均衡原理将得到的子网络进一步分割成多个子区，并将子区数据分发至各从进程；2)子区并行求解：各从进程独立、并行地对各子区执行串行NSA，得到所有子区的局部最优解；3)子区解合并再优化：主进程收集所有从进程的子区及其局部最优解结果，合并后执行串行NSA进行再优化，得到子网络及其全局最优解,然后将各子网络的最优解写入同一结果文件，即为整体网络的全局最优解。

4 并行NSA实验测试

4.1 实验设计

本实验采用3种广泛应用于网络流算法测试的经典拓扑网络[14]：Goto网络包含2 000个节点和317 000条边；Gridgen网络包含10 000个节点和1 240 000条边；Netgen网络包含5 000个节点以及40 000条边。这些网络是1991年在Rutgers大学举办的第一次DIMACS会议上公布的[14]。其中，Gridgen随机网络生成器由Lee[15]用C语言编写，该生成器产生格网状的网络和一个超级节点，其拓扑结构与城市交通网络相近(如北京市交通网络)，生成器参数如图2所示。

Netgen网络生成器用以产生网络最小费用流问题实例[16]，可用于研究任务指派等交通网络问题[17]，其生成器参数如图3。Goto(Grid on Torus)网络有意产生特殊而困难的实例[18]，如其名所言，其基本网络结构为网状多环，与城市道路网络相匹配。每个Goto网络供应点和需求点间的供需量取决于弧段容量[19]，参数描述如图4。

实验测试环境为两台图形工作站(2.00 GHz的CPU，32核，48 GB内存)、64位Windows 7操作系统。代码设计采用C语言，使用GCC编译器编译，使用O2优化。串行算法和并行算法同在此环境下进行测试对比。相对于串行算法，并行算法的加速比speedup=ts/tp，其中ts和tp分别为串行和并行算法的计算耗时。

4.2 实验结果与讨论

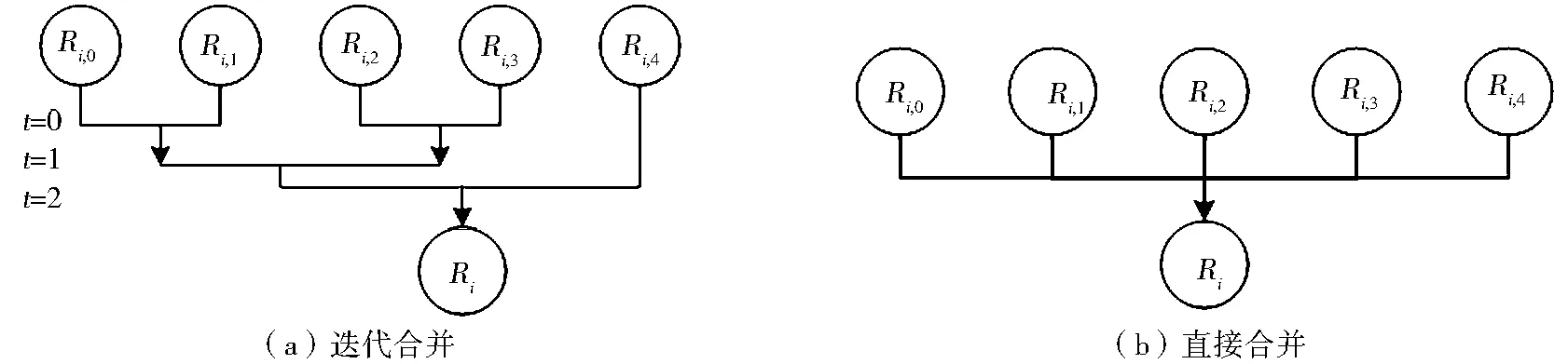
为更好地测试本文并行算法的适应性，针对第二层分布式并行中第三步的子区合并问题，本实验采用两种合并策略进行比较：迭代合并策略和直接合并策略(图5)。迭代合并策略为：在任意迭代次数t时，第2j

图1 基于MPI的并行NSA流程 图4 Goto随机网络生成器参数

Fig.1 The flowchart of MPI-based parallel NSA Fig.4 Input parameters of Goto network generator(https://lemon.cs.elte.hu/trac/lemon/wiki/MinCostFlowData)

图5 子区合并策略

Fig.5 Two strategies of merging sub-regions

不同合并策略得到不同的并行效率(图6)。在Gridgen和Netgen网络中，两种合并策略均在两个进程时取得最大加速比。显然，对比于串行算法，多个进程的计算效率始终大于单进程，迭代合并策略的最大加速比为1.6；直接合并策略的最大加速比可达5.4。然而，进程数越多，由此引发的通讯代价也越高。与Gridgen和Netgen网络不同的是，并行NSA在Goto网络中，两个进程取得较好加速比之后，随进程增加，时间效率并未立即下降，而是保持平稳或者持续轻微地增加。总之，针对以上3种网络，并行NSA的加速比都比较明显。通常，网络流算法为全局优化过程，各操作之间的关联较大，并行难度较高；但是，本文算法的并行效果明显，可达到预期目标。

图6b中出现了超线性加速比。当进程数为2时，理论上最大加速比不应超过2，实际上却达到了5.4。这是因为，串行算法最小生成树T中的弧段及节点集合的总数比并行算法最小生成树子集中的多得多，若并行算法迭代次数总和并未远超串行算法的迭代次数，就可能出现超线性加速比。

图6 并行NSA加速比

Fig.6 The speedups of parallel NSA

5 结论

本文基于MPI分布式并行技术，提出了网络并行NSA。在3种经典流网络上的测试结果表明,并行NSA相比于串行NSA的加速效果明显，峰值可达5.4。并行NSA中的迭代合并与直接合并策略具有不同的加速效果，在Gridgen和Netgen网络中两者均在两个进程时取得最佳加速比；而在Goto网络中，4个进程的加速效果较两个进程还有少量增加。总体而言，直接合并策略的加速效果比迭代合并策略明显，且出现了“超线性”加速比现象。

本文提出的并行NSA有效解决了大规模网络最小费用流的高效求解问题，可为国家政务、交通、军事及应急GIS大规模网络中的最优流资源分配方案制定提供关键技术与决策支持;提出的两种并行策略及其加速效果，也可为其他网络流算法的并行化设计提供参考。

[1] GOLDBERG A V,TARJAN R E.Finding minimum-cost circulations by canceling negative cycles[J].Journal of the ACM,1989,36(4):873-886.

[2] GOLDBERG A V,TARJAN R E.Solving minimum cost flow problem by successive approximation[A].Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing[C].ACM,1987(7)-18.

[3] GOLDFARB D,HAO J X.A primal simplex algorithm that solves the maximum flow problem in at mostnmpivots and O(n2m) time[J].Mathematical Programming,1990,47(1-3):353-365.

[4] ORLIN J B.A polynomial time primal network simplex algorithm for minimum cost flows[J].Mathematical Programming,1997,78(2):109-129.

[5] BERTSEKAS D P,CASTANON D A.Parallel primal-dual methods for the minimum cost flow problem[J]. Computational Optimization and Applications,1993,2(4):317-336.

[6] BERALDI P,GUERRIERO F.A parallel asynchronous implementation of the ε-relaxation method for the linear minimum cost flow problem[J].Parallel Computing,1997,23(8):1021-1044.

[7] ANDRZEJ L,MIA P.A fast parallel algorithm for minimum-cost small integral flows[A].Euro-Par Parallel Processing[C].Springer Berlin Heidelberg,2012.688-699.

[8] YARMISH G,SLYKE R.A distributed,scaleable simplex method[J].The Journal of Supercomputing,2009,49(3):373-381.

[9] PLOSKAS N,SAMARAS N,MARGARITIS K.A parallel implementation of the revised simplex algorithm using OpenMP:Some preliminary results[A].Optimization Theory,Decision Making,and Operational Research Applications[C].Springer Proceedings in Mathematics & Statistics,2013,31:163-175.

[10] LALAMI M E,BOYER V,EL-BAZ D.Efficient implementation of the simplex method on a CPU-GPU system[A].Proc.of the 2011 IEEE Int.Symposium on Parallel and Distributed Processing Workshops and PhD Forum[C].Washington DC,2011.1999-2006.

[11] BIELING J,PESCHLOW P,MARTINI P.An efficient GPU implementation of the revised simplex method[A].Proc.of the 24th IEEE Int.Parallel and Distributed Processing Symposium[C].2010.1-8.

[12] GOLDBERG A V,TARJAN R E.A new approach to the maximum flow problem[J].Journal of the ACM,1988,35(4):921-940.

[13] CORMEN T H,et al.Introduction to Algorithms[M].Cambridge:MIT Press,2001.

[14] BADICS T,BOROS E,CEPEK O.Implementing a new maximum flow algorithm[A].JOHNSON D S,MCGEOCH C C.Network Flows and Matching:1st DIMACS Implementation Challenge,DIMACS Series in Discrete Mathematics and Theoretical Computer Science[C].American Math.Society,1993.

[15] LEE Y.Computational Analysis of Network Optimization Algorithms[D].M.I.T,1993.

[16] KLINGMAN D,NAPIER A,STUTZ J.NETGEN:A program for generating large scale capacitated assignment,transportation,and minimum cost flow networks[J].Management Science,1974,20(5):814-821.

[17] GEORGIOS G.A Dual Network Exterior Point Simplex-Type Algorithm for the Minimum Cost Network Flow Problem[D].Geranis,Georgios,2012.

[18] GOLDBERG A V,KHARITONOV M.On implementing scaling push-relabel algorithms for the minimum-cost flow problem[A].DIMACS Series in Discrete Mathematics and Theoretical Computer Science[C].1993,12:157-198.

[19] KOVCS P.Minimum-cost flow algorithms:An experimental evaluation[J].Optimization Methods and Software,2015,30(1):94-127.

Design and Experiment on MPI-Based Parallel Network Simplex Algorithm for Network Minimum-Cost Flow

WU Li-xin1,2,LIU Ji-ping3,JIANG Jin-cheng4

(1．Institute of Geo-informatics & Digital Mine,Northeastern University,Shenyang 110819；2.School of Environment Science & Spatial Information,China University of Mining and Technology,Xuzhou 221116;3.Chinese Academy of Surveying & Mapping,Beijing 100830;4.Academy of Disaster Reduction and Emergency Management,Beijing Normal University,Beijing 100875,China)

Network minimum-cost flow algorithms are usually used to solve optimal flow resource allocation problems.However,the traditional sequential algorithm is not efficient enough to satisfy the requirement of computing performance in large-scale network due to its high time-complexity.With the rapid development of computer technology,parallel computing is becoming an effective way of solving the computational bottleneck.This paper utilizes the relatively low time-complexity network simplex algorithm (NSA) to solve the network minimum-cost flow problem,and designs the parallel computing process of NSA.Analyzing to the parallelizability of NSA,distributed parallel NSA using MPI (Message Passing Interface) technology is designed for high-performance computing platform.The topological structures of three types of classical flow networks are discussed and referred to that of geographical networks.Experimental tests on the three classical flow networks demonstrate that the proposed parallel NSA displays notable acceleration effect,and the maximum speedup reaches 5.4.The proposed parallel NSA provides powerful support for rapid solution of large network resource allocation and decision making on national affairs at regional or national scale.

network minimum-cost flow;parallel computing;resource allocation;network simplex algorithm(NSA);MPI

2015-09-25

国家863计划项目(2011AA20302)；测绘地理信息公益性行业科研专项经费项目(201512032)

吴立新(1966-)，男，教授，博导，长江学者特聘教授，国家杰出青年基金获得者，主要研究方向为：空间信息理论与算法、灾害遥感与协同观测。E-mail：awulixin@263.net

10.3969/j.issn.1672-0504.2016.01.001

P208;TP301.6

A

1672-0504(2016)01-0001-05