砂性土边坡冲刷量计算及试验研究
李 芬 吴福宝 武江涛
(武汉理工大学交通学院1) 武汉 430063) (中铁第四勘察设计院集团有限公司2) 武汉 430063)
砂性土边坡冲刷量计算及试验研究
李芬1)吴福宝2)武江涛1)
(武汉理工大学交通学院1)武汉430063)(中铁第四勘察设计院集团有限公司2)武汉430063)
摘要:针对目前对砂性土边坡冲刷破坏研究的不足,对基于能量法的路堤边坡冲刷量公式进行了修改,使其可应用于砂性土路堑边坡冲刷量计算,结合室内边坡冲刷模型试验,对计算公式的合理性进行了验证,并根据试验现象得到坡面冲刷破坏的一般规律.研究结果表明,修改后的冲刷量公式在计算砂性土边坡冲刷量时具有较好的准确性.
关键词:能量法;砂性土;冲刷量;模型试验
0引言
降雨是边坡发生破坏的主要诱因.持续的强降雨,可引起边坡坡面的冲刷破坏,更为甚者可发生坡体的滑塌和泥石流.这将会对人民的人身安全造成严重威胁,经济财产造成巨大损失,所以对边坡冲刷破坏的机理研究具有重要的理论价值和工程意义.
近年来国内外学者对边坡冲刷破坏机理的研究逐渐增多,但这些研究结果相差较大,其主要原因在于影响边坡冲刷量的因素较多,且各个影响因素与边坡冲刷量之间的关系还不很明确.在计算边坡冲刷量时,柴国辉等[1]利用河流泥沙运动力学中的坡面流挟砂量对施工期的边坡冲刷量进行分析;国内一些学者采用将现场观测数据建立神经网络来对冲刷量进行预测[2-5],但当数据较少或较为片面时,这种方法将对计算结果的准确性造成很大影响;曹文洪[6]在对土壤侵蚀的坡度界限研究中,应用泥沙运动力学和水力学原理对在降雨情况下的边坡冲刷机理做出了初步的理论分析;李志刚[7]首先把能量法应用于路基边坡冲刷临界坡度的研究;刘建民[8]在文献[7]的基础上对路基边坡的冲刷量做了进一步的研究,获得了相应的计算公式.本文基于前人对冲刷量研究的基础上,对冲刷量计算公式进行了一定修改,使其可应用于砂性土路堑边坡,并结合室内冲刷试验结果进行验证,找出砂性土边坡冲刷的一般规律和冲刷量的合理计算公式.
1砂性土边坡冲刷量公式推导
1.1坡面水流水力学参数计算
对边坡冲刷机理研究时,假设在径流达到平衡的坡长为L,此时水流的冲刷能力最强,坡面水流的模拟见图1.由泥沙运动力学和曼宁公式可得坡长L处的水深h和流速vL.

图1 坡面水流分析
坡长L处的水深h为
(1)
式中:I为降雨强度;λ为砂土入渗率;θ为边坡坡度;n为曼宁系数.
坡长L处水流流速vL为
(2)
进而可计算坡脚处的单宽流量:

(3)
坡面汇水时间的一般公式为
(4)
1.2能量法公式推导
对土的水力冲刷而言,各因子的作用可通过对冲刷能量的分配和转换来描述.能量分配和转换服从能量平衡原理,各因子的能量效应服从能量叠加原理,所以冲刷过程能量分配和转换也服从能量守恒和转换定律.
通过分析水流从坡顶流至坡脚过程中的物质变动和能量收支,可建立土体冲刷能量平衡方程为
E0+E1=E2+E3
式中:E0为水土流微元在坡顶的势能;E1为水土流微元在坡顶的初始动能;E2为水土流微元流经坡面时的摩擦耗能;E3为水土流微元流至坡脚时的动能.
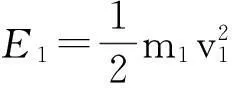
现得到路堑边坡冲刷能量平衡方程:
(5)
式中:m1为水土流微元初始质量(此时仅为水流质量);m2为水土流变化量;v2为水土流在坡脚的速度,即v2=vL.
进而得
(6)
由于m2=Δm+ΔQ⟹Δm=m2-qt0.式中:Δm为泥沙增加量;ΔQ为水的增加量.
则,
Δm=m2-qt0=
(7)
坡面上的汇水量近似等于坡脚处的总流量,即

(8)
式中:ρ为水的密度;B为坡面宽度;t为降雨时间.
单宽面积上的水流微元初始质量为
(9)
则路堑边坡总冲刷量表达式为
(10)
2室内冲刷试验设计
2.1试验装置
结合实际砂土边坡工况,对模型试验装置进行设计.冲刷试验模型箱采用透明有机玻璃制作,其长宽高尺寸分别为1.9 m×0.5 m×1.3 m,箱底钻有若干圆孔;为模拟透水边界条件,试验箱底部垫一层约5 cm厚的碎石垫层,碎石垫层上铺盖土工布,保证在降雨入渗过程中水能从底部很快排出.所选试验用砂均过0.5 mm筛,去除杂质,试验用砂的渗透系数为331 mm/h,平均粒径约0.25 mm.降雨装置采用直径16 mm PVC管间隔钻孔制作,长宽尺寸为140 cm×50 cm,孔间间距为4 cm,钻孔直径为0.8 mm,为保证降雨均匀,管间间距也设计成4 cm,见图2.降雨强度按水表流量除以总降雨面积及总降雨时间计算.

图2 实验模型箱及降雨装置
2.2试验方案设计
为消除其他影响因素的影响,各组冲刷试验均采用1∶1.5坡比,坡体堆砌时需分层压实.冲刷历时以坡面开始产生径流后持续冲刷5 min.试验结束后,将冲到坡脚以外的泥沙收集,烘干称重.考虑不同坡高和降雨强度对边坡冲刷量的影响,冲刷模型设计方案具体实施为:当雨强(450 mm/h)固定不变时,模型边坡坡高分别采用0.4,0.6和0.9 m,依次记录这3种不同坡高下的冲刷量结果;当坡高(0.9m)固定不变时,冲刷模型雨强分别采用457,545和633 mm/h,记录这3种不同雨强下的冲刷量结果.
3试验冲刷结果及理论分析
刚开始降雨时,坡面砂土尚未饱和.雨滴从高处落到坡面,具有一定的动能,对坡面表层结构造成破坏,出现很多溅蚀坑,在试验前期可看到,很多泥沙被击溅到两边的玻璃壁上,该阶段被称为雨滴溅蚀.随着降雨的继续,坡面表层泥沙逐渐接近饱和,当某一区域雨强超过砂土的入渗率时,坡面便开始形成少量积水,薄层积水在重力的作用下,开始向下流动,坡面出现一片片鳞状凹坑,该阶段称为片蚀现象,见图3.随着时间的推移,坡面的积水逐渐增多,在重力的作用下,雨水将自上而下汇集,在坡面上形成一条条浅沟,坡面径流(见图4)现象开始出现,该阶段称为沟蚀现象.随着汇水量的增大,细沟将开始横向发展,不断加深,沟槽内部泥沙不断被雨水带走,沟槽上部泥沙逐渐失去平衡,发生局部坍塌,至此坡面侵蚀破坏过程结束.

图3 雨滴溅蚀

图4 坡面径流
试验结束后,将冲到坡脚以外的泥沙烘干称重.测得不同坡高情况下的边坡冲刷量分别为33 636,48 976和78 529 g;不同雨强情况下的边坡冲刷量分别为78 529,156 945和220 685 g.从2组数据可看出,当其他因素固定不变时,边坡的冲刷量会随着坡高或雨强的增大而增大,坡高和雨强2个影响因素均与冲刷量成正比关系.
3.2理论计算及冲刷试验结果对比
根据室内模型试验条件,对雨强、坡型和冲刷历时等参数进行合理选取,将这些参数带入式(10)中,得到不同雨强或不同坡高设计方案下的砂性土冲刷量理论结果,见图5.

图5 理论值与试验值结果对比
由图5可见,相同条件下的试验值和理论值较吻合,其误差最大约20%,表明式(10)在预测砂性土边坡冲刷量时具有良好的效果.此外,根据砂性土边坡冲刷量的试验值和理论计算值,可对雨强和坡高2个影响因素进行敏感性分析,得到雨强对边坡冲刷量影响的比例系数,其中试验值为7.10,理论值为5.45;坡高对边坡冲刷量影响的比例系数为试验值2.24,理论值2.25.因此雨强对砂性土边坡冲刷量的影响要比坡高对砂性土边坡冲刷量的影响更为明显,两者相差约3倍关系.
4结论
1) 结合实际工点选用细砂土为研究对象,考虑到其粒径较小且整体分布均匀,与弹性力学中理论假设相近,符合冲刷量理论计算时推导条件,根据能量法对坡面冲刷量公式进行了推导,并设计相关模型试验,使得试验结果与理论计算值之间具有可比性,为下一步的理论验证奠定基础.
2) 根据边坡冲刷量的试验值和理论值结果对比,可看出修改后的冲刷量公式在砂性土边坡冲刷量计算时与试验结果具有较好的吻合性,可将其应用于实际工程冲刷量预测中.
3) 当其他影响因素不变时,边坡的冲刷量会随着坡高或雨强的增大而增大,坡高和雨强两个影响因素均与冲刷量成正比关系;此外,雨强对砂性土边坡冲刷量的影响要比坡高对砂性土边坡冲刷量的影响更为明显.
参 考 文 献
[1]柴国辉,柴旺.公路边坡施工期坡面冲刷量分析[J].公路交通技术,2010(1):6-7,11.
[2]姜仁安,郭梅,任忠.神经网络在边坡土冲刷量计算中的应用[J].公路交通科技:应用技术版,2007(12):59-60,66.
[3]李凯,王昌贤,杨兴武.边坡冲刷量的神经网络计算模型[J].交通科技与经济,2009(6):77-79.
[4]李志刚.基于神经网络的公路边坡冲刷量模拟计算[J].东南大学学报,2002,32(6):961-963.
[5]王春辉.基于MATLAB神经网络工具箱的边坡冲刷量计算[J].解放军理工大学学报,2003,4(5):75-77.
[6]曹文洪.土壤侵蚀的坡度界限研究[J].水土保持通报,1993,13(4):1-5.
[7]李志刚.基于能量法的高等级公路路堤边坡冲刷临界坡度研究[J].东南大学学报,2003,33(3):340-342.
[8]刘建民.基于能量法的路堤边坡冲刷量计算模型研究[J].中国公路学报,2004,17(4):22-24.
Erosion Quantity Calculation and Experimental Study of Sandy Slope
LI Fen1)WU Fubao2)WU Jiangtao1)
(SchoolofTransportation,WuhanUniversityofTechology,Wuhan430063,China)1)
(ChinaRailwaySIYUANSurveyandDesignGroupCo.,Ltd.,Wuhan430063,China)2)
Abstract:As the current research on the erosion failure of sandy slope contains deficiency, this paper modifies the energy based calculation formula for embankment slope erosion to enable it to calculate the erosion quantity of sandy cutting slope. By conducting laboratory model test of slop erosion, the modified formula is verified and the general laws of slope erosion are obtained. The study shows that the modified formula has good accuracy in the calculation of the erosion quantity of sandy slope.
Key words:energy method; sandy slope; erosion quantity; physical model test
doi:10.3963/j.issn.2095-3844.2016.02.018
中图法分类号:U416.1
收稿日期:2016-01-12
李芬(1974- ):女,博士,副教授,主要研究领域为岩土工程

