基于级联广义逆法的动力定位推力分配*

徐海祥　付海军　殷进军　龙　飞

(高性能船舶技术教育部重点实验室1)　武汉　430063)　(武汉理工大学交通学院2)　武汉　430063)

(武汉船用电力推进装置研究所3)　武汉　430063)



基于级联广义逆法的动力定位推力分配*

徐海祥1,2)付海军2)殷进军3)龙飞3)

(高性能船舶技术教育部重点实验室1)武汉430063)(武汉理工大学交通学院2)武汉430063)

(武汉船用电力推进装置研究所3)武汉430063)

摘要：针对一般广义逆算法直接求解动力定位推力分配问题存在推力和角度饱和的现象，采用了级联广义逆算法求解动力定位推力分配问题.该算法通过对饱和推力与饱和角度进行截断处理, 保证了优化问题的解在可行域内.仿真结果表明，该算法能有效避免推力分配中出现的推力与角度饱和现象.

关键词：动力定位；推力分配；饱和处理；级联广义逆

0引言

动力定位技术作为传统锚泊定位方式的替代被广泛应用于深水钻探、海底管线铺设与检修、水下机器人、平台供应等工程作业中.推力分配作为动力定位的重要技术环节，其任务是在要求的控制周期内迅速给出各推进器的推力与方向以满足上层控制器所要求的待分配力和力矩.为保证定位作业所要求的操纵性和可靠性，具有动力定位功能的船舶一般为过驱动系统，这也使得推力分配成为一个优化问题[1].

目前，应用于求解推力分配问题的算法主要包括直接分配[2]、二次规划[3]、广义逆[4-5]、乘子法[6]等算法，其中广义逆算法以其原理简单、实时性好而被广泛用于过驱动航天器、飞机、船舶等的受限控制分配[7].但采用一般广义逆算法直接求解推力分配问题存在推力和角度饱和的现象.O.J.Sørdalen采用奇异值分解法以解决推进器饱和问题，并提出了扩展推力的概念；施小成等采用级联广义逆算法研究了固定角度模式下的推力分配问题，并对推进器推力饱和问题进行了探讨，但未考虑推进器角度饱和问题.

本文针对全回转推进器在进行推力分配时可能同时存在推力饱和和角度饱和的问题，采用级联广义逆算法对其饱和推力与饱和角度进行截断处理.为验证算法的有效性，对一艘装备有全回转推进器的动力定位船模进行了仿真实验.

1推力分配问题

建立如图1所示的船体坐标系：原点位于船中，以船舶纵向为x轴，横向为y轴.

图1　船体坐标系

对配备有n个推进器的动力定位船舶，假设其中有r个全回转推进器；n-r个槽道推进器.u=(u1,u2,…,ui,…,un)为推进器发出的推力，其中：ui为第i个推进器的推力.引入扩展推力将全回转推进器推力ui沿坐标轴分解为uix，uiy.

图2为全回转推进器推力分解.由图2可见，第i个全回转推进器的角度可由式(1)得出.

图2　全回转推进器推力分解

(1)

推力分配目标函数可表示为

minf=uTWu

(2)

式中：W为权值矩阵，W∈R(n+r)×(n+r).

动力定位船舶满足定位作业要求即是使得推进器执行机构在船舶水平面内3个自由度上产生的力和力矩等于上层控制器所要求的待分配力和力矩.建立水平面内3个自由度上的平衡方程.

(3)

式中：τc=[τx,τy,τm]为待分配力和力矩;

其中，(lxi,lyi)为第i个推进器的安装位置.

综上，推力优化分配问题可表达为

(4)

采用拉格朗日乘子法将上述问题转化为无约束最优化问题.

(5)

式中：λ∈R3为拉格朗日乘子.依据卡罗儒-库恩-塔克(KKT)条件，函数在极值点满足：

(6)

(7)

由式(6)和式(7)可得：

(8)

综合式(6)～(8)可得满足平衡方程的推进器推力为

(9)

即当矩阵BW-1BT可逆时，式(4)解可由式(9)给出.

当W取单位矩阵时，式(9)简化为

(10)

在实际工程中，由于推进器的物理限制也即在第j个控制周期内要求推进器推力和角度满足：

(11)

式中：ujmin=max(umin,uj-1-Δu)

ujmax=min(umax,uj-1+Δu)

αjmin=αj-1-Δα

αjmax=αj-1+Δα

(12)

其中：Δα，Δu分别为推进器角度变化率和推力变化率；umax，umin分别为推进器最大推力和最小推力；αjmax，αjmin，ujmax，ujmin分别为j时刻推进器角度上、下限和推力上、下限.

在使用一般广义逆算法求解推力分配问题时，仅仅考虑了等式约束，由于推进器的上述物理限制如推力极限、推力变化率、角度变化率等，推进器无法转到所要求的角度或发出所要求的推力.如果对该问题不加处理将导致无法满足上层控制器所要求的待分配力与力矩.

2级联广义逆算法与饱和处理

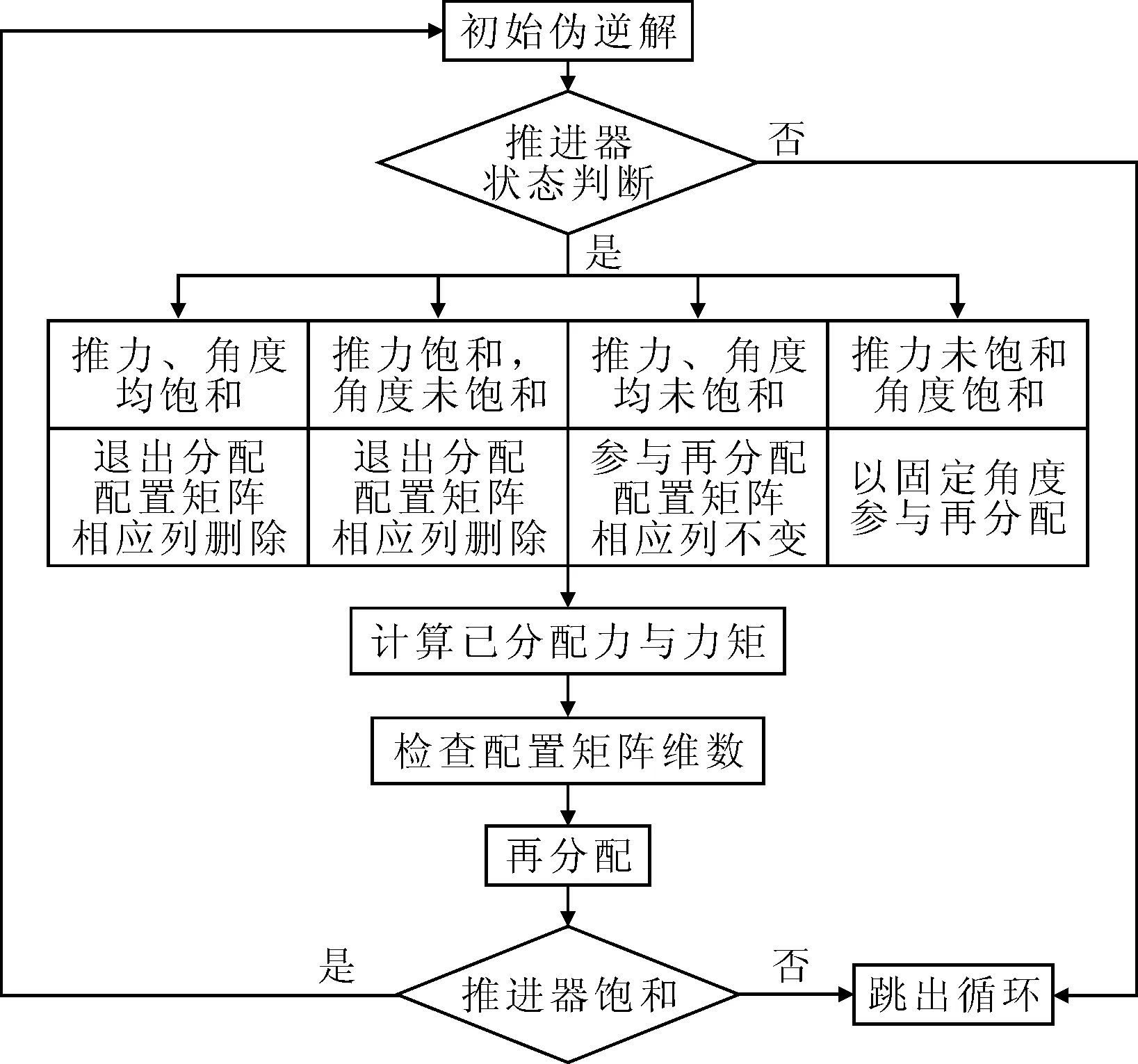
为了解决一般广义逆算法求解推力分配问题时出现的饱和现象，本文采用了级联广义逆算法，该算法具体描述如下.

首先由式(10)得到初始解，并由式(1)计算全回转推进器的角度.根据式(11)判断推进器是否饱和.这里，根据推进器是否饱和将推进器状态分为4类：(1)推进器推力饱和，推进器角度未饱和；(2)推进器推力未饱和，推进器角度饱和；(3)推进器推力和推进器角度均饱和；(4)推进器推力和推进器角度均未饱和.

针对上述4种情况,本文采用以下4种相应处理办法.

1) 饱和推力截断处理，将配置矩阵中对应的列移除，退出分配.

2) 饱和角度截断处理，将推进器固定在饱和角度处，以定轴推进器参与再分配，配置矩阵对应列变为[cosαi0,sinαi0,-lyicosαi0+lxisinαi0]T，αi0为推进器角度上限或下限.

3) 饱和推力与饱和角度截断处理，将配置矩阵对应列移除，退出分配.

4) 参与再分配，配置矩阵对应列不变.

特别需要指出的是：根据推进器饱和状态进行配置矩阵重构时，如果配置矩阵非零列少于3列，那么式(10)不再适用.这是因为对于矩阵Am×n，只有当m

(13)

采用级联广义逆算法解决推进器饱和问题流程见图3.

图3　级联广义逆饱和处理流程

3仿真结果与分析

3.1仿真实验参数

为验证该算法的有效性，本文对一艘配有动力定位系统的船模进行了推力分配的仿真实验.推进器布置见图1，推进器相关技术参数见表1.

表1　推进器技术参数

3.2仿真结果与分析

仿真结果见图4～9.图中GI，CGI分别为采用一般广义逆算法、级联广义逆算法的求解结果.以图4中对1号推进器的角度饱和处理为例：图中的局部放大图显示在采用一般广义逆算法计算得到的1号推进器角度变化较为剧烈，超出了推进器角度变化率的限制，推进系统无法执行，这将导致实际输出力与力矩和待分配力与力矩存在偏差.采用级联广义逆算法时，当1号推进器的角度超出推进器角度下限时进行截断.由图中可看到：在30～40 s仿真周期内，经饱和处理后推进器角度变化平缓且在合理区域内，有效解决了全回转推进器的角度饱和问题.

图4　1号全回转角度变化曲线

图5　2号全回转角度变化曲线

图6　1号全回转推力变化曲线

图7　2号全回转推力变化曲线

图8　1号侧推推力变化曲线

图9　2号侧推推力变化曲线

图6中在30，70 s仿真周期及图7中40 s仿真周期附近，由GI得的全回推进器扩展推力计算得到全回转推进器角度不满足不等式约束，经对推进器饱和角度截断处理后，等式约束无法满足.若该全回转推进器推力未饱和则将该全回转推进器的方位角固定在角度上(下)限处以定轴推进器的形式参与重分配.在重新分配过程中出现全回转推进器发出负力的情况，由于设置全回转推进器不能发出负力，因而对负推力作了截断处理使该全回转推进器发出零推力，这说明了饱和处理的有效性，保证推进器推力在可行范围内.

由图6～9可见，由CGI所得的推进器推力峰值较GI所得的推进器推力峰值要大.这是由于采用GI时没有考虑推进器角度变化率的限制，推进器总能朝着最有利(能耗最优)的方向发力，以相对较小的推力就能满足平衡方程.采用CGI时，考虑到推进器角度变化率的限制，对推进器饱和角度截断处理后，全回转推进器并不是朝着最有利的发力方向，推进器需要发出更大的推力才能满足平衡方程.

5结 束 语

文中采用级联广义逆算法根据推进器的饱和状态类型进行配置矩阵重构，对饱和推力、饱和角度进行截断处理后经重新分配以满足上层控制器所要求的待分配力与力矩.在给定同一组待分配力和力矩的条件下，通过2组仿真实验比较饱和处理前、后的结果，仿真结果表明：虽然能耗会有所增大但该算法能有效解决全回转推进器的推力饱和和角度饱和问题.

参 考 文 献

[1]边信黔,付明玉,王元慧.船舶动力定位[M].北京:科学出版社,2011.

[2]SHENGYONG T, ZHANG S, ZHANG Y.A modified direct allocation algorithm with application to redundant actuators[J]. Chinese Journal of Aeronautics,2011,24(3):299-308.

[3]MARTIN R. Fuel optimal thrust allocation in dynamic positioning[D]. Trondheim: Norwegian University of Science and Technology,2013.

[4]S∅RDALEN O J. Optimal Thrust Allocation for Marine Vessels[J]. Control Engineering Practice,1997,5(9):1223-1231.

[5]SHI Xiaocheng, WEI Yushi, NING Jipeng, et al. Constrained control allocation using cascading generalized inverse for dynamic positioning of ships[C]. China, Beijing, IEEE,2011:1636-1640.

[6]许林凯,徐海祥.快速转向推进器推力优化分配研究[J].海洋工程,2015,35(2):13-20.

[7]OPPENHEIMER M W. Control allocation for over-actuated systems[C]. Ancona, IEEE,2006:1-6.

Thrust Allocation of Dynamic Positioning Based on Cascading Generalized Inverse

XU Haixiang1,2)FU Haijun2)YIN Jinjun3)LONG Fei3)

(KeyLaboratoryofHighPerformanceShipTechnologyofMinistryofEducation,Wuhan430063,China)1)(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)2)(WuhanInstituteofMarineElectricPropulsion,Wuhan430064,China)3)

Abstract：An algorithm named cascading generalized inverse (CGI) is proposed in order to handle the phenomenon of thruster saturation that usually occurs when generalized inverse (GI) is used to solve thrust allocation for dynamic positioning. This algorithm ensures that thrust and angle are in feasible area by cutting off saturated thrust and saturated angle. The simulation results show that thrust saturation and angle saturation phenomena have been avoided efficiently.

Key words：dynamic positioning; thrust allocation; saturation handling; cascading generalized inverse

doi:10.3963/j.issn.2095-3844.2016.02.002

中图法分类号：U662.9

收稿日期：2015-10-21

徐海祥(1975- )：男，博士，教授，主要研究领域为海洋动力定位系统开发

*国家自然科学基金项目(61301279)、船舶动力定位推力优化分配算法研究项目(2015-zy-002)资助