自密实混凝土对核电结构模块侧压力的数值分析研究

赵建忠，武伟

（国核工程有限公司，上海 200233）

自密实混凝土对核电结构模块侧压力的数值分析研究

赵建忠，武伟

（国核工程有限公司，上海 200233）

自密实混凝土具有很高的流动性，在A P1000结构模块墙体中应用较广。根据结构模块的结构特点建立计算模型，通过数值模拟分析自密实混凝土在结构模块浇筑过程中的应变、位移特性，分析提出了自密实混凝土对结构模块钢板的侧压力特点，可为其他类似项目结构模块的自密实混凝土施工提供参考。

自密实混凝土;结构模块;侧压力;数值分析

【DOI】10.13616/j.cnki.gcjsysj.2016.09.002

1 引言

自密实混凝土是一种具有高流动度且不离析、不泌水，能在免振捣的情况下，完全依靠自身重力作用，充满模板内空间，达到充分密实和获得最佳性能的混凝土。自密实混凝土区别于普通混凝土的最大特点在于其以流动性、黏聚性、通过性、抗离析性为主的工作性能，在核电土建施工中应用较多。自密实混凝土的高流动性也在一定程度上影响着钢结构模块的侧压力，为保险起见，多假定自密实混凝土浇筑过程中产生的侧压力近似于液体压力，这就极大地限制了自密实混凝土的浇筑速度，增加了浇筑施工的工作量和施工难度，对现场施工进度造成较大影响。

显而易见，自密实混凝土和纯液体是有很大区别的，因此针对于自密实混凝土在浇筑过程中产生的侧压力的研究是非常有必要的。本文结合AP1000核电结构特点，通过建立模型，数值分析自密实混凝土在结构模块浇筑过程中的应变、位移特性。

2 建立分析模型

根据结构模块墙体的结构特点，针对AP1000模块具体结构形式，选取典型墙体作为研究对象来进行分析。分析模型尺寸为762mm×5 000mm×10 500mm，4面由14mm厚的钢板围成；前后2个面的钢板分别对称布置有6根加劲肋，间隔为762mm，截面为L100mm×80mm×10mm；前后面上正对的加劲肋用C14b的槽钢连接，竖向间隔1219mm。钢板、角钢、槽钢的材质均为Q235B，底部可视为刚性支座，如图1所示。通过有限元软件对结构模块试验模型的“混凝土浇筑”的过程进行数值模拟，分析模块钢板墙体侧压力及侧向变形特征。

图1 数值模型平剖面示意图

3 数值分析计算

3.1 单次连续浇筑10m高时的侧压力

自密实混凝土在结构模块的侧压力分布特点目前还未得到有效研究，本次模拟主要目的是在不控制未初凝浇筑高度下研究侧压力分布特点，以便在结构安全条件下寻求最大浇筑高度，以提高施工效率。因此，在开始浇筑试验之前，需对模型结构的承受能力加以研究：假设一次性浇筑10m高自密实混凝土进行分析计算。

由于自密实混凝土设计尚缺乏统一的国家标准，所以在有关行业规范如《自密实混凝土设计与施工指南》（CCES02—2004）[1]、《自密实混凝土应用技术规程》（JGJ/T283—2012）[2]的基础上，参考国外相关规范如《TheEuropeanGuidelinesfor Self-CompactingConcrete》以及其他参考文献等，认为最不利工况是在一次性浇筑之后，混凝土尚未开始凝结时，对模板产生的侧压力最大，并接近于液压。故在用有限元进行计算时，仍可采用液压作为对钢板的侧压力，压力（kPa）沿高度的分布按公式p=ρ混凝土g（10-h）计算，其中ρ混凝土=2.4×103kg/m3，g=10m/s2，0≤h≤10m。侧压力分布曲线见图2。

图2 混凝土侧压力分布曲线

3.1.1 数值计算结果

对上述10mSCC一次性浇筑的工况分别采用2种有限元计算软件进行计算，发现中间位置的水平应变变化与侧压力分布呈正相关，但由于受到槽钢水平拉力的影响，曲线呈现出波浪形。2种软件的计算结果都反映了这一趋势。

根据图3，对10m自密实混凝土一次性浇筑的工况进行计算，发现中间位置的水平应变变化与侧压力分布呈正相关，但由于受到槽钢水平拉力的影响，曲线呈现出波浪形。2种软件的计算结果都反映了这一趋势。

图3 中间位置水平应变沿高度变化曲线

根据上图4，中间位置的竖向应变比水平应变小很多，除了第一点外，计算的应变值基本不超过500με。由于槽钢横向拉力的影响，曲线在-200με～500με内来回波动，并且绝对值随高度增加（侧压力减小）而减小。

图4 中间位置竖向应变沿高度变化曲线

由图5可知，中间位置垂直于钢板表面的水平位移沿高度呈减小的趋势，与侧压力的变化趋势一致，但由于受到槽钢水平拉力的影响，曲线呈波浪形。计算所得的中间位置最大位移分别为7.00mm左右。

图5 中间位置位移沿高度变化曲线

根据计算结果，板上最大主应力为420MPa左右，为拉应力，发生在钢板内侧槽钢所在的位置。Q235的屈服强度为235MPa，极限抗拉强度在370～500MPa范围内。显然，板上拉应力超过了屈服强度，会引起钢材的塑性变形甚至破坏。

综上所述，对于单次浇筑10m混凝土的工况，结构仍有可能发生破坏，形式主要为在钢板内侧，靠近槽钢的位置，因拉应力过大而产生屈服甚至被拉裂。因此，出于施工安全的考虑，实际上向模型一次浇筑10m混凝土是不可行的。

3.1.2 最大浇筑高度的确定

根据以上强度验算的结果，可以认为只要钢板上最大主应力小于Q235钢的强度设计值，则结构基本上是安全的。采用“试算法”求解混凝土的最大浇筑高度。

当h=5m，最大主应力为185.5MPa＜215MPa；当h=5.5m，最大主应力为213.4MPa＜215MPa；

考虑一定的安全裕度，建议一次性浇筑的最大高度不超过5.0m。

3.2 分层连续浇筑5.4m高时的侧压力

由于软件一主应力计算结果比软件二结果大，出于安全考虑，采用软件一进行模拟计算。根据侧压力限值（50kPa），在假设为全液压的状态下，自密实混凝土单次浇筑高度为2.1m左右。为研究在超过2.1m浇筑高度的情况下，模块钢板的应力应变特点。

以1.8m一层进行分层浇筑（本次数值分析假定单次浇筑高度为5.4m），浇筑速度为1.8m/h，则最大压力为43.2kPa。取残余应变约为最大应变的1/3左右，因此取相应的应力为15kPa。此外,对于某一层上部的点，其应变明显受到后一层混凝土的影响。综合考虑上述条件，以浇筑3层的情况为例，提出如下侧压力分布图，详见图6。

图6 混凝土侧压力分布图

采用通用有限元软件，计算混凝土浇筑过程中结构模块钢板墙体的应变和变形特点，在假设侧压力分布条件下，计算实体分层浇筑的墙体变形。由于计算量较大，本文仅以具有代表性的1层、2层、3层浇筑的工况为例，进行计算。

计算模型中间部位的水平应变在1层、2层、3层连续浇筑的工况下变化情况如图7所示。

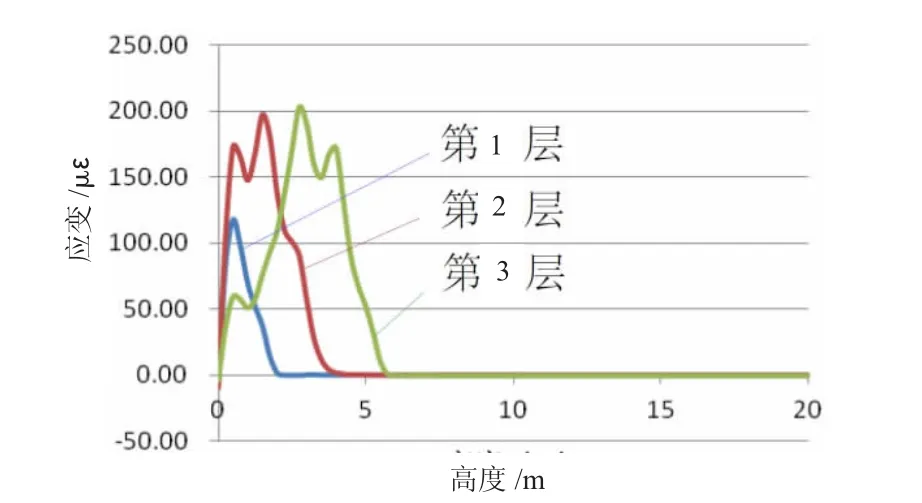
图7 模型前3层浇筑应变增长情况

从图7可以看出，在上述侧压力分布条件下，通过模型计算得到的最大应变为200με，同时肋部负应变的绝对值要大于肋间部位的正应变值。

采用模型分别在不同工况下计算5m高度范围内节点位移随高度的变化情况见图8。

图8 模型前3层浇筑位移增长情况

由图8可知，在上述侧压力分布条件下，在第1层1.8m浇筑过程中，在1m高附近，其位移达到最大值约0.85mm，在第2层1.8m浇筑过程中，同样在1m高附近，其位移达到最大值约1.7mm，之后随着第3层1.8m的浇筑，前2层自密实混凝土逐渐凝固收缩，位移开始减少，过程中，高度2.5m及3.5m处的位移先后达到阶段性峰值1.4mm和1.6mm。随着混凝土凝固收缩，各点位移逐渐减少。

在自密实混凝土的连续浇筑过程中，峰值分布形态略有差异，但位移从逐渐增加到逐渐减少的形态，可以判断结构整体处于弹性变形状态。

4 结构模块墙体的抗侧压力特点

在对模型自密实混凝土浇筑试验的模拟中，一次性浇筑10m混凝土时所产生最大水平应变在700～800με，肋部绝对值最大的负应变为-1300～-1600με左右，最大位移为6～8mm，钢板肋部最大主应力为440MPa，超出了屈服强度，接近极限抗拉强度，可能会引起结构破坏。试算结果表明：一次性浇筑的最大高度不宜超过5.0m。

而在连续浇筑5.0m的情况下（浇筑速度不超过1.8m/h），对模块墙体的承受能力进行数值分析研究，研究表明：

1）本次浇筑数值分析中，结构模型整体上处于弹性变形状态；

2）总体上看，侧压力随时间经历一个“迅速增长→缓慢衰减→稳定”的过程，峰值受浇筑高度和浇筑速率的影响，其衰减程度除了受浇筑高度和速率影响外，还与材料特性等密切相关，侧压力在后期保持一定稳定；

3）钢板水平应变随时间的变化形式在浇筑阶段及之后一段时间与侧压力很相似，总体变化范围在可控范围内；

4）位移变化形式也与侧压力类似，但变化幅度较小，后期同样比较稳定；

5）通过本次模型试验及对实测数据分析，只要合理地控制每次浇筑厚度和间隔时间，结构模块的连续浇筑是能够实现的；

6）结合数值计算结果，如果一次性浇筑，单次浇筑高度不超过5.0m时，且浇筑速度不超过1.8m/h时，模块墙体钢板的最大应变在3.5～4.0m之间，约200με，模块墙体钢板的最大位移在3.5m左右，约1.7mm。

5 结论

通过数值分析研究，自密实混凝土对结构模块钢板的侧压力大，在控制单次浇筑高度的情况下，钢板整体上处于弹性变形状态，侧压力随时间经历一个“迅速增长—缓慢衰减—稳定”的过程，峰值受浇筑高度和浇筑速率的影响，钢板水平应变和位移变化随时间的变化形式在浇筑阶段及之后一段时间与侧压力很相似，后期同样比较稳定，总体变化范围在可控范围内。

总体上看，数值计算得到的钢板墙的应力应变特性能在一定程度上反映钢板墙在自密实混凝土浇筑情况下的应力应变特征，有一定的合理性，但同时也应注意到数值计算中某些条件的简化会带来一定误差，尚需根据实际情况进行适当修正，尤其是应该进一步采用实体浇筑检测进行进一步分析。

【1】CECS02——2004自密实混凝土设计与施工指南[S].

【2】JGJ/T 283—2012自密实混凝土应用技术规程[S].

Numerical Analysis of Lateral Pressure on Nuclear Power Structural Module of Self-compacting Concrete

ZHAO Jian-zhong，WU Wei
（StateNuclearPowerEngineeringCompany，Shanghai200233，China）

With very high fluidity, self-compacting concrete is widely used in AP1000 Nuclear structure module wall.According to the structural characteristics of the module structure, calculation model is established. Through the numerical simulation analysis of self-compacting concrete in the process of pouring, strain and displacement characteristics ofmodule structure is simulated, and lateral pressure characteristics of self-compacting concrete bringing to bear on module steel structuresideisputforward.whichcanprovidethereferencefortheothersimilarprojectsconstruction.

self-compactingconcrete;structuremodule;lateralpressure;numericalsimulationanalysis

TU528.59

A

1007-9467（2016）09-0026-04

2016-03-10

赵建忠（1969～），男，浙江杭州人，高级工程师，从事AP系列核电厂项目工程管理与研究，（电子信箱）wuwei_china@163.com。