混合基于行和7/5提升格式的小波变换算法

蔡昭权

(惠州学院科研处, 广东 惠州 516007)

混合基于行和7/5提升格式的小波变换算法

蔡昭权

(惠州学院科研处, 广东 惠州 516007)

针对传统小波变换算法对内存需求大和计算复杂度高的问题，提出了混合基于行和7/5提升格式的小波变换算法。该算法采用基于行的小波变换，减少图像压缩的存储容量，利用BT7/5滤波器实现提升格式以减小计算复杂度。实验结果表明，该算法具有与JPEG2000相近的压缩效果，比传统的小波变换算法具有更小的内存需求，比其他基于行的提升小波算法具有更低的计算复杂度。

图像压缩；基于行的小波变换；提升格式

由于离散小波变换(简称DWT)具有较好的压缩能力，所以离散小波变换被广泛地应用于图像压缩领域[1-3]。在许多实际应用如遥感图像和医学图像处理中，数据量相当大以致于对内存的需求也相当之巨大，这就导致了传统小波变换有点力不从心，因此Chrysafis等[4]提出了基于行的小波变换。该变换方法采用逐行方式进行小波变换并输出小波系数，即只要缓存读入满足一定要求的行数，就开始进行小波变换，而不是要等待所有的数据全部读入缓存才开始进行小波变换，这种方法可以明显地减少小波变换所需要的内存容量。

自基于行的小波变换提出后，引起了国内外针对该算法的各种研究。刘正光等[5]将基于行的小波变换应用于图像压缩中，采用基于行的小波变换进行编码，用改进的提升格式代替Mallat算法进行小波变换；张宏伟等[6]提出采用三项加法单元形式的提升格式代替Mallat算法进行小波变换；Ye等[7]提出采用基于行的小波变换来处理JPEG2000中独立块编码问题；Eristi[8]提出了基于行的小波变换的电力容错诊断系统。

提升格式对于小变换的实现起着重要的作用，杨汉生等[9]提出了一种基于正交多项式的自适应提升格式来实现图像压缩；Shoba等[10]将基于提升格式实现的小波变换应用于卫星图像压缩中；高东等[11]利用基于提升格式的小波变换提出了一种过程数据在线去噪方法。

目前，在大部分基于提升格式的小波变换方法中，都是采用CDF9/7滤波器来实现的。由于基于9/7提升格式的小波变换的输出系数是无理数，而无理数在计算方面明显比有理数更为复杂。为了降低小波变换的计算复杂度和减少内存需求，同时又能够保证图像的压缩质量，本文尝试采用BT7/5滤波器实现7/5提升格式的小波变换以达到在变换过程减小计算复杂度的目的。

1 基于行的小波变换

与传统的小波变换方法不同，基于行的小波变换方法先逐行读取数据到缓存中，然后对行数据进行小波变换，当缓存中的行数达到由滤波器长度规定的数量后，才开始对列数据进行小波变换，而不是等待所有行的数据都读入到缓存后才对所有行进行小波变换的。在完成行的小波变换后就立刻输出小波系数，即逐行变换，逐行输出，直到所有的小波系数全部输出后才结束[4]。这样做的优势就在于：不用同时读入所有的数据行，以致于可以在很大程度上减少了内存的需求。

基于行的小波变换流程如下[4]：

设L=2α+φ为反馈分析滤波器的最大长度，L为奇数或是偶数由φ=1还是φ=0决定。一般地，以L为奇数为例(偶数情况可以类似处理)，设缓冲区的容量BFL等于滤波器的长度L。在边界处理方面，采用左延拓方式[12]。

对于第一级小波变换，首先图像数据写入到缓冲区BF1中，在写入的同时，也从BF1读取α+1行数据并进行行向小波变换。然后进行左延拓，在左延拓之后，如果BF1写满，则对第0行数据进行列向滤波，并输出低通结果。之后再读取一行新数据，同时对第1行数据进行列向滤波，并保存高通结果。与输出的低通结果不同的是，高通结果是先要暂存在一个同步缓冲区中，待所有级的小波变换完成之后一起输出。如此循环，则交替输出低通和高通结果。

对于第二级小波变换，把一级小波变换的低通结果写入缓冲区BF2中，之后与一级小波变换一样，先从BF2读取行数据进行行向小波变换，再进行列向小波变换。同理，又将交替输出低通和高通结果。

对于第N级小波变换，仍然类似地进行。此时可以计算出缓冲区的容量为

BF=N(2α+1)=NL

(1)

此外，设同步缓冲区的小为α(2N-i-1)，其中i=0,1,…,N-1为当前变换层。

综上所述，完成N级小波变换需要总的缓冲区容量为

(2)

2 提升格式

提升格式是实现小波变换最有效的方法[13]，设x[m,n]为一个2维信号源，信号源先进行行向小波变换再进行列向小波变换。一般情况下，提升格式主要包括分裂、预测和更新三个步骤。

1)分裂。

将信号源x[m,n]分解成奇数子集xo[m,n]和偶数子集xe[m,n]，其中xo[m,n]=x[2m+1,n]，xe[m,n]=x[2m,n]。

2)预测。

用偶数子集xe[m,n]预测奇数子集xo[m,n]，此时设P(·)为预测算子，则：

(3)

其中pi为高通滤波系数，由于预测而产生的预测误差可由下式表示：

d[m,n]=xo[m,n]+P(xe)[m,n]

(4)

3)更新。

通过预测误差d[m,n]来校正偶数子集xe[m,n]，其公式为

c[m,n]=xe[m,n]+U(d)[m,n]

(5)

其中U(·)为更新算子，U(·)可以通过下式计算：

(6)

其中uj为低通滤波系数。

因此，通过公式(4)和公式(5)，就可以用d[m,n]、c[m,n]和算子P(·)、U(·)表示信号源x[m,n]。

图1显示了采用提升格式的小波变换过程。

图1 采用提升格式的小波变换Fig.1 Wavelet transform using lifting scheme

2 基于行和7/5提升格式的小波变换算法

2.1 7/5提升格式

目前，大部分的小波变换算法都是采用CDF9/7滤波器实现提升格式，然而正如前文所说，CDF9/7的提升格式计算复杂度高，严重影响了计算效率[14]。由于BT7/5滤波器的小波系数是有理数，具有更低计算复杂度和更容易实现的特点，所以本文采用该滤波器代替CDF9/7滤波器实现小波变换算法中的提升格式。

假设低通分析滤波器用Hn(ξ)表示，低通综合滤波器用Gn(ξ)表示，具体如下：

(7)

(8)

同理，假设高通分析滤波器用Hn+1(ξ)表示，高通综合滤波器用Gn+1(ξ)表示，具体为：

(9)

(10)

令7/5小波基的提升参数α=t2，β=t3，γ=t4，θ=s3，由于欧几里德算法具有因式分解的功能，所以利用欧几里德算法在BT7/5滤波器中可以求出其多相矩阵。根据BT7/5滤波器的多相矩阵和系数的归一化条件可求出如下小波系数：

H0=(1+2βγ)θ

H1=[(2αβ+1)γ+α(1+βγ)]θ

H2=βγθ

G0=(2αβ+1)/(2θ)

G1=-β(2θ)

G2=αβ(2θ)

2.2 算法描述

基于行和7/5提升格式的小波变换算法就是结合基于行的小波变换思想，采用7/5提升格式实现小波变换。使用三项加法单元实现7/5提升格式，具体如下：

Routput=R1+c(R0+R2)

(11)

其中R0、R1和R2为输入缓冲区，Routput为输出缓冲区，c为乘法算子。

综上所述，算法的伪码如下：

∥R0、R1、R2代表输入缓冲区；R3、R4、R5和R6为输出缓冲区；R7和R8为同步缓冲区；p1、u1、p2和u2为三项加法单元的系数，分别对应BT7/5滤波器中的α、β、γ、θ，L为滤波器的长度。OH表示高通输出，OL表示低通输出。

读取第i行图像数据;

while (i不是最后一行) {

if (L为奇数)

{

R0=i/L;

R2=i/L;

R3=R1+p1(R0+R2);

R4=R5+u1(R1+R3);

R8=R6+p2(R5+R4);

OH=R8;

OL=R7+u2(R6+R8);

}

else

{

R0=i/L;

R1=i/L;

R5=R2+p1(R0+R1);

R6=R3+u1(R2+R5);

R7=R4+p2(R3+R6);

OH=R7;

OL=R8+u2(R4+R7);

}

读取第i行图像数据;

}

3 实验结果与分析

我们采用Visual C++编程软件在Windows 7操作系统环境下对本文算法(简称7/5LWT)进行了实现，硬件环境为Inter Core2 Quad CPU 2.83 Hz，内存为4.00 GB。为了证明本文算法的优势，本文算法也与目前比较流行的图像压缩算法Improved SPIHT[15]、Line-based BCWT和JPEG2000等进行了比较[7,14]。

3.1 压缩效果比较

我们对512×512的8 bpp(bits per pixel)的Lena图像进行图像压缩，测试了PSNR和MSE性能。所有比较的算法在编码量化方式上，使用嵌入零树编码。图2显示了PSNR的测试结果，图3显示了MSE的测试结果。

从图2中可以看出，在PSNR方面，7/5LWT算法稍微优于Improved SPIHT和Line-based BCWT算法，基本上与JPEG2000接近。图3中的实验数据也得到了类似的结果，这说明无论是在PSNR方面，还是在MSE方面，7/5LWT算法都能取得较好的压缩效果。由于Improved SPIHT和Line-based BCWT算法都是采用的CDF9/7提升格式，所以我们可以推测出一个这样的结论：基于7/5提升格式的小波变换在性能上并不会比基于CDF9/7提升格式的小波变换差，甚至会稍好一些。

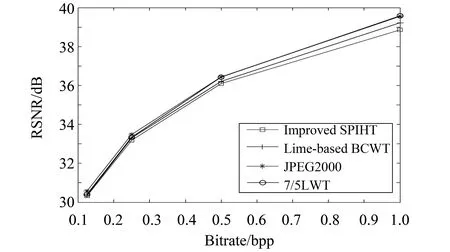
图2 不同比特率下PSNR性能Fig.2 Performance PSNR under different bit rate

图3 不同比特率下MSE性能Fig.3 Performance MSE under different bit rate

3.2 计算复杂度比较

为了进一步说明本文算法的优势，在相同缓冲区容量的条件下，我们对这4个算法在计算量方面进行了实验对比，一般地，算法的计算复杂度通过执行时间体现，图4显示了这4个算法的执行时间。从图4可以看出，7/5LWT算法的执行时间比JPEG2000要少一半以上。即使与Improved SPIHT和Line-based BCWT算法相比，7/5LWT算法的执行时间也它们要低一些，这也与前文的分析结果是一致的。

图4 不同比特率下的计算量Fig.4 Computation under different bit rate

4 结 论

为了找出一种既对内存需求少，又能保证图像压缩质量的小波变换算法，采用基于行的小波变换技术，结合BT7/5滤波器的提升方案，提出了一种混合基于行和7/5提升格式的小波变换算法。该算法采用基于行的小波变换降低内存需求，采用7/5提升格式提高计算速度。实验结果表明：通过与目前比较流行的图像压缩算法Improved SPIHT、 Line-based BCWT 和JPEG2000等的比较，本文算法具有更好的压缩性能和更少的计算复杂度。该算法能够较好地应用于存储容量有限的领域，如视频监控等。

[1] 柳薇, 陈冬丽. 基于多小波变换的图像编码算法研究[J]. 中山大学学报( 自然科学版), 2011, 50(5): 50-53.

[2] 郭昌. 小波变换与HMT 模型的图像插值算法[J]. 中山大学学报( 自然科学版), 2012, 51(3): 55-59.

[3] VENKATESHWAR R M. BHAGYA R V. Image resolution enhancement technique using lifting wavelet and discrete wavelet transforms[C]∥ Proceeding of the 3rd International Conference on Innovations in Computer Science and Engineering, 2015, 413: 235-239.

[4] CHRYSAFIS C, ORTEGA A. Line-based, reduced memory, wavelet image compression [J]. IEEE Transactions on Image Processing, 2000, 9(3): 378-389.

[5] 刘正光, 申旭刚. 基于行的小波变换及其在图像压缩中的应用[J]. 中国图像图形学报, 2004, 9(3): 370-374.

[6] 张宏伟, 刘正光, 陈红新. 应用提升格式实现的基于行小波变换的图像压缩算法[J]. 计算机应用, 2005, 25(7): 1626-1628.

[7] YE L, GUO J, NUTTER B, et al. Low-memory-usage image coding with line-based wavelet transform [J]. Optical Engineering, 2011, 50(2): 1-11.

[8] ERISTI H. Fault diagnosis system for series compensated transmission line based on wavelet transform and adaptive neuro-fuzzy inference system [J]. Measurement, 2013, 46(1): 393-401.

[9] 杨汉生, 孔鲲鹏, 许磊. 基于正交多项式的自适应提升格式[J]. 南京理工大学学报(自然科学版),2009, 33(3): 307-311.

[10] SHOBA P, MARIA L L, MOHAN V, et al. Landsat image compression using lifting scheme [C]∥ Proceeding of International Conference on Communications and Signal Processing (ICCSP). Tamilnadu Melmaruvathur, India, 2014: 1963-1968.

[11] 高东, 张贝克, 吴重光. 基于提升格式的过程数据在线去噪方法及其应用[J]. 计算机应用研究,2008, 25(10): 3198-3200.

[12] ZHANG L, QIU B. Edge-preserving image compression using adaptive lifting wavelet transform [J]. International Journal of Electronic, 2015, 102(7): 1190-1203.

[13] GUO F, LIU X, ZHAO C. The image enhancement technology based on lifting wavelet [J]. Applied Mechanics and Materials, 2014, 513/514/515/516/517: 3261-3264.

[14] ZENG W, DALY S, LEI S. An overview of the visual optimization tools in JPEG 2000 [J]. Signal Processing: Image Communication, 2002, 17(1): 85-104.

[15] 丁晓峰, 何凯霖. 基于改进提升小波变换 SPIHT 的图像压缩算法[J]. 计算机测量与控制, 2014, 22(11): 3670-3672.

Hybrid line-based 7/5 lifting scheme wavelet transform algorithm

CAI Zhaoquan

(Scientific Research Office, Huizhou University, Huizhou 516007, China)

In view of the problem of big memory requirement and high computational complexity in the traditional wavelet transform algorithm, a hybrid line-based 7/5 lifting scheme wavelet transform algorithm is proposed. In the proposed algorithm, the line-based wavelet transform is used to reduce requirement of buffer in image compression, and the lifting scheme which is implemented by BT7/5 filter is used to reduce computation complex. The experimental results show that the proposed algorithm has similar the quality of compression with JPEG2000 and requires smaller memory than the traditional wavelet transform algorithm. Meanwhile, the proposed algorithm has lower computational complexity than the lines-based wavelet algorithm variant.

image compression; line-based wavelet transforms; lifting scheme

10.13471/j.cnki.acta.snus.2016.05.010

2016-01-08

国家自然科学基金资助项目(61170193, 61370185)； 广东省自然科学基金资助项目(S2013010013432)； 广东省自然科学基金重点资助项目(S2012020011081)

蔡昭权(1970年生), 男；研究方向: 图像处理，模式识别;E-mail:cai@hzu.edu.cn

TN919.81

A

0529-6579(2016)05-0052-05