一类分数阶哈密顿系统非平凡解的存在性

程 伟，徐家发

(重庆师范大学数学科学学院，重庆 401331)

一类分数阶哈密顿系统非平凡解的存在性

程 伟，徐家发

(重庆师范大学数学科学学院，重庆 401331)

利用变化的喷泉定理，研究了一类分数阶哈密顿系统。构造合适的工作空间和变分结构，在非线性项超二次增长的情形下获得该系统非平凡解的存在性，相关结论推广和改进了某些已有的结果。

分数阶哈密顿系统；喷泉定理；非平凡解

本文主要研究以下分数阶哈密顿系统非平凡解的存在性:

u∈Hα(R,RN)

(1)

其中α∈(1/2,1),t∈R,u∈RN,W∈C1(R×RN,R)，▽W是W关于u的梯度。关于L(t), 我们始终假设以下条件成立：

∀t∈R,u∈RN

近年来，对于分数阶问题的研究越来越受到人们的青睐，数学家们研究发现用新的分数阶模型能更精确地模拟现实问题。分数阶微分方程非常适合用来描述现实生活中具有记忆和遗传特性的问题，如：分形和多孔介质中的弥散、电容理论、电解化学、半导体物理、湍流、凝聚态物理、粘弹性理论、生物数学及统计力学等等，因此研究这类方程解的性质有理论和现实意义。在文[1]中, 作者列举了大量分数阶模型在实际问题中的应用。例如电化学模型，Caputo在讨论电化学的可极化介质时，提出电场E和电流密度D之间关系的分数阶模型，一维的情形为

γD(v)+αD=σE+δE(v)

其中γ,α,σ,δ皆为常数,D(v)=DvD,E(v)=DvE,ν是实数。运用变分方法和临界点理论研究分数阶问题是比较新的课题, 近期有很多学者致力于这方面的工作, 参见文献[2-9]及其所附参考文献。

在文[2]中, Torres运用山路定理研究了问题(1)非平凡解的存在性,其中W满足著名的Ambrosetti-Rabinowitz条件：

(AR) 存在常数μ>2使得

0<μW(t,x)≤(x,▽W(t,x)),

∀(t,x)∈R×RN{0}

在文[3]中, 在W次二次增长的情形下, 作者运用亏格理论获得了问题(1)无穷多解的存在性。他们的具体条件是：

(FHS1) 对任意的t∈R,W(t,0)=0, 且

∀(t,x)∈R×RN

其中，1<ϑ<2，a:R→R+是一有界连续函数，b:R→R+是一连续函数且b∈L2/(2-ϑ)(R×R);

(FHS2) 存在常数1 <σ≤ϑ < 2 使得

(▽W(t,x),x)≤σW(t,x),
∀(t,x)∈R×RN{0}

(FHS3)W(t,x)=W(t,-x),

∀(t,x)∈R×RN。

在文[4]中, 在W次临界增长的情况下, 作者运用喷泉定理获得了问题(1)高能量解的存在性，并运用山路定理和Ekeland变分原理获得了带有扰动项的分数阶哈密顿系统至少两个非平凡解的存在性(N= 1)：

Wu(t,u(t))+g(t),u∈Hα(R×R)

(2)

受上述文献的启发,本文运用变化的喷泉定理研究问题(1)非平凡解的存在性,为此我们首先给出本文所使用的假设条件：

(H1)W∈C1(R×RN,R),且存在d1>0和p∈(2,+∞)使得

∀(t,x)∈R×RN

(H4) 存在d2>0,L>0 使得

定理1 若条件(H1)-(H4)和(FHS3)成立，则问题(1)至少存在一个非平凡解。

1 基础知识

首先介绍有关Liouville-Weyl分数阶的计算。α(0<α<1)阶Liouville-Weyl分数阶积分定义为:

(3)

和

(4)

由此可给出α(0<α<1)阶Liouvlle-Weyl分数阶导数的定义:

(5)

和

(6)

定义(5)-(6)式可以改写成以下形式

(7)

和

(8)

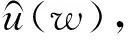
令u(x)是定义在R上的函数，经过傅里叶变换可以得到如下的等式：

(9)

(10)

以下构造问题(1)对应的变分结构，赋予Banach空间Lp(R,RN)(p∈[2,+∞) 的范数为

赋予Banach空间L∞(R,RN)的范数为

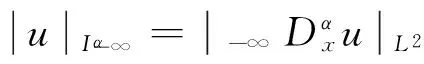
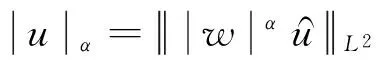
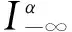
令

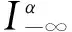
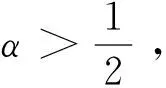
注1 根据引理1, 由于

则可得u∈Lq(R,RN)，∀q∈[2,+∞)，如果u∈Hα,α∈(1/2,1)。

记

Xα

(L(t)u(t),u(t))]dt<∞}

则Xα是一自反可分的Hilbert 空间，其上的内积为

(L(t)u(t),v(t))]dt

相对应的范数为

为方便，简记

引理2[2-3]若条件(L)成立，则Xα连续嵌入到Hα。

引理3[2-3]若条件(L)成立，则嵌入Xα→Lq(R,RN)(q∈[2,+∞))既是连续的又是紧的。

因此结合引理1，对任意的q∈[2,+∞]，存在Cq使得

(11)

考虑C1-泛函Φλ:X→R如下：

Φλ(u)=A(u)-λB(u),λ∈[1,2]

(12)

引理4[10](12)式所定义的泛函Φλ满足：

(C1) 对任意的λ∈[1,2]，Φλ映有界集为有界集，且

Φλ(u)=Φλ(-u),∀(λ,u)∈[1,2]×X;

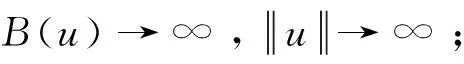
(C3) 存在rk>ρk>0使得

∀λ∈[1,2]

则

∀λ∈[1,2]

2 主要定理的证明

为了得到问题(1)弱解的存在性，在Xα上定义相应的能量泛函如下：

(13)

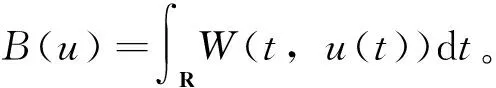
∀(t,u)∈R×RN

(14)

结合(11)式可知B和J都是良定义的。更进一步，记(Xα)*是Xα的对偶空间，根据文[11]中的引理1，若条件(L)和(H1)成立，则B∈C1(Xα,R),B′:Xα→(Xα)*是紧的，因而J∈C1(Xα,R)，且对任意的u,v∈Xα，有

▽W(t,u(t)),v(t))dt,

并由此可知，问题(1)的弱解就是能量泛函J的临界点。

对于j,k∈N,定义Xj显然且dimXj<∞,∀j∈N。

为了运用引理4来证明我们的结论，定义泛函A，B和Φλ如下：

引理5 若条件(L)，(H1)-(H2)成立，则存在ρk>0使得

证明 根据条件(H1)-(H2), 对于任意给定的ε>0, 存在Cε使得

∀(t,u)∈R×RN

结合(11)式，有

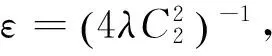
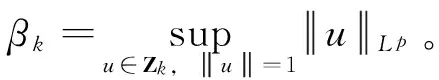
有

证毕。

引理6 若条件(L), (H1)-(H3)成立，则存在rk>0使得

证明 首先证明存在ε>0使得

∀u∈X{0},X⊂Xα,dimX<∞

(15)

否则对任意的n∈N,存在序列{un}∈X{0}使得

(16)

否则的话，

(17)

从而

(18)

对任意的n∈N，定义

以及

从而对足够大的n，有

meas(Λn∩Λ0)=

从而对足够大的n，

∀(t,u)∈R×RN

注意到dimYk<∞,所以

这是矛盾的。矛盾表明maxu∈Yk,‖u‖=rkΦ1(u)≤0。证毕。

(19)

∀k≥1,

∀n∈,k≥1

结合(19)式，有

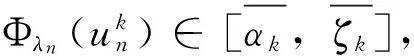
(20)

vn→v0弱收敛于Xα

(21)

vn→v0强收敛于Lq(R,RN),q∈[2,+∞)

(22)

vn(t)→v0(t)a.e.t∈R

(23)

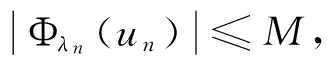
(24)

以下分两种情况讨论：

第一种情况：v0不恒等于0。

这与(24)式矛盾。

第二种情况:v0恒等于0。

根据(24)式，注意到λn→1，有

(25)

注意到条件(H2)，存在d5>0使得

∀

结合条件(H4)，有

▽W(t,x),x)-2W(t,x)]+d5,

∀(t,x)∈R×RN

从而由(22)-(23)式可知

这与(25)式矛盾。

[1] 郑祖庥. 分数微分方程的发展和应用[J]. 徐州师范大学学报(自然科学版), 2008, 26 (2): 1-10.

[2] TORRES C, Existence of solution for a class of fractional Hamiltonian systems [J]. arXiv: 1212. 5811v1, 2012.

[3] ZHANG Z, YUAN R. Variational approach to solutions for a class of fractional Hamiltonian systems [J]. Math Methods Appl Sci, 2014, 37(13): 1873-1883.

[4] XU J, O’REGAN D, ZHANG K. Multiple solutions for a class of fractional Hamiltonian systems [J]. Fract Calc Appl Anal, 2015,18 (1): 48-63.

[5] CHEN J, TANG X. Innitely many solutions for a class of fractional boundary value problem [J]. Bull Malays Math Sci Soc, 2013, 36(4): 1083-1097.

[6] NYAMORADI N, Innitely many solutions for a class of fractional boundary value problems with Dirichlet boundary conditions [J], Mediterr J Math, 2014, 11(1): 75-87.

[7] JIAO F, ZHOU Y. Existence of solutions for a class of fractional boundary value problems via critical point theory [J]. Comput Math Appl, 2011, 62(3): 1181-1199.

[8] GE B. Multiple solutions for a class of fractional boundary value problems [J]. Abstr Appl Anal, 2012, Article ID 468980.

[9] BAI C. Existence of three solutions for a nonlinear fractional boundary value problem via a critical points theorem [J]. Abstr Appl Anal, 2012, Article ID 963105.

[10] ZOU W M. Variant fountain theorems and their applications [J]. Manuscripta Math, 2001, 104(3): 343-358.

[11] YE Y W, TANG C L. Multiple solutions for Kirchhoff-type equations in RN[J]. J Math Phys, 2013, 54: Article ID 081508. http:∥dx.doi.org/10.1063/1.4819249

[12] WILLEM M. Minimax theorems [M]. Boston: Birkhauser, 1996.

Existence of nontrivial solutions for a class of fractional Hamiltonian systems

CHENG Wei,XU Jiafa

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

Using the variant fountain theorem, a class of fractional Hamiltonian systems are studied. With establishing appropriate work space and variational structure, the existence of nontrivial solutions for the superquadratic fractional Hamiltonian systems is obtained, and the obtained results extend and improve some known results.

fractional Hamiltonian systems; fountain theorem; nontrivial solutions

10.13471/j.cnki.acta.snus.2016.05.004

2016-03-16

国家自然科学基金资助项目(11371117)；重庆师范大学基金资助项目(15XLB011)

程伟(1985年生)，男；研究方向：拓扑动力系统，微分方程；通讯作者：徐家发;E-mail:xujiafa292@sina.com

O175.2

A

0529-6579(2016)05-0021-06