基于自适应TVp正则化图像恢复方法
李率杰,冯兆永
(1. 河南科技大学数学与统计学院,河南 洛阳 471023;2. 中山大学数学学院,广东 广州510275)
基于自适应TVp正则化图像恢复方法
李率杰1,冯兆永2
(1. 河南科技大学数学与统计学院,河南 洛阳 471023;2. 中山大学数学学院,广东 广州510275)
为了解决图像恢复时所引起的阶梯效应和边缘模糊问题,定义可变TVp范数,提出一个自适应TVp(Adaptive TVp, ATVp)正则恢复模型,并结合AOS数值计算方法,给出完整的ATVp正则恢复算法,其中p可以自动区分图像中的边缘和平坦区域,自适应选择不同的数值,使得新模型在恢复的同时不仅能够自适应的对图像中目标边缘进行有效的保护,而且可以避免出现阶梯效应。实验表明,和主要的一些正则模型相比,本恢复算法对模糊图像的恢复无论在视角效果还是定量指标上都有了明显的改进。
图像恢复;ATVp正则;AOS数值计算
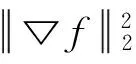
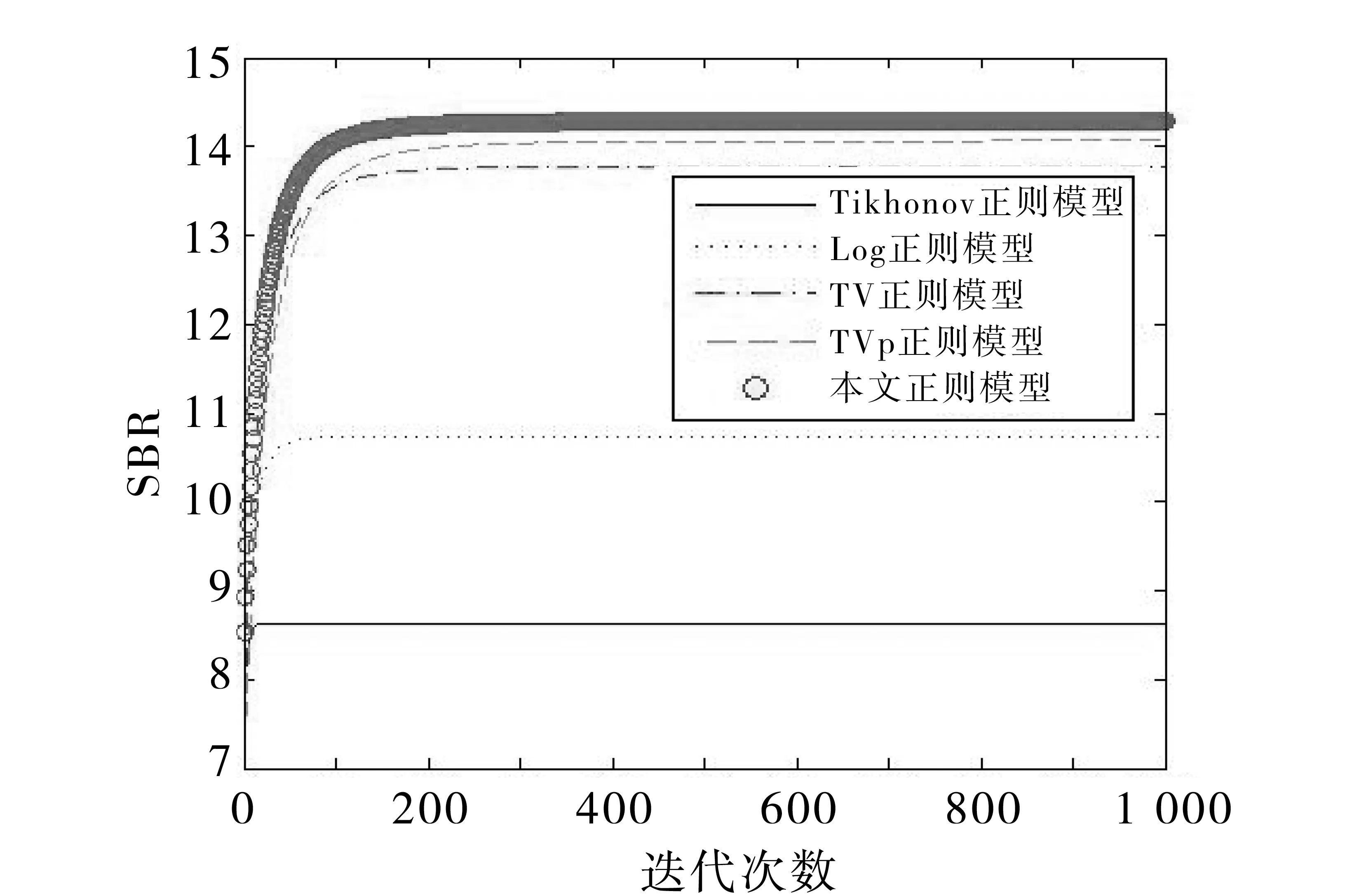
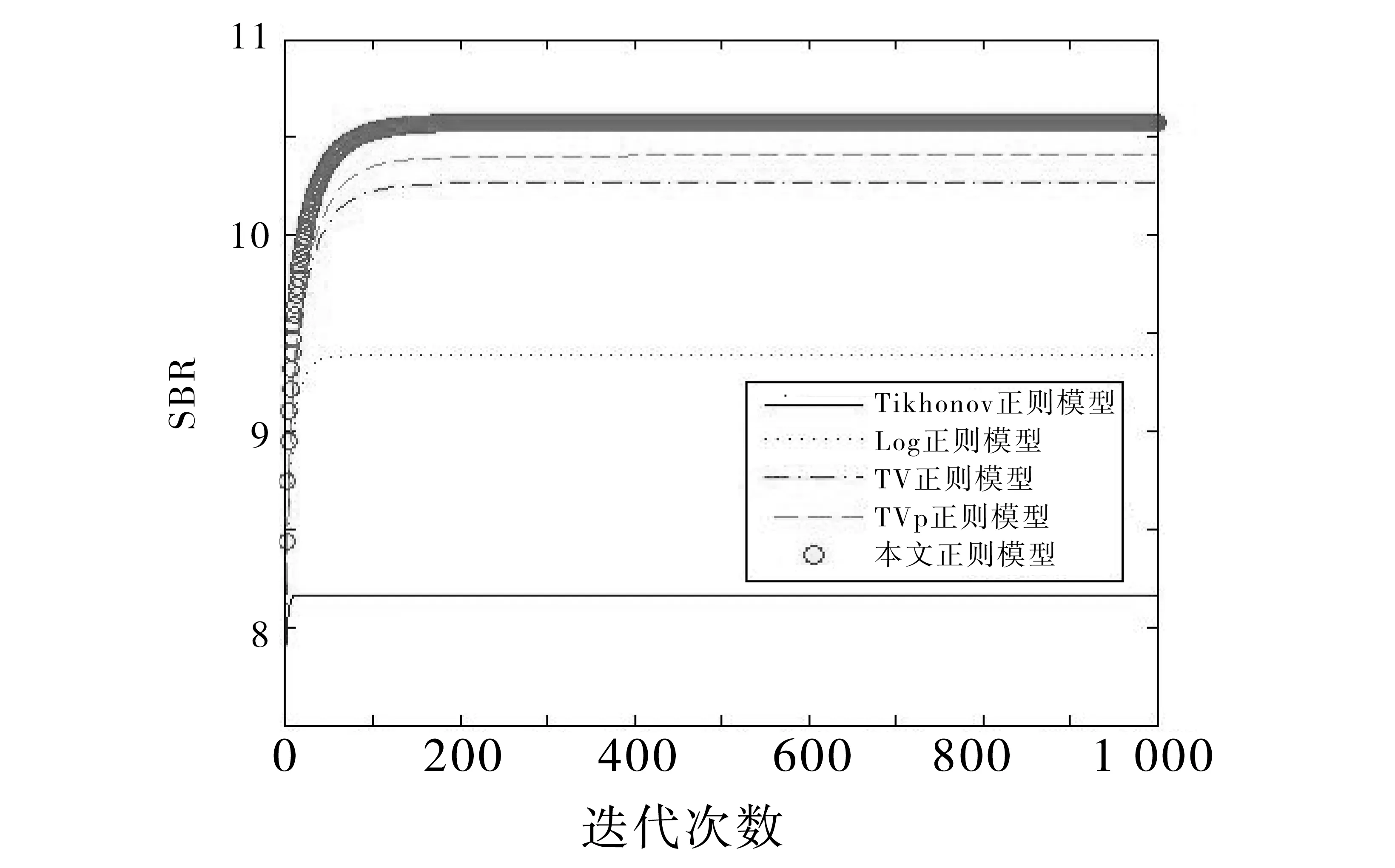
为了解决图像恢复中阶梯效应,本文提出了自适应TVp(AdaptiveTVp, ATVp)正则方法,其中,1 从数学意义上理解,图像恢复问题是一个病态的逆问题,其可总结为一个退化模型:f为定义在Ω⊂R2上的理想原图像,η为加入的加性高斯白噪声,观察到的待恢复图像g可表示为: g=Hf+η (1) 其中H为模糊算子矩阵。由于这是病态问题,因此图像恢复中需要对其正则化,在文献[1]中Tikhonov等提出以下能量泛函: (2) 其中 为l2范数,α为正常数,模型恢复将使得图像边缘模糊。Rudin等[2]提出了TV正则,TV正则因为其分片光滑性质,可以保持图像边缘,基于TV正则的图像恢复能量泛函为: (3) 为了在图像恢复的同时既能避免阶梯效应,又能更好的保护图像的边缘信息,本文提出ATVp正则方法,p可以根据图像特征自适应选取。其模型如下: (4) 其中 这里Gσ为高斯滤波,K>0为固定的参数,*为卷积符号。 为了求解模型,极小化能量泛函,得到恢复后的图像f,由变分法原理先对泛函求导可得Euler-Lagrange方程: (5) (6) 其中H*为H的共轭,方程(6)的解即为所求恢复后的图像f。 为了进一步说明本文提出的ATVp正则模型的优异的扩散能力,对方程(6)的正则项在图像局部结构上分解,然后进行分析其扩散方向和强度。在图像的局部定义直角坐标系(ξ,η),如图1所示,其中η-轴平行于梯度方向,ξ-轴垂直于梯度方向,即: 图1 坐标系(ξ,η)示意图Fig.1 Coordinate system(ξ,η) (7) 从上式可以看出,方程(6)本质上为非线性的各向异性扩散方程,其扩散能力由扩散系数 所控制,如图1所示。 这就意味着在图像目标边缘处沿梯度方向的扩散强度接近于零,几乎没有扩散,只沿着图像目标边缘的垂直于梯度的方向即切线方向进行扩散,从而可以保护图像目标边缘不被模糊,保持图像目标边缘信息。 这就意味着在沿梯度方向和切线方向的扩散强度接近于相等,在图像的平坦区域内沿着沿梯度和切线两个方向进行同等扩散,从而可以更好的光滑图像,去除噪声,避免出现阶梯状效应。 根据以上分析,本文提出的ATVp正则模型可以在图像恢复的同时避免TV正则模型的阶梯状效应和Tikhonov正则模型的模糊边界的缺点。 对于提出的ATVp正则模型的数值计算,关键是求解方程(6),在求解该方程时本文采用半隐格式的加性算子分裂(Additive Operator Splitting,AOS)算法[19-20],具体如下: 方程(6)可用半隐有限差分格式来逼近: f(i)-ταH*(Hf(i+1)-g) 其中τ表示时间步长,演化方程的求解将采用AOS算法,首先进行算子分裂,移项可得: 由AOS算法原理,上式的求解可通过: 从而可得f(i+1): AOS算法是绝对稳定的,从而可以在保证精度的前提下,选用尽可能大的时间步长以提高效率,并且时间步长的选定,不是出于稳定性考虑,而是出于精度和效率的折中考虑。 本节通过仿真实验来验证算法的有效性,选用一幅大小为256×256的著名的Lena图像进行实验,Lena图像细节丰富利于检验比较恢复结果。并将本文ATVp正则模型与Tikhonov正则模型[1],Log正则模型[14],TV正则模型[2],TVp正则模型(这里选定p=0.8)[16]分别对恢复运动、失焦和噪声引起的模糊进行了比较。为了更加客观,本文从视角效果与定量指标两方面对图像质量进行比较。采用的定量指标SBR(Signaltoblurringratio)用来定量模糊的程度,恢复的效果,采用PSNR(峰值信噪比)定量噪声的强度,去噪的效果,定义分别如下: 其中u表示原模糊前图像,unew表示恢复后图像,M,N分别为图像的行列数。容易看出SBR和PSNR的值越大说明图像恢复的质量越好。 实验1 验证算法对运动模糊图像恢复效果,如图2所示。本实验首先对原始的Lena图像加入角度θ=45°,运动距离为L=15像素的运动模糊,如图2(a)所示。令模型中的K=1,以下实验相同,并且试验发现算法对时间步长并不敏感,在τ=1附近算法都是稳定的,另外为了更接近原图像,权值α选的较大,本实验参数选择为:时间步长:τ=0.8,α=2.5。图2(b)-(f)为各模型恢复效果,容易看出Tikhonov正则与Log正则恢复的图像比较模糊,TV正则恢复的图像阶梯效应明显,TVp正则模型得到了稍微的改善,本文ATVp正则模型在改善阶梯效应,保持边缘上恢复效果更好。同时算法收敛方面也是较好(见图3),在迭代100次左右就达到了稳定,并且得到更高的SBR值如表1所示。 图2 Lena图像的运动模糊恢复结果Fig.2 Restored result of motion blurred Lena 模糊类型性能指标恢复前Tikhonov正则模型Log正则模型TV正则模型TVp正则模型本文ATVp正则模型运动模糊SBR7.31558.630110.737013.636014.065014.2807失焦模糊SBR7.33908.16389.384710.273110.411910.5790噪声PSNR20.048325.731626.090327.562627.744928.4431 图3 各模型对运动模糊恢复SBR值收敛曲线图Fig.3 SBR curves with iteration times in experiment 1 实验2验证算法对失焦模糊图像恢复效果,如图4所示。 图4 Lena图像失焦模糊恢复结果Fig.4 Restored result of out of focus for Lena 本实验对原始图像加入了模糊窗口h=21,标准差σ=5的Gaussian模糊,如图4(a)。参数同样选择为:时间步长:τ=0.8,λ=2.5,图4(b)-(f)为各模型恢复效果,从各恢复图可以看出,本文ATVp正则模型恢复的效果显然比其他正则模型更为理想。图5和表1也可以验证算法在运算收敛和指标SBR值方面表现良好。 图5 各模型对失焦模糊恢复SBR值收敛曲线图Fig.5 SBR curves with iteration times in experiment 2 实验3 本实验主要验证算法的去除噪声的效果,如图6所示。 图6 Lena图像噪声恢复结果Fig.6 Restored result of noisy Lena 本实验在原始图像加入了均值为零,方差为0.1的高斯噪声,如图6(a)。实验中选择时间步长τ=0.8,为了加强磨光作用,去除噪声,λ选择较小,λ=0.05。图6(b)-(f)为各模型恢复效果,结果正如实验1中分析,Tikhonov正则与Log正则恢复的图像边缘比较模糊,TV正则恢复的图像出现阶梯效应,TVp正则模型得到了稍微的改善,本文ATVp正则模型由于综合了Tikhonov正则和TV正则模型的优点,摒弃其缺点得到了较好效果,并且运算收敛理想(见图7),迭代50次左右就已达到稳定。PSNR值相比其他模型有了大幅提高,如图7和表1所示。 图7 各模型对噪声恢复PSNR值收敛曲线图Fig.7 PSNR curves with iteration times in experiment 3 为了解决算法在恢复图像时所引起的阶梯效应和边缘模糊问题,在本文中基于自适应TVp范数,提出一个ATVp正则模型, 并结合AOS数值计算方法,得到完整的ATVp正则恢复算法,通过分析,容易看出p可以自动区分图像中的边缘和平坦区域,从而自适应的选择不同的值,使得新模型可以实现在图像边缘处逼近TV正则模型来保持边缘,在图像平坦区域内逼近Tikhonov正则模型,可以充分磨光图像,从而不仅能够自适应的对图像中的边缘进行有效的保护,而且可以避免出现阶梯效应。 通过一系列实验表明,和主要的一些正则模型相比,本文恢复算法对模糊图像的恢复无论在视角效果还是定量指标都有了明显的改进。 [1]TIKHONOVAN,ARSENINVY.Solutionsofill-posedproblems[M].WashingtonDC:WinstonandSons, 1977. [2]RUDINL,OSHERS,FATEMIE.Nonlineartotalvariationbasednoiseremovalalgorithms[J].PhysicaD, 1992, 60(1/2/3/4): 259-268. [3]CHAMBOLLEA.Analgorithmfortotalvariationminimizationandapplications[J].JournalofMathematicalImagingandVision, 2004, 20(1): 89-97. [4]BECKA,TEBOULLEM.Fastgradient-basedalgorithmsforconstrainedtotalvariationimagedenoisinganddeblurringproblems[J].IEEETransactionsonImageProcessing, 2009, 18(11): 2419-2434. [5]WENYW,CHANRH.Parameterselectionfortotalvariationbasedimagerestorationusingdiscrepancyprinciple[J].IEEETransactionsonImageProcessing, 2012, 21(4): 1770-1781. [6]CHOTS,ZITNICKCL,JOSHIN,etal.Imagerestorationbymatchinggradientdistributions[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2012, 34(4): 683-694. [7]ALLARDWK.TotalvariationregularizationforimagedenoisingII,examples[J].SIAMJ.ImagingSciences, 2008, 1(4): 400-417. [8]ALLARDWK.TotalvariationregularizationforimagedenoisingIII,examples[J].SIAMJ.ImagingSciences, 2009, 2(2): 532-568. [9]WOHLBERGB,RODRIGUEZP.Aniterativelyreweightednormalgorithmforminimizationoftotalvariationfunctional[J].SignalProcessingLetters,IEEE, 2007, 14(12): 948-951. [10]CHENQ,MONTESINOSP,SUNQS,etal.Adaptivetotalvariationdenoisingbasedondifferencecurvature[J].ImageandVisionComputing, 2010, 28(3): 298-306. [11]LOUCHETC,MOISANL.Totalvariationasalocalfilter[J].SIAMJournalonImagingSciences, 2011, 4(2): 651-694. [12]HUY,JACOBM.Higherdegreetotalvariation(hdtv)regularizationforimagerecovery[J].IEEETransactionsonImageProcessing, 2012, 21(5): 2559-2571. [13]LEEYJ,LEES,YOONJ.Aframeworkformovingleastsquaresmethodwithtotalvariationminimizingregularization[J].JournalofMathematicalImagingandVision, 2014, 48(3): 566-582. [14]LISJ,YAOZA.Imageinpaintingalgorithmbasedonpartialdifferentialequationtechnique[J].Imagingsciencejournal,2013, 61(3): 292-300. [15]SUX.DeblurringbysolvingaTVpregularized optimization problem using split bregman method [J]. Advances in Multimedia, 2014(2014), Article ID 906464. doi:10.1155 /2014/906464. [16] YAN J, LU W S. Image denoising by generalized total variation regularization and least squares fidelity [J]. Multidimensional Systems and Signal Processing, 2015, 26(1): 243-266. [17] 李率杰,李鹏,冯兆永,等. 基于Navier-Stokes方程的图像修复算法[J]. 中山大学学报(自然科学版), 2012, 51(1): 9-13, 18. [18] 杨朝霞,逯峰,田芊芊. 自适应双正则参数法在图像恢复中的应用[J]. 中山大学学报(自然科学版), 2005, 44(4): 20-23, 27. [19] WEICKERT J, ROMENY B, VIERGEVER M. Efficient and reliable schemes for nonlinear diffusion filtering [J]. IEEE Transactions on Image Processing, 1998, 7(3): 398-410. [20] KUHNE G, WEICKERT J, VIERGEVER M. Fast implicit active contours models [J]. Pattern Recognition Lecture Notes on Computer Science, 2002, 2449: 133-140. Image restoration method based on adaptive TVpregularization LI Shuaijie1, FENG Zhaoyong2 (1.School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang 471023, China;2. School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China) In order to avoid the staircasing effect and edge blurring problem. A variable TVpnorm was defined, and an adaptive TVp(ATVp) regularization model was proposed. Combining the AOS numerical method, a complete ATVpregularization algorithm was shown, wherepcanbeadaptiveselectedaccordingtodifferentimageareas.Thecharacteristicsmakethenewmodelpreservetheedgeinformationbetterandavoidthestaircasingeffectwhileimagerestoration.Experimentsshowedthatcomparedwiththeexistingregularizationmodels,itimprovedtherestorationresultsinbothvisualeffectsandSBRandPSNR. image restoration; ATVpregularization; AOS method 10.13471/j.cnki.acta.snus.2016.05.002 2016-03-25 国家自然科学基金面上资助项目(11271381,11471339);国家自然科学基金青年基金资助项目(61301229);河南省教育厅资助项目(15A110020);河南科技大学博士科研启动基金资助项目(13480032);广州市科技计划资助项目(201607010144) 李率杰(1980年生),男;研究方向:偏微分方程,图像处理;通讯作者:冯兆永;E-mail:fzhaoy@mail.sysu.edu.cn TP911.73 A 0529-6579(2016)05-0008-061 Tikhonov正则与 TV正则模型
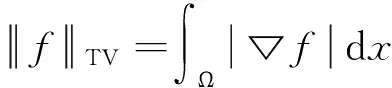
2 自适应TVp正则模型
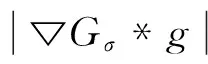


3 模型分析




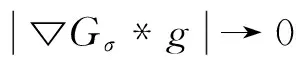
4 数值计算
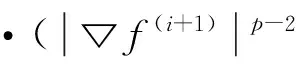
5 仿真实验





6 结 论

